Contractible space
From Encyclopedia of Mathematics
A topological space  that is homotopy equivalent (see Homotopy type) to a one-point space; i.e., if there is a point
that is homotopy equivalent (see Homotopy type) to a one-point space; i.e., if there is a point  and a homotopy from
and a homotopy from  to the unique mapping
to the unique mapping  . Such a mapping is called a contraction.
. Such a mapping is called a contraction.
The cone over  is contractible. For a pointed space
is contractible. For a pointed space  , the requirement for contractibility is that there is a base-point-preserving homotopy from
, the requirement for contractibility is that there is a base-point-preserving homotopy from  to the unique mapping
to the unique mapping  .
.
A space is contractible if and only if it is a retract of the mapping cylinder of any constant mappping  .
.
A set  is starlike with respect to
is starlike with respect to  if for any
if for any 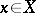 the segment
the segment  lies in
lies in  . Convex subsets and starlike subsets in
. Convex subsets and starlike subsets in  are contractible.
are contractible.
References
| [a1] | C.T.J. Dodson, P.E. Parker, "A user's guide to algebraic topology" , Kluwer Acad. Publ. (1997) |
| [a2] | E.H. Spanier, "Algebraic topology" , McGraw-Hill (1966) |
How to Cite This Entry:
Contractible space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Contractible_space&oldid=50240
Contractible space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Contractible_space&oldid=50240
This article was adapted from an original article by M. Hazewinkel (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article