Ricci theorem
From Encyclopedia of Mathematics
In order that a surface 
with metric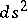 
and Gaussian curvature 
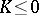be locally isometric to some minimal surface 
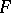it is necessary and sufficient that (at all points where 
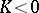) the metric 
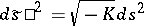be of Gaussian curvature 
.
There are generalizations [1], describing Riemannian metrics which arise as metrics of minimal submanifolds in Euclidean spaces of arbitrary dimension.
References
| [1] | S.-S. Chern, R. Osserman, "Remarks on the Riemannian metrics of a minimal submanifold" E. Looijenga (ed.) D. Siersma (ed.) F. Takens (ed.) , Geometry Symp. (Utrecht, 1980) , Lect. notes in math. , 894 , Springer (1981) pp. 49–90 |
How to Cite This Entry:
Ricci theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ricci_theorem&oldid=48538
Ricci theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ricci_theorem&oldid=48538
This article was adapted from an original article by I.Kh. Sabitov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article