Covariant
of a tensor 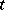 on a finite-dimensional vector space
on a finite-dimensional vector space 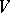
A mapping 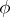 of the space
of the space 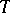 of tensors of a fixed type over
of tensors of a fixed type over 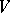 into a space
into a space 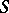 of covariant tensors over
of covariant tensors over 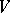 such that
such that  for any non-singular linear transformation
for any non-singular linear transformation 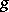 of
of 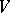 and any
and any 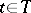 . This is the definition of the covariant of a tensor with respect to the general linear group
. This is the definition of the covariant of a tensor with respect to the general linear group 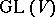 . If
. If 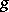 is not arbitrary but belongs to a fixed subgroup
is not arbitrary but belongs to a fixed subgroup 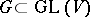 , then one obtains the definition of a covariant of a tensor relative to
, then one obtains the definition of a covariant of a tensor relative to 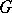 , or simply a covariant of
, or simply a covariant of  .
.
In coordinate language, a covariant of a tensor on a finite-dimensional vector space is a set of functions
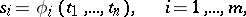 |
of the components of the tensor  with the following properties: Under a change of the set of numbers
with the following properties: Under a change of the set of numbers  defined by a non-singular linear transformation
defined by a non-singular linear transformation 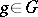 , the set of numbers
, the set of numbers 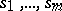 changes according to that of a covariant tensor
changes according to that of a covariant tensor  over
over  under the transformation
under the transformation 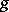 . In similar fashion one defines (by considering instead of one tensor
. In similar fashion one defines (by considering instead of one tensor 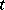 a finite collection of tensors) a joint covariant of the system of tensors. If instead, one replaces the covariance condition for the tensor
a finite collection of tensors) a joint covariant of the system of tensors. If instead, one replaces the covariance condition for the tensor  by contravariance, one obtains the notion of a contravariant.
by contravariance, one obtains the notion of a contravariant.
The notion of a covariant arose in the classical theory of invariants and is a special case of the notion of a comitant. The components of any tensor can be regarded as the coefficients of an appropriate form in several contravariant and covariant vectors (that is, vectors of 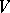 and its dual
and its dual 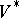 , cf. "form associated to a tensor" in the article Tensor on a vector space). Suppose that the form
, cf. "form associated to a tensor" in the article Tensor on a vector space). Suppose that the form 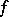 corresponds in this manner to the tensor
corresponds in this manner to the tensor 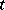 and that the form
and that the form 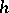 corresponds to its covariant
corresponds to its covariant  . Then
. Then 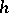 if a form of contravariant vectors only. In the classical theory of invariants
if a form of contravariant vectors only. In the classical theory of invariants 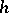 was called the covariant of
was called the covariant of 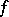 . A case that was particularly often considered is when
. A case that was particularly often considered is when 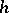 is a form in one single contravariant vector. The degree of this form is called the order of the covariant. If the coefficients of
is a form in one single contravariant vector. The degree of this form is called the order of the covariant. If the coefficients of  are polynomials in the coefficients of
are polynomials in the coefficients of  , then the highest of the degrees of these polynomials is called the degree of the covariant.
, then the highest of the degrees of these polynomials is called the degree of the covariant.
Example. Let  be a form of a degree
be a form of a degree  , where
, where  are the components of a contravariant vector. The form
are the components of a contravariant vector. The form 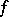 corresponds to a symmetric covariant tensor
corresponds to a symmetric covariant tensor 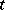 of valency
of valency  with components
with components 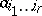 . Let
. Let
 |
Then the coefficients of 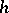 are the components of some covariant tensor
are the components of some covariant tensor  . The tensor
. The tensor  (or the form
(or the form  ) is a covariant of the tensor
) is a covariant of the tensor 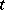 (or form
(or form  ). The form
). The form 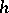 is called the Hessian of
is called the Hessian of  .
.
References
| [1] | G.B. Gurevich, "Foundations of the theory of algebraic invariants" , Noordhoff (1964) (Translated from Russian) |
Covariant. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Covariant&oldid=46542