Maximal compact subgroup
of a topological group 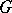
A compact subgroup (cf. Compact group) 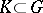 which is not contained as a proper subgroup in any compact subgroup of
which is not contained as a proper subgroup in any compact subgroup of 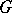 . For example,
. For example, 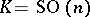 for
for 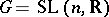 ,
, 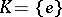 for a solvable simply-connected Lie group
for a solvable simply-connected Lie group 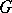 .
.
In an arbitrary group 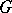 maximal compact subgroups need not exist (for example, if
maximal compact subgroups need not exist (for example, if 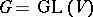 , where
, where 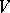 is an infinite-dimensional Hilbert space), and if they do exist there may be non-isomorphic ones among them.
is an infinite-dimensional Hilbert space), and if they do exist there may be non-isomorphic ones among them.
Maximal compact subgroups of Lie groups have been studied most. If 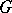 is a connected Lie group, then any compact subgroup of
is a connected Lie group, then any compact subgroup of 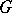 is contained in some maximal compact subgroup (in particular, maximal compact subgroups must exist) and all maximal compact subgroups of
is contained in some maximal compact subgroup (in particular, maximal compact subgroups must exist) and all maximal compact subgroups of 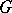 are connected and conjugate to each other. The space of the group
are connected and conjugate to each other. The space of the group 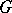 is diffeomorphic to
is diffeomorphic to 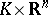 , therefore most of the topological questions about Lie groups reduce to the corresponding questions for compact Lie groups (cf. Lie group, compact).
, therefore most of the topological questions about Lie groups reduce to the corresponding questions for compact Lie groups (cf. Lie group, compact).
References
| [1] | E. Cartan, "La géometrie des groupes de transformations" J. Math. Pures Appl. , 6 (1927) pp. 1–119 |
| [2] | S. Helgason, "Differential geometry, Lie groups, and symmetric spaces" , Acad. Press (1978) |
Maximal compact subgroup. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Maximal_compact_subgroup&oldid=40957