Small category
A category 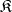 whose class of morphisms
whose class of morphisms  is a set. A small category
is a set. A small category 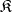 is called a
is called a 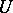 -category if
-category if 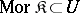 , where
, where 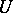 is a universe. For a small category
is a universe. For a small category  and an arbitrary locally small category
and an arbitrary locally small category 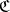 the category of covariant (contravariant) functors (cf. Functor) from
the category of covariant (contravariant) functors (cf. Functor) from 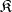 to
to 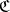 is locally small. In particular, the small categories form the closed category
is locally small. In particular, the small categories form the closed category 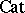 of small categories, one of the basic categories of mathematics [1].
of small categories, one of the basic categories of mathematics [1].
References
| [1] | F.W. Lawvere, "The category of categories as a foundation for mathematics" S. Eilenberg (ed.) et al. (ed.) , Proc. conf. categorical algebra (La Jolla, 1965) , Springer (1966) pp. 1–20 |
Comments
A category is called locally small if, for any pair of objects 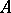 and
and 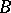 , the class of morphisms from
, the class of morphisms from 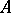 to
to 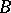 is a set. (Some authors assume this condition as part of the definition of a category.) A locally small category is small if and only if its class of objects is a set.
is a set. (Some authors assume this condition as part of the definition of a category.) A locally small category is small if and only if its class of objects is a set.
Cf. also Universe.
Small category. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Small_category&oldid=39511