Aliquot sequence
From Encyclopedia of Mathematics
starting from 
The sequence of natural numbers 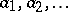 defined by the rule
defined by the rule
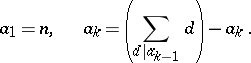 |
The sequence is said to be terminating if 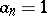 for some
for some  and eventually periodic if there is a
and eventually periodic if there is a  such that
such that 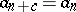 for
for  sufficiently large. If
sufficiently large. If 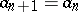 , then
, then 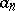 is a perfect number, while if
is a perfect number, while if 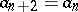 , then
, then 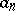 and
and 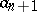 form an amicable pair (cf. also Amicable numbers).
form an amicable pair (cf. also Amicable numbers).
An example of an eventually periodic aliquot sequence is the sequence 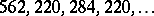 . Larger cycles are possible; e.g., a sequence with cycle length
. Larger cycles are possible; e.g., a sequence with cycle length 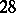 is known.
is known.
The Catalan–Dickson conjecture states that all aliquot sequences either terminate or are eventually periodic. This conjecture is still (1996) open, but generally thought to be false.
References
| [a1] | H.J.J. te Riele, "A theoretical and computational study of generalized aliquot sequences" , Math. Centre , Amsterdam (1976) |
How to Cite This Entry:
Aliquot sequence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Aliquot_sequence&oldid=33283
Aliquot sequence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Aliquot_sequence&oldid=33283
This article was adapted from an original article by M. Hazewinkel (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article