Difference between revisions of "Similarity region"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 48701 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
''similar region'' | ''similar region'' | ||
A generally used abbreviation of the term "critical region similar to a sample space" as used in mathematical statistics for a [[Critical region|critical region]] with non-randomized similarity of a statistical test. | A generally used abbreviation of the term "critical region similar to a sample space" as used in mathematical statistics for a [[Critical region|critical region]] with non-randomized similarity of a statistical test. | ||
| − | Let | + | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085170/s0851701.png" /> be a random variable taking values in a sample space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085170/s0851702.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085170/s0851703.png" />, and consider testing the compound hypothesis <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085170/s0851704.png" />: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085170/s0851705.png" /> against the alternative <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085170/s0851706.png" />: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085170/s0851707.png" />. Suppose that in order to test <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085170/s0851708.png" /> against <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085170/s0851709.png" />, a non-randomized [[Similar test|similar test]] of level <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085170/s08517010.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085170/s08517011.png" />) has been constructed, with critical function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085170/s08517012.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085170/s08517013.png" />. As this test is non-randomized, |
| − | be a random variable taking values in a sample space | ||
| − | |||
| − | and consider testing the compound hypothesis | ||
| − | |||
| − | against the alternative | ||
| − | |||
| − | Suppose that in order to test | ||
| − | against | ||
| − | a non-randomized [[Similar test|similar test]] of level | ||
| − | |||
| − | has been constructed, with critical function | ||
| − | |||
| − | As this test is non-randomized, | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085170/s08517014.png" /></td> <td valign="top" style="width:5%;text-align:right;">(1)</td></tr></table> | |
| − | |||
| − | |||
| − | where | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085170/s08517015.png" /> is a certain set in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085170/s08517016.png" />, called the critical set for the test (according to this test, the hypothesis <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085170/s08517017.png" /> is rejected in favour of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085170/s08517018.png" /> if the event <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085170/s08517019.png" /> is observed in an experiment). Also, the constructed test is a similar test, which means that |
| − | is a certain set in | ||
| − | called the critical set for the test (according to this test, the hypothesis | ||
| − | is rejected in favour of | ||
| − | if the event | ||
| − | is observed in an experiment). Also, the constructed test is a similar test, which means that | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085170/s08517020.png" /></td> <td valign="top" style="width:5%;text-align:right;">(2)</td></tr></table> | |
| − | |||
| − | |||
| − | |||
| − | It follows from (1) and (2) that the critical region | + | It follows from (1) and (2) that the critical region <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085170/s08517021.png" /> of a non-randomized similar test has the property: |
| − | of a non-randomized similar test has the property: | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085170/s08517022.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | Accordingly, J. Neyman and E.S. Pearson emphasized the latter feature of the critical set of a non-randomized similar test and called | + | Accordingly, J. Neyman and E.S. Pearson emphasized the latter feature of the critical set of a non-randomized similar test and called <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085170/s08517023.png" /> a "region similar to the sample space" <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085170/s08517024.png" />, in the sense that the two probabilities <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085170/s08517025.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085170/s08517026.png" /> are independent of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085170/s08517027.png" />. |
| − | a "region similar to the sample space" | ||
| − | in the sense that the two probabilities | ||
| − | and | ||
| − | are independent of | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> E.L. Lehmann, "Testing statistical hypotheses" , Wiley (1986)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> B.L. van der Waerden, "Mathematische Statistik" , Springer (1957)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> J. Neyman, E.S. Pearson, "On the problem of the most efficient tests of statistical hypotheses" ''Philos. Trans. Roy. Soc. London Ser. A'' , '''231''' (1933) pp. 289–337</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> E.L. Lehmann, H. Scheffé, "Completeness, similar regions, and unbiased estimation I" ''Sankhyā'' , '''10''' (1950) pp. 305–340</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> E.L. Lehmann, H. Scheffé, "Completeness, similar regions, and unbiased estimation II" ''Sankhyā'' , '''15''' (1955) pp. 219–236</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> E.L. Lehmann, "Testing statistical hypotheses" , Wiley (1986)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> B.L. van der Waerden, "Mathematische Statistik" , Springer (1957)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> J. Neyman, E.S. Pearson, "On the problem of the most efficient tests of statistical hypotheses" ''Philos. Trans. Roy. Soc. London Ser. A'' , '''231''' (1933) pp. 289–337</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> E.L. Lehmann, H. Scheffé, "Completeness, similar regions, and unbiased estimation I" ''Sankhyā'' , '''10''' (1950) pp. 305–340</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> E.L. Lehmann, H. Scheffé, "Completeness, similar regions, and unbiased estimation II" ''Sankhyā'' , '''15''' (1955) pp. 219–236</TD></TR></table> | ||
Revision as of 14:53, 7 June 2020
similar region
A generally used abbreviation of the term "critical region similar to a sample space" as used in mathematical statistics for a critical region with non-randomized similarity of a statistical test.
Let 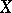 be a random variable taking values in a sample space
be a random variable taking values in a sample space 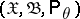 ,
, 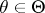 , and consider testing the compound hypothesis
, and consider testing the compound hypothesis 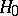 :
:  against the alternative
against the alternative 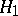 :
: 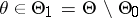 . Suppose that in order to test
. Suppose that in order to test 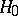 against
against 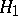 , a non-randomized similar test of level
, a non-randomized similar test of level 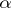 (
(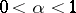 ) has been constructed, with critical function
) has been constructed, with critical function 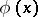 ,
, 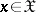 . As this test is non-randomized,
. As this test is non-randomized,
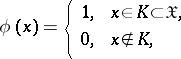 | (1) |
where 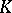 is a certain set in
is a certain set in 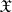 , called the critical set for the test (according to this test, the hypothesis
, called the critical set for the test (according to this test, the hypothesis 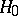 is rejected in favour of
is rejected in favour of 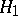 if the event
if the event 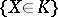 is observed in an experiment). Also, the constructed test is a similar test, which means that
is observed in an experiment). Also, the constructed test is a similar test, which means that
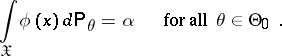 | (2) |
It follows from (1) and (2) that the critical region 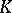 of a non-randomized similar test has the property:
of a non-randomized similar test has the property:
 |
Accordingly, J. Neyman and E.S. Pearson emphasized the latter feature of the critical set of a non-randomized similar test and called 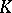 a "region similar to the sample space"
a "region similar to the sample space" 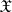 , in the sense that the two probabilities
, in the sense that the two probabilities 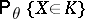 and
and 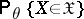 are independent of
are independent of  .
.
References
| [1] | E.L. Lehmann, "Testing statistical hypotheses" , Wiley (1986) |
| [2] | B.L. van der Waerden, "Mathematische Statistik" , Springer (1957) |
| [3] | J. Neyman, E.S. Pearson, "On the problem of the most efficient tests of statistical hypotheses" Philos. Trans. Roy. Soc. London Ser. A , 231 (1933) pp. 289–337 |
| [4] | E.L. Lehmann, H. Scheffé, "Completeness, similar regions, and unbiased estimation I" Sankhyā , 10 (1950) pp. 305–340 |
| [5] | E.L. Lehmann, H. Scheffé, "Completeness, similar regions, and unbiased estimation II" Sankhyā , 15 (1955) pp. 219–236 |
Similarity region. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Similarity_region&oldid=49424