Difference between revisions of "Lefschetz formula"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | l0579801.png | ||
| + | $#A+1 = 111 n = 2 | ||
| + | $#C+1 = 111 : ~/encyclopedia/old_files/data/L057/L.0507980 Lefschetz formula | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
A formula that expresses the number of fixed points of an endomorphism of a topological space in terms of the traces of the corresponding endomorphisms in the cohomology groups. | A formula that expresses the number of fixed points of an endomorphism of a topological space in terms of the traces of the corresponding endomorphisms in the cohomology groups. | ||
| − | This formula was first established by S. Lefschetz for finite-dimensional orientable topological manifolds [[#References|[1]]] and for finite cell complexes (see [[#References|[2]]], [[#References|[3]]]). These papers of Lefschetz were preceded by a paper of L.E.J. Brouwer (1911) on the fixed point of a continuous mapping of an | + | This formula was first established by S. Lefschetz for finite-dimensional orientable topological manifolds [[#References|[1]]] and for finite cell complexes (see [[#References|[2]]], [[#References|[3]]]). These papers of Lefschetz were preceded by a paper of L.E.J. Brouwer (1911) on the fixed point of a continuous mapping of an $ n $- |
| + | dimensional sphere into itself. A new version of the proof of the Lefschetz formula for finite cell complexes was given by H. Hopf (see [[#References|[9]]]). | ||
| − | Let | + | Let $ X $ |
| + | be a connected orientable $ n $- | ||
| + | dimensional compact topological [[Manifold|manifold]] or an $ n $- | ||
| + | dimensional finite [[Cell complex|cell complex]], let $ f : X \rightarrow X $ | ||
| + | be a [[Continuous mapping|continuous mapping]] and let $ \Lambda ( f , X ) $ | ||
| + | be the [[Lefschetz number|Lefschetz number]] of $ f $. | ||
| + | Assume that all fixed points of the mapping $ f : X \rightarrow X $ | ||
| + | are isolated. For each fixed point $ x \in X $, | ||
| + | let $ i ( x) $ | ||
| + | be its Kronecker index (the local degree (cf. [[Degree of a mapping|Degree of a mapping]]) of $ f $ | ||
| + | in a neighbourhood of $ x $). | ||
| + | Then the Lefschetz formula for $ X $ | ||
| + | and $ f $ | ||
| + | has the form | ||
| − | + | $$ \tag{1 } | |
| + | \sum _ {f ( x) = x } i ( x) = \Lambda ( f , X ) . | ||
| + | $$ | ||
There is, [[#References|[8]]], a generalization of the Lefschetz formula to the case of arbitrary continuous mappings of compact Euclidean neighbourhood retracts. | There is, [[#References|[8]]], a generalization of the Lefschetz formula to the case of arbitrary continuous mappings of compact Euclidean neighbourhood retracts. | ||
| − | Let | + | Let $ X $ |
| + | be a differentiable compact orientable manifold and let $ f : X \rightarrow X $ | ||
| + | be a differentiable mapping. A fixed point $ x \in X $ | ||
| + | for $ f $ | ||
| + | is said to be non-singular if it is isolated and if $ \mathop{\rm det} ( df _ {x} - E ) \neq 0 $, | ||
| + | where $ df _ {x} : T _ {x} ( X) \rightarrow T _ {x} ( X) $ | ||
| + | is the differential of $ f $ | ||
| + | at $ x $ | ||
| + | and $ E $ | ||
| + | is the identity transformation. For a non-singular point $ x \in X $ | ||
| + | its index $ i ( x) $ | ||
| + | coincides with the number $ \mathop{\rm sgn} \mathop{\rm det} ( df _ {x} - E ) $. | ||
| + | In this case the Lefschetz formula (1) shows that the Lefschetz number $ \Lambda ( f , X ) $ | ||
| + | is equal to the difference between the number of fixed points with index $ + 1 $ | ||
| + | and the number of fixed points with index $ - 1 $; | ||
| + | in particular, it does not exceed the total number of fixed points. In this case the left-hand side of (1) can be determined in the same way as the intersection index $ \Gamma _ {f} \Delta $ | ||
| + | on $ X \times X $, | ||
| + | where $ \Gamma _ {f} $ | ||
| + | is the graph of $ f $ | ||
| + | and $ \Delta \subset X \times X $ | ||
| + | is the diagonal (cf. [[Intersection index (in algebraic geometry)|Intersection index (in algebraic geometry)]]). | ||
| − | A consequence of the Lefschetz formula is the Hopf formula, which asserts that the [[Euler characteristic|Euler characteristic]] | + | A consequence of the Lefschetz formula is the Hopf formula, which asserts that the [[Euler characteristic|Euler characteristic]] $ \chi ( X) $ |
| + | is equal to the sum of the indices of the zeros of a global $ C ^ \infty $- | ||
| + | vector field $ v $ | ||
| + | on $ X $( | ||
| + | it is assumed that all zeros of $ v $ | ||
| + | are isolated) (see [[#References|[5]]]). | ||
| − | There is a version of the Lefschetz formula for compact complex manifolds and the Dolbeault cohomology (see [[#References|[5]]]). Let | + | There is a version of the Lefschetz formula for compact complex manifolds and the Dolbeault cohomology (see [[#References|[5]]]). Let $ X $ |
| + | be a compact complex manifold of dimension $ m $ | ||
| + | and let $ f : X \rightarrow X $ | ||
| + | a be holomorphic mapping with non-singular fixed points. Let $ H ^ {p,q} ( X) $ | ||
| + | be the Dolbeault cohomology of $ X $ | ||
| + | of type $ ( p , q ) $( | ||
| + | cf. [[Differential form|Differential form]]) and let $ f ^ { * } : H ^ {p,q} ( X) \rightarrow H ^ {p,q} ( X) $ | ||
| + | be the endomorphism induced by $ f $. | ||
| + | The number | ||
| − | + | $$ | |
| + | \Lambda ( f , {\mathcal O} _ {X} ) = \sum _ { q= } 0 ^ { m } (- 1) ^ {q} \mathop{\rm Tr} ( | ||
| + | f ^ { * } ; H ^ {0,q} ( X) ) | ||
| + | $$ | ||
is called the holomorphic Lefschetz number. One then has the following holomorphic Lefschetz formula: | is called the holomorphic Lefschetz number. One then has the following holomorphic Lefschetz formula: | ||
| − | + | $$ | |
| + | \Lambda ( f , {\mathcal O} _ {X} ) = \sum _ {f ( x) = x } | ||
| + | \frac{1}{ | ||
| + | \mathop{\rm det} ( E - df _ {x} ) } | ||
| + | , | ||
| + | $$ | ||
| − | where | + | where $ df _ {x} $ |
| + | is the holomorphic differential of $ f $ | ||
| + | at $ x $. | ||
| − | In abstract algebraic geometry the Lefschetz formula has served as a starting point in the search for [[Weil cohomology|Weil cohomology]] in connection with Weil's conjectures about zeta-functions of algebraic varieties defined over finite fields (cf. [[Zeta-function|Zeta-function]]). An analogue of the Lefschetz formula in abstract algebraic geometry has been established for | + | In abstract algebraic geometry the Lefschetz formula has served as a starting point in the search for [[Weil cohomology|Weil cohomology]] in connection with Weil's conjectures about zeta-functions of algebraic varieties defined over finite fields (cf. [[Zeta-function|Zeta-function]]). An analogue of the Lefschetz formula in abstract algebraic geometry has been established for $ l $- |
| + | adic cohomology with compact support and with coefficients in constructible $ \mathbf Q _ {l} $- | ||
| + | sheaves, where $ \mathbf Q _ {l} $ | ||
| + | is the field of $ l $- | ||
| + | adic numbers and where $ l $ | ||
| + | is a prime number distinct from the characteristic of the field $ k $. | ||
| + | This formula is often called the trace formula. | ||
| − | Let | + | Let $ X $ |
| + | be an [[Algebraic variety|algebraic variety]] (or [[Scheme|scheme]]) over a finite field $ k $, | ||
| + | let $ F : X \rightarrow X $ | ||
| + | be a Frobenius morphism (cf. e.g. [[Frobenius automorphism|Frobenius automorphism]]), $ {\mathcal F} $ | ||
| + | a sheaf on $ X $, | ||
| + | and let $ H _ {c} ^ {i} ( X , {\mathcal F} ) $ | ||
| + | be cohomology with compact support of the variety (scheme) $ X $ | ||
| + | with coefficients in $ {\mathcal F} $. | ||
| + | Then the morphism $ F $ | ||
| + | determines a cohomology endomorphism | ||
| − | + | $$ | |
| + | F ^ { * } : H _ {c} ^ {i} ( X , {\mathcal F} ) \rightarrow H _ {c} ^ {i} ( X ,\ | ||
| + | {\mathcal F} ) . | ||
| + | $$ | ||
| − | If | + | If $ k _ {n} \supset k $ |
| + | is an extension of $ k $ | ||
| + | of degree $ n $ | ||
| + | and if $ X _ {n} = X \otimes k _ {n} $, | ||
| + | $ {\mathcal F} _ {n} = {\mathcal F} \otimes k _ {n} $ | ||
| + | are the variety (scheme) and sheaf obtained from $ X $ | ||
| + | and $ {\mathcal F} $ | ||
| + | by extending the field of scalars, then the corresponding Frobenius morphism $ F _ {n} : X _ {n} \rightarrow X _ {n} $ | ||
| + | coincides with the $ n $- | ||
| + | th power $ F ^ { n } $ | ||
| + | of $ F $. | ||
| − | Now let | + | Now let $ X $ |
| + | be a separable scheme of finite type over the finite field $ k $ | ||
| + | of $ q $ | ||
| + | elements, let $ {\mathcal F} $ | ||
| + | be a constructible $ \mathbf Q _ {l} $- | ||
| + | sheaf on $ X $, | ||
| + | $ l $ | ||
| + | a prime number distinct from the characteristic of $ k $, | ||
| + | and $ X ^ {F ^ {n} } $ | ||
| + | the set of fixed geometric points of the morphism $ F ^ { n } $ | ||
| + | or, equivalently, the set $ X ( k _ {n} ) $ | ||
| + | of geometric points of the scheme $ X $ | ||
| + | with values in the field $ k _ {n} $. | ||
| + | Then for any integer $ n \geq 1 $ | ||
| + | the following Lefschetz formula (or trace formula) holds (see [[#References|[6]]], [[#References|[7]]]): | ||
| − | + | $$ \tag{2 } | |
| + | \sum _ {x \in X ^ {F ^ {n} } } \mathop{\rm Tr} ( F ^ { n* } , {\mathcal F} _ {x} ) = \ | ||
| + | \sum _ { i } (- 1) ^ {i} \mathop{\rm Tr} ( F ^ { * n } , H _ {c} ^ {i} ( X ,\ | ||
| + | {\mathcal F} )) , | ||
| + | $$ | ||
| − | where | + | where $ {\mathcal F} _ {x} $ |
| + | is the stalk of $ {\mathcal F} $ | ||
| + | over $ x $. | ||
| + | In the case of the constant sheaf $ {\mathcal F} = \mathbf Q _ {l} $ | ||
| + | one has $ \mathop{\rm Tr} ( F ^ { n* } , \mathbf Q _ {l} ) = 1 $ | ||
| + | and the left-hand side of (2) is none other than the number of geometric points of $ X $ | ||
| + | with values in $ k _ {n} $. | ||
| + | In particular, for $ n= 1 $ | ||
| + | this is simply the number of points of $ X $ | ||
| + | with values in the ground field $ k $. | ||
| + | If $ X $ | ||
| + | is proper over $ k $( | ||
| + | for example, if $ X $ | ||
| + | is a complete algebraic variety over $ k $), | ||
| + | then $ H _ {c} ^ {i} ( X , {\mathcal F} ) = H ^ {i} ( X , {\mathcal F} ) $ | ||
| + | and the right-hand side of (2) is an alternating sum of the traces of the Frobenius endomorphism in the ordinary cohomology of $ X $. | ||
There are (see [[#References|[7]]]) generalizations of formula (2). | There are (see [[#References|[7]]]) generalizations of formula (2). | ||
| Line 41: | Line 173: | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> S. Lefschetz, "Intersections and transformations of complexes and manifolds" ''Trans. Amer. Soc.'' , '''28''' (1926) pp. 1–49 {{MR|1501331}} {{ZBL|52.0572.02}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> S. Lefschetz, "The residual set of a complex manifold and related questions" ''Proc. Nat. Acad. Sci. USA'' , '''13''' (1927) pp. 614–622 {{MR|}} {{ZBL|53.0553.01}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> S. Lefschetz, "On the fixed point formula" ''Ann. of Math. (2)'' , '''38''' (1937) pp. 819–822 {{MR|1503373}} {{ZBL|0018.17703}} {{ZBL|63.0563.02}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> S.L. Kleiman, "Algebraic cycles and the Weil conjectures" A. Grothendieck (ed.) J. Giraud (ed.) et al. (ed.) , ''Dix exposés sur la cohomologie des schémas'' , North-Holland & Masson (1968) pp. 359–386 {{MR|0292838}} {{ZBL|0198.25902}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> P.A. Griffiths, J.E. Harris, "Principles of algebraic geometry" , Wiley (Interscience) (1978) {{MR|0507725}} {{ZBL|0408.14001}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> P. Deligne, "Cohomologie étale (SGA 4 1/2)" , ''Lect. notes in math.'' , '''569''' , Springer (1977)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> A. Grothendieck, I. Bucur, C. Honzel, L. Illusie, J.-P. Jouanolou, J.-P. Serre, "Cohomologie <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057980/l057980112.png" />-adique et fonctions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057980/l057980113.png" />. SGA 5" , ''Lect. notes in math.'' , '''589''' , Springer (1977) {{MR|491704}} {{ZBL|}} </TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> A. Dold, "Lectures on algebraic topology" , Springer (1980) {{MR|0606196}} {{ZBL|0434.55001}} </TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> H. Seifert, W. Threlfall, "A textbook of topology" , Acad. Press (1980) (Translated from German) {{MR|0575168}} {{ZBL|0469.55001}} </TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> S. Lefschetz, "Intersections and transformations of complexes and manifolds" ''Trans. Amer. Soc.'' , '''28''' (1926) pp. 1–49 {{MR|1501331}} {{ZBL|52.0572.02}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> S. Lefschetz, "The residual set of a complex manifold and related questions" ''Proc. Nat. Acad. Sci. USA'' , '''13''' (1927) pp. 614–622 {{MR|}} {{ZBL|53.0553.01}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> S. Lefschetz, "On the fixed point formula" ''Ann. of Math. (2)'' , '''38''' (1937) pp. 819–822 {{MR|1503373}} {{ZBL|0018.17703}} {{ZBL|63.0563.02}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> S.L. Kleiman, "Algebraic cycles and the Weil conjectures" A. Grothendieck (ed.) J. Giraud (ed.) et al. (ed.) , ''Dix exposés sur la cohomologie des schémas'' , North-Holland & Masson (1968) pp. 359–386 {{MR|0292838}} {{ZBL|0198.25902}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> P.A. Griffiths, J.E. Harris, "Principles of algebraic geometry" , Wiley (Interscience) (1978) {{MR|0507725}} {{ZBL|0408.14001}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> P. Deligne, "Cohomologie étale (SGA 4 1/2)" , ''Lect. notes in math.'' , '''569''' , Springer (1977)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> A. Grothendieck, I. Bucur, C. Honzel, L. Illusie, J.-P. Jouanolou, J.-P. Serre, "Cohomologie <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057980/l057980112.png" />-adique et fonctions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057980/l057980113.png" />. SGA 5" , ''Lect. notes in math.'' , '''589''' , Springer (1977) {{MR|491704}} {{ZBL|}} </TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> A. Dold, "Lectures on algebraic topology" , Springer (1980) {{MR|0606196}} {{ZBL|0434.55001}} </TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> H. Seifert, W. Threlfall, "A textbook of topology" , Acad. Press (1980) (Translated from German) {{MR|0575168}} {{ZBL|0469.55001}} </TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
Revision as of 22:16, 5 June 2020
A formula that expresses the number of fixed points of an endomorphism of a topological space in terms of the traces of the corresponding endomorphisms in the cohomology groups.
This formula was first established by S. Lefschetz for finite-dimensional orientable topological manifolds [1] and for finite cell complexes (see [2], [3]). These papers of Lefschetz were preceded by a paper of L.E.J. Brouwer (1911) on the fixed point of a continuous mapping of an $ n $- dimensional sphere into itself. A new version of the proof of the Lefschetz formula for finite cell complexes was given by H. Hopf (see [9]).
Let $ X $ be a connected orientable $ n $- dimensional compact topological manifold or an $ n $- dimensional finite cell complex, let $ f : X \rightarrow X $ be a continuous mapping and let $ \Lambda ( f , X ) $ be the Lefschetz number of $ f $. Assume that all fixed points of the mapping $ f : X \rightarrow X $ are isolated. For each fixed point $ x \in X $, let $ i ( x) $ be its Kronecker index (the local degree (cf. Degree of a mapping) of $ f $ in a neighbourhood of $ x $). Then the Lefschetz formula for $ X $ and $ f $ has the form
$$ \tag{1 } \sum _ {f ( x) = x } i ( x) = \Lambda ( f , X ) . $$
There is, [8], a generalization of the Lefschetz formula to the case of arbitrary continuous mappings of compact Euclidean neighbourhood retracts.
Let $ X $ be a differentiable compact orientable manifold and let $ f : X \rightarrow X $ be a differentiable mapping. A fixed point $ x \in X $ for $ f $ is said to be non-singular if it is isolated and if $ \mathop{\rm det} ( df _ {x} - E ) \neq 0 $, where $ df _ {x} : T _ {x} ( X) \rightarrow T _ {x} ( X) $ is the differential of $ f $ at $ x $ and $ E $ is the identity transformation. For a non-singular point $ x \in X $ its index $ i ( x) $ coincides with the number $ \mathop{\rm sgn} \mathop{\rm det} ( df _ {x} - E ) $. In this case the Lefschetz formula (1) shows that the Lefschetz number $ \Lambda ( f , X ) $ is equal to the difference between the number of fixed points with index $ + 1 $ and the number of fixed points with index $ - 1 $; in particular, it does not exceed the total number of fixed points. In this case the left-hand side of (1) can be determined in the same way as the intersection index $ \Gamma _ {f} \Delta $ on $ X \times X $, where $ \Gamma _ {f} $ is the graph of $ f $ and $ \Delta \subset X \times X $ is the diagonal (cf. Intersection index (in algebraic geometry)).
A consequence of the Lefschetz formula is the Hopf formula, which asserts that the Euler characteristic $ \chi ( X) $ is equal to the sum of the indices of the zeros of a global $ C ^ \infty $- vector field $ v $ on $ X $( it is assumed that all zeros of $ v $ are isolated) (see [5]).
There is a version of the Lefschetz formula for compact complex manifolds and the Dolbeault cohomology (see [5]). Let $ X $ be a compact complex manifold of dimension $ m $ and let $ f : X \rightarrow X $ a be holomorphic mapping with non-singular fixed points. Let $ H ^ {p,q} ( X) $ be the Dolbeault cohomology of $ X $ of type $ ( p , q ) $( cf. Differential form) and let $ f ^ { * } : H ^ {p,q} ( X) \rightarrow H ^ {p,q} ( X) $ be the endomorphism induced by $ f $. The number
$$ \Lambda ( f , {\mathcal O} _ {X} ) = \sum _ { q= } 0 ^ { m } (- 1) ^ {q} \mathop{\rm Tr} ( f ^ { * } ; H ^ {0,q} ( X) ) $$
is called the holomorphic Lefschetz number. One then has the following holomorphic Lefschetz formula:
$$ \Lambda ( f , {\mathcal O} _ {X} ) = \sum _ {f ( x) = x } \frac{1}{ \mathop{\rm det} ( E - df _ {x} ) } , $$
where $ df _ {x} $ is the holomorphic differential of $ f $ at $ x $.
In abstract algebraic geometry the Lefschetz formula has served as a starting point in the search for Weil cohomology in connection with Weil's conjectures about zeta-functions of algebraic varieties defined over finite fields (cf. Zeta-function). An analogue of the Lefschetz formula in abstract algebraic geometry has been established for $ l $- adic cohomology with compact support and with coefficients in constructible $ \mathbf Q _ {l} $- sheaves, where $ \mathbf Q _ {l} $ is the field of $ l $- adic numbers and where $ l $ is a prime number distinct from the characteristic of the field $ k $. This formula is often called the trace formula.
Let $ X $ be an algebraic variety (or scheme) over a finite field $ k $, let $ F : X \rightarrow X $ be a Frobenius morphism (cf. e.g. Frobenius automorphism), $ {\mathcal F} $ a sheaf on $ X $, and let $ H _ {c} ^ {i} ( X , {\mathcal F} ) $ be cohomology with compact support of the variety (scheme) $ X $ with coefficients in $ {\mathcal F} $. Then the morphism $ F $ determines a cohomology endomorphism
$$ F ^ { * } : H _ {c} ^ {i} ( X , {\mathcal F} ) \rightarrow H _ {c} ^ {i} ( X ,\ {\mathcal F} ) . $$
If $ k _ {n} \supset k $ is an extension of $ k $ of degree $ n $ and if $ X _ {n} = X \otimes k _ {n} $, $ {\mathcal F} _ {n} = {\mathcal F} \otimes k _ {n} $ are the variety (scheme) and sheaf obtained from $ X $ and $ {\mathcal F} $ by extending the field of scalars, then the corresponding Frobenius morphism $ F _ {n} : X _ {n} \rightarrow X _ {n} $ coincides with the $ n $- th power $ F ^ { n } $ of $ F $.
Now let $ X $ be a separable scheme of finite type over the finite field $ k $ of $ q $ elements, let $ {\mathcal F} $ be a constructible $ \mathbf Q _ {l} $- sheaf on $ X $, $ l $ a prime number distinct from the characteristic of $ k $, and $ X ^ {F ^ {n} } $ the set of fixed geometric points of the morphism $ F ^ { n } $ or, equivalently, the set $ X ( k _ {n} ) $ of geometric points of the scheme $ X $ with values in the field $ k _ {n} $. Then for any integer $ n \geq 1 $ the following Lefschetz formula (or trace formula) holds (see [6], [7]):
$$ \tag{2 } \sum _ {x \in X ^ {F ^ {n} } } \mathop{\rm Tr} ( F ^ { n* } , {\mathcal F} _ {x} ) = \ \sum _ { i } (- 1) ^ {i} \mathop{\rm Tr} ( F ^ { * n } , H _ {c} ^ {i} ( X ,\ {\mathcal F} )) , $$
where $ {\mathcal F} _ {x} $ is the stalk of $ {\mathcal F} $ over $ x $. In the case of the constant sheaf $ {\mathcal F} = \mathbf Q _ {l} $ one has $ \mathop{\rm Tr} ( F ^ { n* } , \mathbf Q _ {l} ) = 1 $ and the left-hand side of (2) is none other than the number of geometric points of $ X $ with values in $ k _ {n} $. In particular, for $ n= 1 $ this is simply the number of points of $ X $ with values in the ground field $ k $. If $ X $ is proper over $ k $( for example, if $ X $ is a complete algebraic variety over $ k $), then $ H _ {c} ^ {i} ( X , {\mathcal F} ) = H ^ {i} ( X , {\mathcal F} ) $ and the right-hand side of (2) is an alternating sum of the traces of the Frobenius endomorphism in the ordinary cohomology of $ X $.
There are (see [7]) generalizations of formula (2).
References
| [1] | S. Lefschetz, "Intersections and transformations of complexes and manifolds" Trans. Amer. Soc. , 28 (1926) pp. 1–49 MR1501331 Zbl 52.0572.02 |
| [2] | S. Lefschetz, "The residual set of a complex manifold and related questions" Proc. Nat. Acad. Sci. USA , 13 (1927) pp. 614–622 Zbl 53.0553.01 |
| [3] | S. Lefschetz, "On the fixed point formula" Ann. of Math. (2) , 38 (1937) pp. 819–822 MR1503373 Zbl 0018.17703 Zbl 63.0563.02 |
| [4] | S.L. Kleiman, "Algebraic cycles and the Weil conjectures" A. Grothendieck (ed.) J. Giraud (ed.) et al. (ed.) , Dix exposés sur la cohomologie des schémas , North-Holland & Masson (1968) pp. 359–386 MR0292838 Zbl 0198.25902 |
| [5] | P.A. Griffiths, J.E. Harris, "Principles of algebraic geometry" , Wiley (Interscience) (1978) MR0507725 Zbl 0408.14001 |
| [6] | P. Deligne, "Cohomologie étale (SGA 4 1/2)" , Lect. notes in math. , 569 , Springer (1977) |
| [7] | A. Grothendieck, I. Bucur, C. Honzel, L. Illusie, J.-P. Jouanolou, J.-P. Serre, "Cohomologie 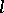 -adique et fonctions -adique et fonctions 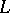 . SGA 5" , Lect. notes in math. , 589 , Springer (1977) MR491704 . SGA 5" , Lect. notes in math. , 589 , Springer (1977) MR491704 |
| [8] | A. Dold, "Lectures on algebraic topology" , Springer (1980) MR0606196 Zbl 0434.55001 |
| [9] | H. Seifert, W. Threlfall, "A textbook of topology" , Acad. Press (1980) (Translated from German) MR0575168 Zbl 0469.55001 |
Comments
For the Lefschetz formula in abstract algebraic geometry and its generalizations by A. Grothendieck see also [a1].
References
| [a1] | E. Feitag, R. Kiehl, "Etale cohomology and the Weil conjecture" , Springer (1988) MR926276 |
Lefschetz formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lefschetz_formula&oldid=47604