Difference between revisions of "Whitehead group"
(Importing text file) |
m (link) |
||
| Line 7: | Line 7: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097770/w0977707.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097770/w0977707.png" /></td> </tr></table> | ||
| − | let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097770/w0977708.png" />. A matrix differing from the | + | let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097770/w0977708.png" />. A matrix differing from the identity matrix in a single non-diagonal entry is called an [[elementary matrix]]. The subgroup <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097770/w0977709.png" /> generated by all elementary matrices coincides with the commutator group of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097770/w09777010.png" />. The commutator quotient group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097770/w09777011.png" /> is called the Whitehead group of the ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097770/w09777012.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097770/w09777013.png" /> be the element corresponding to the matrix |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097770/w09777014.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097770/w09777014.png" /></td> </tr></table> | ||
Revision as of 22:15, 10 January 2015
An Abelian group associated with an associative ring in the following manner. It was introduced by J.H.C. Whitehead [1]. Let 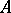 be an associative ring with unit element and let
be an associative ring with unit element and let 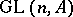 be the group of invertible
be the group of invertible  -matrices over
-matrices over  . There are natural imbeddings
. There are natural imbeddings
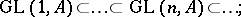 |
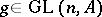 goes to
goes to
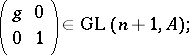 |
let  . A matrix differing from the identity matrix in a single non-diagonal entry is called an elementary matrix. The subgroup
. A matrix differing from the identity matrix in a single non-diagonal entry is called an elementary matrix. The subgroup 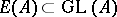 generated by all elementary matrices coincides with the commutator group of
generated by all elementary matrices coincides with the commutator group of 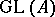 . The commutator quotient group
. The commutator quotient group 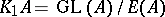 is called the Whitehead group of the ring
is called the Whitehead group of the ring 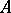 . Let
. Let  be the element corresponding to the matrix
be the element corresponding to the matrix
 |
It has order 2. The quotient group 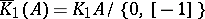 is called the reduced Whitehead group of the ring
is called the reduced Whitehead group of the ring 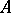 .
.
Let 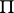 be a multiplicative group and let
be a multiplicative group and let 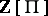 be its group ring over
be its group ring over 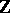 . There is a natural homomorphism
. There is a natural homomorphism 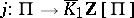 coming from the inclusion of
coming from the inclusion of 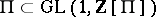 . The quotient group
. The quotient group  is called the Whitehead group of the group
is called the Whitehead group of the group  .
.
Given a homomorphism of groups  , there is a natural induced homomorphism
, there is a natural induced homomorphism  , such that
, such that 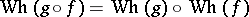 for
for 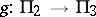 . Thus
. Thus 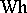 is a covariant functor from the category of groups into the category of Abelian groups. If
is a covariant functor from the category of groups into the category of Abelian groups. If 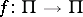 is an inner automorphism, then
is an inner automorphism, then  .
.
The Whitehead group of the fundamental group of a space is independent of the choice of a base point and is essential for the definition of an important invariant of mappings, the Whitehead torsion.
References
| [1] | J.H.C. Whitehead, "Simple homotopy types" Amer. J. Math. , 72 (1950) pp. 1–57 |
| [2] | J.W. Milnor, "Whitehead torsion" Bull. Amer. Math. Soc. , 72 (1966) pp. 358–426 |
| [3] | J.W. Milnor, "Introduction to algebraic  -theory" , Princeton Univ. Press (1971) -theory" , Princeton Univ. Press (1971) |
Comments
If 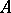 is commutative, the determinant and, hence, the special linear groups
is commutative, the determinant and, hence, the special linear groups 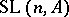 are defined. Using these instead of the
are defined. Using these instead of the 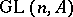 one obtains the special Whitehead group
one obtains the special Whitehead group 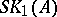 . One has
. One has  where
where 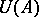 is the group of units of
is the group of units of 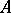 .
.
Whitehead group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Whitehead_group&oldid=36233