Difference between revisions of "Density of a probability distribution"
(Importing text file) |
(→References: Feller: internal link) |
||
| Line 62: | Line 62: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> Yu.V. [Yu.V. Prokhorov] Prohorov, Yu.A. Rozanov, "Probability theory, basic concepts. Limit theorems, random processes", Springer (1969) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> W. Feller, [[Feller, "An introduction to probability theory and its applications"|"An introduction to probability theory and its applications"]], '''2''', Wiley (1971)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> E.L. Lehmann, "Testing statistical hypotheses", Wiley (1986)</TD></TR></table> |
Revision as of 09:19, 4 May 2012
probability density
The derivative of the distribution function corresponding to an absolutely-continuous probability measure.
Let 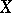 be a random vector taking values in an
be a random vector taking values in an  -dimensional Euclidean space
-dimensional Euclidean space 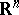
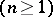 , let
, let 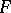 be its distribution function, and let there exist a non-negative function
be its distribution function, and let there exist a non-negative function 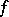 such that
such that
 |
for any real  . Then
. Then 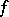 is called the probability density of
is called the probability density of 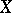 , and for any Borel set
, and for any Borel set 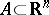 ,
,
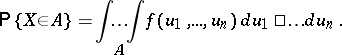 |
Any non-negative integrable function 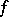 satisfy the condition
satisfy the condition
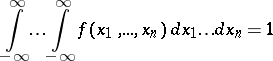 |
is the probability density of some random vector.
If two random vectors 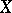 and
and 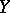 taking values in
taking values in 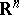 are independent and have probability densities
are independent and have probability densities 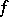 and
and 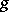 respectively, then the random vector
respectively, then the random vector 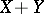 has the probability density
has the probability density 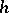 that is the convolution of
that is the convolution of 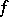 and
and 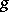 :
:
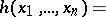 |
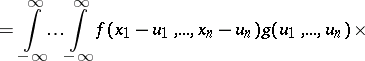 |
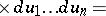 |
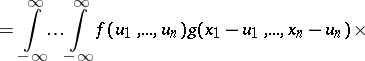 |
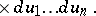 |
Let 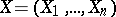 and
and 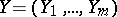 be random vectors taking values in
be random vectors taking values in 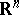 and
and 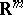
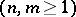 and having probability densities
and having probability densities 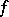 and
and 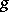 respectively, and let
respectively, and let 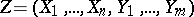 be a random vector in
be a random vector in 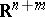 . If then
. If then 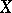 and
and 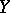 are independent,
are independent, 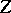 has the probability density
has the probability density 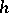 , which is called the joint probability density of the random vectors
, which is called the joint probability density of the random vectors 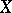 and
and  , where
, where
 | (1) |
Conversely, if 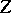 has a probability density that satisfies (1), then
has a probability density that satisfies (1), then 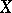 and
and  are independent.
are independent.
The characteristic function 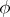 of a random vector
of a random vector 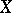 having a probability density
having a probability density 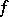 is expressed by
is expressed by
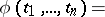 |
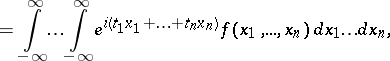 |
where if 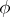 is absolutely integrable then
is absolutely integrable then 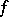 is a bounded continuous function, and
is a bounded continuous function, and
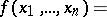 |
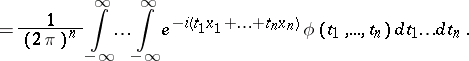 |
The probability density 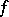 and the corresponding characteristic function
and the corresponding characteristic function 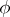 are related also by the following relation (Plancherel's identity): The function
are related also by the following relation (Plancherel's identity): The function 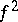 is integrable if and only if the function
is integrable if and only if the function 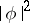 is integrable, and in that case
is integrable, and in that case
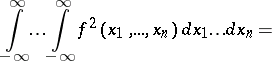 |
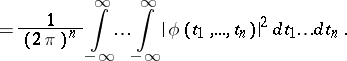 |
Let 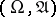 be a measurable space, and let
be a measurable space, and let  and
and 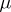 be
be 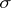 -finite measures on
-finite measures on 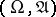 with
with  absolutely continuous with respect to
absolutely continuous with respect to 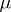 , i.e.
, i.e. 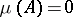 implies
implies 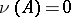 ,
, 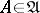 . In that case there exists on
. In that case there exists on 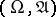 a non-negative measurable function
a non-negative measurable function 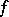 such that
such that
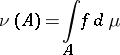 |
for any 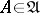 . The function
. The function 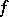 is called the Radon–Nikodým derivative of
is called the Radon–Nikodým derivative of  with respect to
with respect to 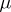 , while if
, while if  is a probability measure, it is also the probability density of
is a probability measure, it is also the probability density of  relative to
relative to 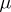 .
.
A concept closely related to the probability density is that of a dominated family of distributions. A family of probability distributions 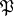 on a measurable space
on a measurable space 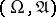 is called dominated if there exists a
is called dominated if there exists a 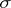 -finite measure
-finite measure 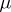 on
on 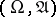 such that each probability measure from
such that each probability measure from 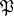 has a probability density relative to
has a probability density relative to 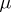 (or, what is the same, if each measure from
(or, what is the same, if each measure from 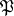 is absolutely continuous with respect to
is absolutely continuous with respect to 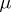 ). The assumption of dominance is important in certain theorems in mathematical statistics.
). The assumption of dominance is important in certain theorems in mathematical statistics.
References
| [1] | Yu.V. [Yu.V. Prokhorov] Prohorov, Yu.A. Rozanov, "Probability theory, basic concepts. Limit theorems, random processes", Springer (1969) (Translated from Russian) |
| [2] | W. Feller, "An introduction to probability theory and its applications", 2, Wiley (1971) |
| [3] | E.L. Lehmann, "Testing statistical hypotheses", Wiley (1986) |
Density of a probability distribution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Density_of_a_probability_distribution&oldid=25939