Difference between revisions of "Fejér sum"
From Encyclopedia of Mathematics
Ulf Rehmann (talk | contribs) |
Ulf Rehmann (talk | contribs) |
(No difference)
| |
Revision as of 07:54, 26 March 2012
One of the arithmetic means of the partial sums of a Fourier series in the trigonometric system
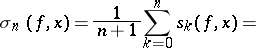 |
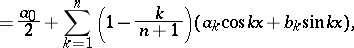 |
where 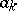 and
and 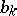 are the Fourier coefficients of the function
are the Fourier coefficients of the function 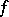 .
.
If 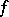 is continuous, then
is continuous, then 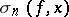 converges uniformly to
converges uniformly to  ;
; 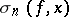 converges to
converges to 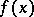 in the metric of
in the metric of 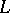 .
.
If 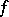 belongs to the class of functions that satisfy a Lipschitz condition of order
belongs to the class of functions that satisfy a Lipschitz condition of order 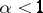 , then
, then
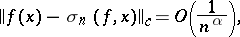 |
that is, in this case the Fejér sum approximates 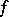 at the rate of the best approximating functions of the indicated class. But Fejér sums cannot provide a high rate of approximation: The estimate
at the rate of the best approximating functions of the indicated class. But Fejér sums cannot provide a high rate of approximation: The estimate
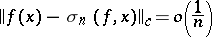 |
is valid only for constant functions.
Fejér sums were introduced by L. Fejér [1].
References
| [1] | L. Fejér, "Untersuchungen über Fouriersche Reihen" Math. Ann. , 58 (1903) pp. 51–69 |
| [2] | N.I. [N.I. Akhiezer] Achiezer, "Theory of approximation" , F. Ungar (1956) (Translated from Russian) |
| [3] | A. Zygmund, "Trigonometric series" , 1–2 , Cambridge Univ. Press (1988) |
| [4] | I.P. Natanson, "Constructive function theory" , 1–3 , F. Ungar (1964–1965) (Translated from Russian) |
| [5] | V.M. Tikhomirov, "Some problems in approximation theory" , Moscow (1976) (In Russian) |
Comments
See also Fejér summation method.
How to Cite This Entry:
Fejér sum. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fej%C3%A9r_sum&oldid=23270
Fejér sum. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fej%C3%A9r_sum&oldid=23270
This article was adapted from an original article by S.A. Telyakovskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article