Difference between revisions of "Tangent line"
| Line 7: | Line 7: | ||
$ | $ | ||
| − | |||
| − | Not every continuous curve has a tangent, since $MM_1$ need not tend to a limiting position at all, or it may tend to two distinct limiting positions as $M_1$ tends to $M$ from different sides of $L$ (Fig. 2). If a curve in the plane with rectangular coordinates is defined by the equation $y=f(x)$ and $f$ is differentiable at the point $x_0$, then the slope of the tangent at $M$ is equal to the value of the derivative $f^\prime(x_0)$ at $x_0$; the equation of the tangent at this point has the form | + | <span id="Fig1"> |
| + | [[File:Tangent-line-1.png| right| frame| Figure 1. The tangent $MT$ (in red) to the line $L$ at the point $M$ ([[Media:Tangent-line.pdf|pdf]]) ]] | ||
| + | </span> | ||
| + | A straight line representing the limiting position of the secants. Let $M$ be a point on a curve $L$ ([[#Fig1|Fig. 1]]). A second point $M_1$ is chosen on $L$ and the straight line $M_1$ is drawn. The point $M$ is regarded as fixed, and $M_1$ approaches $M$ along the curve $L$. If, as $M_1$ goes to $M$, the line $MM_1$ tends to a limiting line $MT$, then $MT$ is called the tangent to $L$ at $M$. | ||
| + | |||
| + | <span id="Fig2"> | ||
| + | [[File:Tangent-line-2.png| right| frame| Figure 2. A point $M$ on a curve $L$ without a tangent([[Media:Tangent-line.pdf|pdf]]) ]] | ||
| + | </span> | ||
| + | Not every continuous curve has a tangent, since $MM_1$ need not tend to a limiting position at all, or it may tend to two distinct limiting positions as $M_1$ tends to $M$ from different sides of $L$ ([[#Fig2|Fig. 2]]). If a curve in the plane with rectangular coordinates is defined by the equation $y=f(x)$ and $f$ is differentiable at the point $x_0$, then the slope of the tangent at $M$ is equal to the value of the derivative $f^\prime(x_0)$ at $x_0$; the equation of the tangent at this point has the form | ||
$$ | $$ | ||
y - f(x_0) = f^\prime(x_0)(x - x_0). | y - f(x_0) = f^\prime(x_0)(x - x_0). | ||
| Line 20: | Line 27: | ||
$$ | $$ | ||
| − | By a tangent to a surface $S$ at a point $M$ one means a straight line passing through $M$ and lying in the [[Tangent plane|tangent plane]]to $S$ at $M$. | + | By a tangent to a surface $S$ at a point $M$ one means a straight line passing through $M$ and lying in the [[Tangent plane|tangent plane]] to $S$ at $M$. |
====References==== | ====References==== | ||
Revision as of 19:37, 24 April 2012
to a curve
$
\newcommand{\vect}[1]{\mathbf{#1}}
$
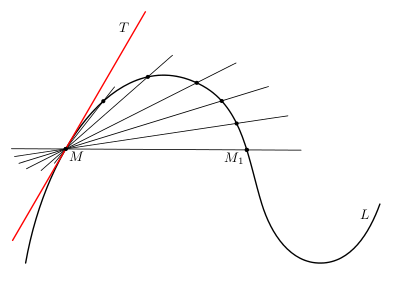
A straight line representing the limiting position of the secants. Let $M$ be a point on a curve $L$ (Fig. 1). A second point $M_1$ is chosen on $L$ and the straight line $M_1$ is drawn. The point $M$ is regarded as fixed, and $M_1$ approaches $M$ along the curve $L$. If, as $M_1$ goes to $M$, the line $MM_1$ tends to a limiting line $MT$, then $MT$ is called the tangent to $L$ at $M$.
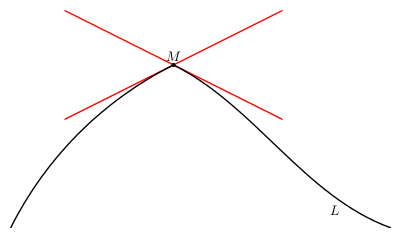
Not every continuous curve has a tangent, since $MM_1$ need not tend to a limiting position at all, or it may tend to two distinct limiting positions as $M_1$ tends to $M$ from different sides of $L$ (Fig. 2). If a curve in the plane with rectangular coordinates is defined by the equation $y=f(x)$ and $f$ is differentiable at the point $x_0$, then the slope of the tangent at $M$ is equal to the value of the derivative $f^\prime(x_0)$ at $x_0$; the equation of the tangent at this point has the form $$ y - f(x_0) = f^\prime(x_0)(x - x_0). $$ The equation of the tangent to a curve $\vect{r} = \vect{r}(t)$ in space is $$ \vect{t}(\lambda) = \vect{r} + \lambda \frac{\mathrm{d}\vect{r}}{\mathrm{d}t}, \quad \lambda \in \R. $$
By a tangent to a surface $S$ at a point $M$ one means a straight line passing through $M$ and lying in the tangent plane to $S$ at $M$.
References
| [BeGo] | M. Berger, B. Gostiaux, "Differential geometry: manifolds, curves, and surfaces", Springer (1988) (Translated from French) |
| [Co] | H.S.M. Coxeter, "Introduction to geometry", Wiley (1961) |
| [Gu] | H.W. Guggenheimer, "Differential geometry", McGraw-Hill (1963) |
| [HiCo] | D. Hilbert, S.E. Cohn-Vossen, "Geometry and the imagination", Chelsea (1952) (Translated from German) |
Tangent line. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Tangent_line&oldid=25289