Difference between revisions of "Pythagorean theorem"
m (moved Pythagoras' theorem to Pythagorean theorem: Name more commonly used) |
(Revised text to exhibit the more common name "the Pythagorean theorem.") |
||
| Line 1: | Line 1: | ||
| − | + | Also known as Pythagoras' theorem, the Pythagorean theorem is a theorem in geometry that gives a relationship between the sides of a right-angled triangle. The Pythagorean theorem was evidently known before Pythagoras (6th century B.C.), but the proof in general form is ascribed to him. Originally the theorem established a relationship between the areas of the squares constructed on the sides of a right-angled triangle: The square on the hypotenuse is equal to the sum of the squares on the other sides. Sometimes, the Pythagorean theorem is formulated briefly as follows: The square of the hypotenuse of a right-angled triangle is equal to the sum of the squares of the catheti. The theorem converse to the Pythagorean theorem is also true: If the square of a side of a triangle is equal to the sum of the squares of the other two sides, then that triangle is right-angled. | |
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | + | The Pythagorean theorem is a special case of the [[Cosine theorem|cosine theorem]]; its infinite-dimensional analogue (in [[Hilbert space|Hilbert space]]) is the [[Parseval equality|Parseval equality]] (i.e. the completeness theorem for orthonormal systems). | |
The problem of solving Phytagoras' equation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075940/p0759401.png" /> in integers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075940/p0759402.png" /> leads to the [[Pythagorean numbers|Pythagorean numbers]]. The problem of solving its generalization, the Diophantine equation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075940/p0759403.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075940/p0759404.png" />, is called Fermat's last (or great) theorem, cf. [[Fermat great theorem|Fermat great theorem]]. | The problem of solving Phytagoras' equation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075940/p0759401.png" /> in integers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075940/p0759402.png" /> leads to the [[Pythagorean numbers|Pythagorean numbers]]. The problem of solving its generalization, the Diophantine equation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075940/p0759403.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075940/p0759404.png" />, is called Fermat's last (or great) theorem, cf. [[Fermat great theorem|Fermat great theorem]]. | ||
Revision as of 06:04, 28 March 2011
Also known as Pythagoras' theorem, the Pythagorean theorem is a theorem in geometry that gives a relationship between the sides of a right-angled triangle. The Pythagorean theorem was evidently known before Pythagoras (6th century B.C.), but the proof in general form is ascribed to him. Originally the theorem established a relationship between the areas of the squares constructed on the sides of a right-angled triangle: The square on the hypotenuse is equal to the sum of the squares on the other sides. Sometimes, the Pythagorean theorem is formulated briefly as follows: The square of the hypotenuse of a right-angled triangle is equal to the sum of the squares of the catheti. The theorem converse to the Pythagorean theorem is also true: If the square of a side of a triangle is equal to the sum of the squares of the other two sides, then that triangle is right-angled.
Comments
The Pythagorean theorem is a special case of the cosine theorem; its infinite-dimensional analogue (in Hilbert space) is the Parseval equality (i.e. the completeness theorem for orthonormal systems).
The problem of solving Phytagoras' equation  in integers
in integers  leads to the Pythagorean numbers. The problem of solving its generalization, the Diophantine equation
leads to the Pythagorean numbers. The problem of solving its generalization, the Diophantine equation 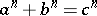 ,
, 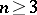 , is called Fermat's last (or great) theorem, cf. Fermat great theorem.
, is called Fermat's last (or great) theorem, cf. Fermat great theorem.
A right-angled triangle with sides having integer lengths is called a Phytagorean triangle.
References
| [a1] | W.H. Greub, "Linear algebra" , Springer (1967) |
Pythagorean theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pythagorean_theorem&oldid=19344