Difference between revisions of "Component of a space"
From Encyclopedia of Mathematics
m |
m |
||
| Line 1: | Line 1: | ||
| − | A connected subset <math>C</math> of a topological space <math>X</math> with the following property: If <math>C_1 \subset X</math> is a connected subset such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c024/c024240/c0242404.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c024/c024240/c0242405.png" />. The components of a space are disjoint. Every non-empty connected subset is contained in exactly one component. If <math>C</math> is a component of a space <math>X</math> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c024/c024240/c0242408.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c024/c024240/c0242409.png" /> is a component of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c024/c024240/c02424010.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c024/c024240/c02424011.png" /> is a monotone continuous mapping onto, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c024/c024240/c02424012.png" /> is a component of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c024/c024240/c02424013.png" /> if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c024/c024240/c02424014.png" /> is a component of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c024/c024240/c02424015.png" />. | + | A connected subset <math> C </math> of a topological space <math> X </math> with the following property: If <math>C_1 \subset X</math> is a connected subset such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c024/c024240/c0242404.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c024/c024240/c0242405.png" />. The components of a space are disjoint. Every non-empty connected subset is contained in exactly one component. If <math> C </math> is a component of a space <math> X </math> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c024/c024240/c0242408.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c024/c024240/c0242409.png" /> is a component of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c024/c024240/c02424010.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c024/c024240/c02424011.png" /> is a monotone continuous mapping onto, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c024/c024240/c02424012.png" /> is a component of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c024/c024240/c02424013.png" /> if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c024/c024240/c02424014.png" /> is a component of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c024/c024240/c02424015.png" />. |
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> K. Kuratowski, "Topology" , '''2''' , Acad. Press (1968) (Translated from French)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> K. Kuratowski, "Topology" , '''2''' , Acad. Press (1968) (Translated from French)</TD></TR></table> | ||
Revision as of 20:37, 25 March 2011
A connected subset \( C \) of a topological space \( X \) with the following property: If \(C_1 \subset X\) is a connected subset such that 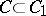 , then
, then 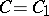 . The components of a space are disjoint. Every non-empty connected subset is contained in exactly one component. If \( C \) is a component of a space \( X \) and
. The components of a space are disjoint. Every non-empty connected subset is contained in exactly one component. If \( C \) is a component of a space \( X \) and 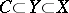 , then
, then 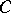 is a component of
is a component of 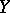 . If
. If  is a monotone continuous mapping onto, then
is a monotone continuous mapping onto, then 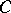 is a component of
is a component of 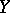 if and only if
if and only if 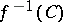 is a component of
is a component of 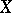 .
.
References
| [1] | K. Kuratowski, "Topology" , 2 , Acad. Press (1968) (Translated from French) |
How to Cite This Entry:
Component of a space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Component_of_a_space&oldid=19329
Component of a space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Component_of_a_space&oldid=19329
This article was adapted from an original article by B.A. Efimov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article