Difference between revisions of "Akivis algebra"
(Importing text file) |
m (link) |
||
| Line 1: | Line 1: | ||
| − | A [[Vector space|vector space]] over a [[Field|field]] with an anti-symmetric bilinear multiplication <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110450/a1104501.png" /> and a multilinear ternary operation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110450/a1104502.png" /> which are linked by the so-called Akivis condition, defined as follows [[#References|[a4]]], [[#References|[a5]]]. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110450/a1104503.png" /> denote the group of all six permutations and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110450/a1104504.png" /> the subgroup of all three cyclic permutations of the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110450/a1104505.png" />. Define <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110450/a1104506.png" />. The Akivis condition reads: | + | A [[Vector space|vector space]] over a [[Field|field]] with an anti-symmetric bilinear multiplication <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110450/a1104501.png" /> and a multilinear [[ternary operation]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110450/a1104502.png" /> which are linked by the so-called Akivis condition, defined as follows [[#References|[a4]]], [[#References|[a5]]]. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110450/a1104503.png" /> denote the group of all six permutations and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110450/a1104504.png" /> the subgroup of all three cyclic permutations of the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110450/a1104505.png" />. Define <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110450/a1104506.png" />. The Akivis condition reads: |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110450/a1104507.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110450/a1104507.png" /></td> </tr></table> | ||
Revision as of 18:02, 21 November 2014
A vector space over a field with an anti-symmetric bilinear multiplication 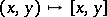 and a multilinear ternary operation
and a multilinear ternary operation 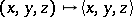 which are linked by the so-called Akivis condition, defined as follows [a4], [a5]. Let
which are linked by the so-called Akivis condition, defined as follows [a4], [a5]. Let 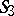 denote the group of all six permutations and
denote the group of all six permutations and 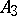 the subgroup of all three cyclic permutations of the set
the subgroup of all three cyclic permutations of the set  . Define
. Define 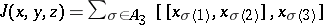 . The Akivis condition reads:
. The Akivis condition reads:
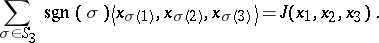 |
The specialization 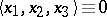 yields a Lie algebra. If
yields a Lie algebra. If 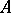 is an arbitrary non-associative algebra over a field with a binary bilinear multiplication
is an arbitrary non-associative algebra over a field with a binary bilinear multiplication 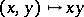 (cf. also Non-associative rings and algebras), then
(cf. also Non-associative rings and algebras), then 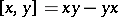 and
and 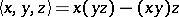 define an Akivis algebra on
define an Akivis algebra on 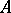 . The tangent algebra of a local analytic loop (cf. Loop, analytic) is always an Akivis algebra. This generalizes the facts that the tangent algebra of a local Lie group (cf. also Lie group, local) is a Lie algebra and that the tangent algebra of a local Moufang loop is a Mal'tsev algebra. Analytic or differentiable quasi-groups (cf. Quasi-group) and loops arise in the study of the geometry of webs (cf. Web), [a2], [a3], [a5].
. The tangent algebra of a local analytic loop (cf. Loop, analytic) is always an Akivis algebra. This generalizes the facts that the tangent algebra of a local Lie group (cf. also Lie group, local) is a Lie algebra and that the tangent algebra of a local Moufang loop is a Mal'tsev algebra. Analytic or differentiable quasi-groups (cf. Quasi-group) and loops arise in the study of the geometry of webs (cf. Web), [a2], [a3], [a5].
References
| [a1] | M.A. Akivis, "The canonical expansions of the equations of a local analytic quasigroup" Soviet Math. Dokl. , 10 (1969) pp. 1200–1203 Dokl. Akad. Nauk SSSR , 188 (1969) pp. 967–970 |
| [a2] | V.V. Goldberg, "Local differentiable quasigroups and webs" O. Chein (ed.) H.O. Pflugfelder (ed.) J.D.H. Smith (ed.) , Quasigroups and Loops - Theory and Applications , Heldermann (1990) pp. 263–311 |
| [a3] | V.V. Goldberg, "Theory of multicodimensional 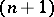 -webs" , Kluwer Acad. Publ. (1988) -webs" , Kluwer Acad. Publ. (1988) |
| [a4] | K.H. Hofmann, K. Strambach, "The Akivis algebra of a homogeneous loop" Mathematika , 33 (1986) pp. 87–95 |
| [a5] | K.H. Hofmann, K. Strambach, "Topological and analytic loops" O. Chein (ed.) H.O. Pflugfelder (ed.) J.D.H. Smith (ed.) , Quasigroups and Loops - Theory and Applications , Heldermann (1990) pp. 205–262 |
| [a6] | P.O. Miheev, L.V. Sabinin, "Quasigroups and differential geometry" O. Chein (ed.) H.O. Pflugfelder (ed.) J.D.H. Smith (ed.) , Quasigroups and Loops - Theory and Applications , Heldermann (1990) pp. 357–430 |
Akivis algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Akivis_algebra&oldid=19133