Difference between revisions of "Point of inflection"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | A | + | <!-- |
| + | p0731901.png | ||
| + | $#A+1 = 27 n = 0 | ||
| + | $#C+1 = 27 : ~/encyclopedia/old_files/data/P073/P.0703190 Point of inflection | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
| + | A point $ M $ | ||
| + | on a planar curve having the following properties: at $ M $ | ||
| + | the curve has a unique tangent, and within a small neighbourhood around $ M $ | ||
| + | the curve lies within one pair of vertical angles formed by the tangent and the normal (Fig. a). normal tangent | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/p073190a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/p073190a.gif" /> | ||
| Line 5: | Line 20: | ||
Figure: p073190a | Figure: p073190a | ||
| − | Let a function | + | Let a function $ f $ |
| + | be defined in a certain neighbourhood around a point $ x _ {0} $ | ||
| + | and let it be continuous at that point. The point $ x _ {0} $ | ||
| + | is called a point of inflection for $ f $ | ||
| + | if it is simultaneously the end of a range of strict convexity upwards and the end of a range of strict convexity downwards. In that case the point $ ( x _ {0} , f( x _ {0} )) $ | ||
| + | is called a point of inflection on the graph of the function, i.e. the graph of $ f $ | ||
| + | at $ ( x _ {0} , f( x _ {0} )) $" | ||
| + | inflects" through the tangent to it at that point; for $ x < x _ {0} $ | ||
| + | the tangent lies under the graph of $ f $, | ||
| + | while for $ x > x _ {0} $ | ||
| + | it lies above that graph (or vice versa, Fig. b). | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/p073190b.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/p073190b.gif" /> | ||
| Line 11: | Line 36: | ||
Figure: p073190b | Figure: p073190b | ||
| − | A necessary existence condition for a point of inflection is: If | + | A necessary existence condition for a point of inflection is: If $ f $ |
| + | is twice differentiable in some neighbourhood of a point $ x _ {0} $, | ||
| + | and if $ x _ {0} $ | ||
| + | is a point of inflection, then $ f ^ { \prime\prime } ( x _ {0} ) = 0 $. | ||
| + | A sufficient existence condition for a point of inflection is: If $ f $ | ||
| + | is $ k $ | ||
| + | times continuously differentiable in a certain neighbourhood of a point $ x $, | ||
| + | with $ k $ | ||
| + | odd and $ k \geq 3 $, | ||
| + | while $ f ^ { ( n) } ( x _ {0} ) = 0 $ | ||
| + | for $ n = 2 \dots k- 1 $, | ||
| + | and $ f ^ { ( k) } ( x _ {0} ) \neq 0 $, | ||
| + | then $ f $ | ||
| + | has a point of inflection at $ x _ {0} $. | ||
====References==== | ====References==== | ||
| Line 17: | Line 55: | ||
====Comments==== | ====Comments==== | ||
| − | |||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> M. Berger, B. Gostiaux, "Differential geometry: manifolds, curves, and surfaces" , Springer (1988) (Translated from French)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J.L. Coolidge, "Algebraic plane curves" , Dover, reprint (1959)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> M. Berger, B. Gostiaux, "Differential geometry: manifolds, curves, and surfaces" , Springer (1988) (Translated from French)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J.L. Coolidge, "Algebraic plane curves" , Dover, reprint (1959)</TD></TR></table> | ||
Latest revision as of 08:06, 6 June 2020
A point $ M $
on a planar curve having the following properties: at $ M $
the curve has a unique tangent, and within a small neighbourhood around $ M $
the curve lies within one pair of vertical angles formed by the tangent and the normal (Fig. a). normal tangent
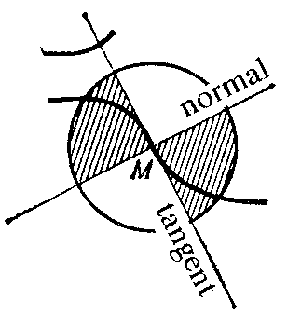
Figure: p073190a
Let a function $ f $ be defined in a certain neighbourhood around a point $ x _ {0} $ and let it be continuous at that point. The point $ x _ {0} $ is called a point of inflection for $ f $ if it is simultaneously the end of a range of strict convexity upwards and the end of a range of strict convexity downwards. In that case the point $ ( x _ {0} , f( x _ {0} )) $ is called a point of inflection on the graph of the function, i.e. the graph of $ f $ at $ ( x _ {0} , f( x _ {0} )) $" inflects" through the tangent to it at that point; for $ x < x _ {0} $ the tangent lies under the graph of $ f $, while for $ x > x _ {0} $ it lies above that graph (or vice versa, Fig. b).
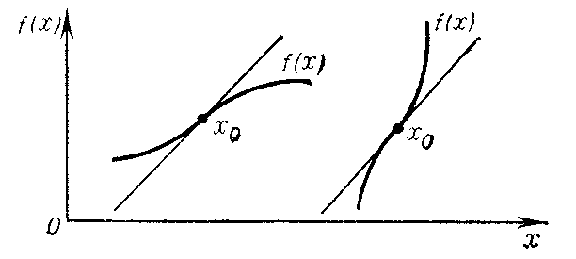
Figure: p073190b
A necessary existence condition for a point of inflection is: If $ f $ is twice differentiable in some neighbourhood of a point $ x _ {0} $, and if $ x _ {0} $ is a point of inflection, then $ f ^ { \prime\prime } ( x _ {0} ) = 0 $. A sufficient existence condition for a point of inflection is: If $ f $ is $ k $ times continuously differentiable in a certain neighbourhood of a point $ x $, with $ k $ odd and $ k \geq 3 $, while $ f ^ { ( n) } ( x _ {0} ) = 0 $ for $ n = 2 \dots k- 1 $, and $ f ^ { ( k) } ( x _ {0} ) \neq 0 $, then $ f $ has a point of inflection at $ x _ {0} $.
References
| [1] | V.A. Il'in, E.G. Poznyak, "Fundamentals of mathematical analysis" , 2 , MIR (1982) (Translated from Russian) |
| [2] | L.D. Kudryavtsev, "A course in mathematical analysis" , 1 , Moscow (1981) (In Russian) |
Comments
References
| [a1] | M. Berger, B. Gostiaux, "Differential geometry: manifolds, curves, and surfaces" , Springer (1988) (Translated from French) |
| [a2] | J.L. Coolidge, "Algebraic plane curves" , Dover, reprint (1959) |
Point of inflection. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Point_of_inflection&oldid=14389