Difference between revisions of "Elliptic surface"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
m (fixing superscripts) |
||
| (One intermediate revision by one other user not shown) | |||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | e0355501.png | ||
| + | $#A+1 = 180 n = 2 | ||
| + | $#C+1 = 180 : ~/encyclopedia/old_files/data/E035/E.0305550 Elliptic surface | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | An algebraic or analytic complete non-singular surface $ X $ | |
| + | having a fibration of elliptic curves (cf. [[Elliptic curve|Elliptic curve]]), that is, a morphism $ \pi : X \rightarrow B $ | ||
| + | onto a non-singular curve $ B $ | ||
| + | whose generic fibre is a non-singular elliptic curve. Every elliptic surface is birationally (bimeromorphically) equivalent over $ B $ | ||
| + | to a unique minimal model, which is characterized by the fact that the fibre of $ \pi $ | ||
| + | does not contain exceptional curves of arithmetic genus 1. In what follows an elliptic surface is assumed to be minimal. Minimal elliptic surfaces have a more complicated structure than ruled surfaces. They can have singular fibres $ X _ {t} = \pi ^ {- 1} ( t) $ (that is, fibres that are not non-singular elliptic curves). There is a classification | ||
| − | + | of the singular fibres of elliptic surfaces. A singular fibre $ X _ {t} = \sum n _ {i} E _ {i} $ | |
| + | is called multiple if the greatest common divisor of the $ n _ {i} $ | ||
| + | is $ m \geq 2 $, | ||
| + | and then $ X _ {t} = m F $ | ||
| + | and $ m $ | ||
| + | is called the multiplicity of the fibre $ X _ {t} $. | ||
| − | + | On a minimal elliptic surface the canonical class $ K _ {X} $ | |
| + | contains a divisor that is a rational combination of fibres, in particular, $ ( K _ {X} ^ {2} ) = 0 $. | ||
| + | Moreover, the following formula holds for the canonical class (see [[#References|[1]]], ): | ||
| − | + | $$ | |
| + | K _ {X} = \pi ^ {*} ( K _ {B} - d ) + | ||
| + | \sum ( m _ {i} - 1 ) F _ {i} , | ||
| + | $$ | ||
| + | |||
| + | where $ X _ {t _ {i} } = m _ {i} F _ {i} $ | ||
| + | are all the multiple fibres of $ \pi $ | ||
| + | and $ d $ | ||
| + | is a divisor on $ B $ | ||
| + | of degree $ - \chi ( {\mathcal O} _ {X} ) $. | ||
| + | The topological [[Euler characteristic|Euler characteristic]] satisfies the formula | ||
| + | |||
| + | $$ | ||
| + | e ( X) = \sum e ( X _ {t _ {i} } ) . | ||
| + | $$ | ||
==The classification of elliptic fibrations.== | ==The classification of elliptic fibrations.== | ||
| − | A fibration | + | A fibration $ \pi : X \rightarrow B $ |
| + | can be regarded as an elliptic curve over the function field $ k ( B) $. | ||
| + | This curve, generally speaking, does not have the structure of an Abelian variety over $ k ( B) $. | ||
| + | For this to happen it is necessary that it has a rational point over $ k ( B) $ (and then $ X $ | ||
| + | is birationally isomorphic to the surface defined in $ B \times A ^ {2} $ | ||
| + | by the Weierstrass equation $ y ^ {2} = x ^ {3} - g _ {2} x - g _ {3} $, | ||
| + | where $ g _ {2} , g _ {3} \in k ( B) $). | ||
| + | The specification of a rational point is equivalent to that of a section $ e : B \rightarrow X $ | ||
| + | such that $ \pi e = \mathop{\rm id} $; | ||
| + | a necessary condition for the existence of a section is the absence of multiple fibres. Fibrations without multiple fibres are called reduced. Every fibration, after a suitable ramified covering of the base, has a section (that is, is reduced) . Every fibration can also be made reduced by a sequence of transformations inverse to logarithmic ones | ||
— local surgery of the fibration in neighbourhoods of fibres. | — local surgery of the fibration in neighbourhoods of fibres. | ||
| − | Reduced elliptic fibrations may be described as follows. To every such fibration | + | Reduced elliptic fibrations may be described as follows. To every such fibration $ \pi : X \rightarrow B $ |
| + | corresponds a unique fibration $ {\mathcal J} _ {B} ( X) \rightarrow B $ | ||
| + | that is a [[Group object|group object]] and is such that $ X / B $ | ||
| + | is a [[Principal homogeneous space|principal homogeneous space]] over $ {\mathcal J} _ {B} ( X) / B $; | ||
| + | $ {\mathcal J} _ {B} ( X) / B $ | ||
| + | is the Jacobi fibration for $ X / B $; | ||
| + | it characterizes the existence of a section. For a given Jacobi fibration $ {\mathcal J} / B $, | ||
| + | the set $ I ( {\mathcal J} / B ) $ | ||
| + | of isomorphism classes of fibrations $ X / B $ | ||
| + | for which $ {\mathcal J} _ {B} ( X) \cong J $ | ||
| + | has a cohomology description analogous to that of invertible sheaves (cf. [[Invertible sheaf|Invertible sheaf]]). Here the role of $ {\mathcal O} _ {B} ^ {*} $ | ||
| + | is played by the sheaf $ {\mathcal H} ^ {0} ( {\mathcal J} / B ) $ | ||
| + | of local sections $ \tau : {\mathcal J} \rightarrow B $. | ||
| + | There is a natural one-to-one correspondence | ||
| − | + | $$ | |
| + | \theta : I ( {\mathcal J} / B ) \rightarrow H ^ {1} | ||
| + | ( B , {\mathcal H} ^ {0} ( {\mathcal J} / B ) ) , | ||
| + | $$ | ||
| − | under which the Jacobi fibration corresponds to the zero element. By means of | + | under which the Jacobi fibration corresponds to the zero element. By means of $ \theta $ |
| + | one can distinguish between algebraic and non-algebraic fibrations: For a reduced fibration $ \pi : X \rightarrow B $ | ||
| + | the surface $ X $ | ||
| + | is algebraic if and only if the element corresponding to it in $ H ^ {1} ( B , {\mathcal H} ^ {0} ( {\mathcal J} / B )) $ | ||
| + | is of finite order. The analogy with invertible sheaves can be pursued further. The analogue of the exact sequence | ||
| − | + | $$ | |
| + | 0 \rightarrow \mathbf Z \rightarrow {\mathcal O} _ {B} \mathop \rightarrow \limits ^ {\mathop {\rm exp}} {\mathcal O} _ {B} ^ {*} \rightarrow 1 | ||
| + | $$ | ||
is the exact sequence | is the exact sequence | ||
| − | + | $$ | |
| + | 0 \rightarrow R ^ {1} \tau _ {0} \mathbf Z \rightarrow {\mathcal H} ^ {0} | ||
| + | ( T ( {\mathcal J} ) / B ) \rightarrow {\mathcal H} ^ {0} ( {\mathcal J} / B ) \rightarrow 0 , | ||
| + | $$ | ||
| − | where | + | where $ {\mathcal H} ^ {0} ( T ( {\mathcal J} ) / B ) $ |
| + | is the sheaf of local sections of the bundle $ T ( {\mathcal J} )/ B $ | ||
| + | and $ T ( {\mathcal J} ) $ | ||
| + | is the tangent space to the fibre $ \tau ^ {- 1 }( b) $ | ||
| + | at $ e ( b) $. | ||
| + | The boundary homomorphism | ||
| − | + | $$ | |
| + | \delta : H ^ {1} ( B , {\mathcal H} ^ {0} | ||
| + | ( {\mathcal J} / B ) ) \rightarrow H ^ {2} ( B , R ^ {1} \tau _ {*} \mathbf Z ) | ||
| + | $$ | ||
| − | allows one to recognize when one fibration is a deformation of another. For that it is necessary and sufficient that the elements corresponding to these fibrations have one and the same image under | + | allows one to recognize when one fibration is a deformation of another. For that it is necessary and sufficient that the elements corresponding to these fibrations have one and the same image under $ \delta $ (see ). |
==The classification of algebraic elliptic surfaces.== | ==The classification of algebraic elliptic surfaces.== | ||
| − | Suppose that | + | Suppose that $ \mathop{\rm char} k = 0 $. |
| + | For an elliptic surface $ X $ | ||
| + | the canonical dimension $ k ( X) \leq 1 $, | ||
| + | that is, it is equal to $ - 1 $, | ||
| + | 0 or $ 1 $. | ||
| + | If $ k ( X) = 1 $, | ||
| + | $ X $ | ||
| + | is said to be an elliptic surface of general type. These are characterized by the conditions $ 12 K _ {X} \neq 0 $ | ||
| + | and $ | 12 K _ {X} | \neq \emptyset $. | ||
| + | Elliptic surfaces with $ p _ {g} \geq 2 $ | ||
| + | or, more generally, with $ P _ {m} \geq 2 $ | ||
| + | for some $ m $, | ||
| + | are of general type. | ||
| − | Elliptic surfaces with | + | Elliptic surfaces with $ k ( X) = 0 $ |
| + | are characterized by the condition $ 12 K _ {X} = 0 $. | ||
| + | In this case $ \chi ( {\mathcal O} _ {X} ) $ | ||
| + | can take the three values 2, 1 or $ 0 $. | ||
| + | If $ \chi ( {\mathcal O} _ {X} )= 2 $, | ||
| + | then $ X $ | ||
| + | is an elliptic [[K3-surface| $ K 3 $-surface]] ( $ q = 0 $, | ||
| + | $ K _ {X} = 0 $). | ||
| + | In this case $ B $ | ||
| + | is isomorphic to the projective line $ P ^ {1} $, | ||
| + | the fibration has no multiple fibres and $ X $ | ||
| + | has the invariants $ p _ {g} = 1 $, | ||
| + | $ q = 0 $, | ||
| + | $ b _ {2} = 22 $. | ||
| + | If $ \chi ( {\mathcal O} _ {X} ) = 1 $, | ||
| + | then $ X $ | ||
| + | is an Enriques surface, that is, a surface with $ p _ {g} = q = 0 $, | ||
| + | $ 2 K _ {X} = 0 $. | ||
| + | (Every Enriques surface is elliptic.) In this case $ B \simeq P ^ {1} $, | ||
| + | the fibration has two fibres of multiplicity 2, and $ X $ | ||
| + | has the invariants $ p _ {g} = q = 0 $, | ||
| + | $ b _ {2} = 10 $. | ||
| + | If $ \chi ( {\mathcal O} _ {X} ) = 0 $, | ||
| + | then two cases are possible. Either $ X $ | ||
| + | is an Abelian variety (and then $ p _ {g} = 1 $, | ||
| + | $ q = 2 $, | ||
| + | $ b _ {2} = 6 $); | ||
| + | or $ X $ | ||
| + | is a hyper-elliptic surface, that is, a surface that has a finite unramified covering — the product of two elliptic curves. In that case $ p _ {g} = 0 $, | ||
| + | $ b _ {1} = 2 $, | ||
| + | $ b _ {2} = 2 $, | ||
| + | $ B = P ^ {1} $, | ||
| + | and $ \pi $ | ||
| + | has 3 or 4 multiple fibres with four possibilities for their multiplicity: $ ( 3 , 3 , 3 ) $, | ||
| + | $ ( 2 , 4 , 4 ) $, | ||
| + | $ ( 2 , 3 , 6 ) $, | ||
| + | and $ ( 2 , 2 , 2 , 2 ) $, | ||
| + | and $ 3 K _ {X} = 0 $, | ||
| + | $ 4 K _ {X} = 0 $, | ||
| + | $ 6 K _ {X} = 0 $, | ||
| + | and $ 2 K _ {X} = 0 $, | ||
| + | respectively. | ||
| − | An elliptic surface with | + | An elliptic surface with $ k ( X) = - 1 $ |
| + | is ruled (cf. [[Ruled surface|Ruled surface]]). It is characterized by the condition $ | 12 K _ {X} | = \emptyset $. | ||
| + | Here two cases are possible: 1) $ X $ | ||
| + | is a surface with $ p _ {g} = q = 0 $, | ||
| + | $ b _ {2} = 10 $, | ||
| + | and $ \pi $ | ||
| + | has no multiple fibres or one; moreover, a surface without multiple fibres can be obtained as follows: one has to take a rational mapping $ P ^ {2} \rightarrow P ^ {1} $ | ||
| + | determined by two cubics $ F _ {0} $ | ||
| + | and $ F _ {1} $ | ||
| + | and blow up their 9 points of intersection; or 2) $ X $ | ||
| + | is a surface with $ p _ {g} = 0 $, | ||
| + | $ q = 1 $, | ||
| + | $ b _ {2} = 2 $, | ||
| + | and the multiplicities $ m _ {i} $ | ||
| + | are subject to the inequality | ||
| − | + | $$ | |
| + | \sum \left ( 1 - | ||
| + | \frac{1}{m _ {i} } | ||
| + | \right ) < 2 . | ||
| + | $$ | ||
The formula for the canonical class and the classification of elliptic surfaces can also be generalized to the case of a field of finite characteristic [[#References|[5]]], [[#References|[6]]]. | The formula for the canonical class and the classification of elliptic surfaces can also be generalized to the case of a field of finite characteristic [[#References|[5]]], [[#References|[6]]]. | ||
==The classification of non-algebraic elliptic surfaces.== | ==The classification of non-algebraic elliptic surfaces.== | ||
| − | The classification of non-algebraic elliptic surfaces. For non-algebraic surfaces the algebraic dimension | + | The classification of non-algebraic elliptic surfaces. For non-algebraic surfaces the algebraic dimension $ a ( X) = \mathop{\rm tr} \mathop{\rm deg} M ( X) $ |
| + | is 1 or 0. If $ a ( X) = 0 $, | ||
| + | then $ X $ | ||
| + | is non-elliptic. All surfaces with $ a ( X) = 1 $ | ||
| + | are elliptic. Here the structure of $ \pi : X \rightarrow B $ | ||
| + | is determined almost canonically: Every such fibration $ \pi $ | ||
| + | is necessarily elliptic. The classification by the canonical dimension is precisely the same as for algebraic elliptic surfaces: $ k ( X) = - 1 $ | ||
| + | $ \iff $ | ||
| + | $ | 12 K _ {X} | = \emptyset $; | ||
| + | $ k ( X) = 0 $ | ||
| + | $ \iff $ | ||
| + | $ 12K _ {X} = 0 $; | ||
| + | and $ k ( X) = 1 $ ($ X $ | ||
| + | is of basic type) $ \iff $ | ||
| + | $ | 12 K _ {X} | = \emptyset $, | ||
| + | $ 12 K _ {X} \neq 0 $. | ||
| − | Non-algebraic elliptic surfaces with | + | Non-algebraic elliptic surfaces with $ k ( X) = 0 $ |
| + | belong to one of the following classes: 1) the $ K 3 $-surfaces ( $ \chi ( {\mathcal O} _ {X} )= 2 $, | ||
| + | $ b _ {1} = 0 $, | ||
| + | $ b _ {2} = 22 $, | ||
| + | $ X $ | ||
| + | is simply connected); 2) the complex tori ( $ K _ {X} = 0 $, | ||
| + | $ \chi ( {\mathcal O} _ {X} ) = 0 $, | ||
| + | $ b _ {1} = 4 $, | ||
| + | $ b _ {2} = 6 $); | ||
| + | 3) the Kodaira surfaces ( $ K _ {X} = 0 $, | ||
| + | $ \chi ( {\mathcal O} _ {X} ) = 0 $, | ||
| + | $ b _ {1} = 3 $, | ||
| + | $ b _ {2} = 4 $). | ||
| + | Primary Kodaira surfaces are holomorphically locally trivial fibrations over an elliptic curve with an elliptic curve as typical fibre, and from the point of view of differentiability, bundles over a $ 3 $-dimensional torus with a circle as fibre; or 4) the surfaces with $ \chi ( {\mathcal O} _ {X} ) = 0 $, | ||
| + | $ p _ {g} = 0 $, | ||
| + | $ b _ {1} = 1 $, | ||
| + | $ b _ {2} = 0 $. | ||
| + | For them $ m K _ {X} = 0 $ | ||
| + | with $ m = 2 , 3 , 4 $, | ||
| + | (analogous to hyper-elliptic surfaces). They have Kodaira surfaces as finite unramified coverings. In the cases 2), 3) and 4) $ \mathbf C ^ {2} $ | ||
| + | is the universal covering of $ X $. | ||
| − | Non-algebraic elliptic surfaces with | + | Non-algebraic elliptic surfaces with $ k ( X) = - 1 $ |
| + | are Hopf surfaces, that is, their universal covering is $ \mathbf C ^ {2} \setminus 0 $. | ||
| + | For them $ \chi ( {\mathcal O} _ {X} ) = 0 $, | ||
| + | $ b _ {1} = 1 $, | ||
| + | $ b _ {2} = 0 $. | ||
| + | The proper Hopf surfaces are $ ( \mathbf C ^ {2} \setminus 0 ) / T $, | ||
| + | where $ T ( z _ {1} , z _ {2} ) = ( \alpha _ {1} z _ {1} , \alpha _ {2} z _ {2} ) $ | ||
| + | are real generators of $ T $. | ||
| + | They are homeomorphic to $ S ^ {1} \times S ^ {2} $ | ||
| + | and are characterized by this property. Arbitrary elliptic Hopf surfaces are quotients of proper Hopf surfaces . | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> "Algebraic surfaces" ''Proc. Steklov Inst. Math.'' , '''75''' (1967) ''Trudy Mat. Inst. Steklov.'' , '''75''' (1965) {{MR|}} {{ZBL|0172.37901}} {{ZBL|0153.22401}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> D. Husemoller, "Classification and embeddings of surfaces" R. Hartshorne (ed.) , ''Algebraic geometry (Arcata, 1974)'' , ''Proc. Symp. Pure Math.'' , '''29''' , Amer. Math. Soc. (1982) pp. 329–420 {{MR|0506292}} {{ZBL|0326.14009}} </TD></TR><TR><TD valign="top">[3a]</TD> <TD valign="top"> K. Kodaira, "On compact complex analytic surfaces I" ''Ann. of Math. (2)'' , '''71''' (10) pp. 111–152 {{MR|0132556}} {{ZBL|0137.17501}} {{ZBL|0098.13004}} </TD></TR><TR><TD valign="top">[3b]</TD> <TD valign="top"> K. Kodaira, "On compact complex analytic surfaces II" ''Ann. of Math. (2)'' , '''77''' (1963) pp. 563–626 {{MR|165541}} {{ZBL|0193.37701}} {{ZBL|0133.16505}} </TD></TR><TR><TD valign="top">[3c]</TD> <TD valign="top"> K. Kodaira, "On compact complex analytic surfaces III" ''Ann. of Math. (2)'' , '''78''' (1963) pp. 1–40 {{MR|165541}} {{ZBL|0193.37701}} </TD></TR><TR><TD valign="top">[4a]</TD> <TD valign="top"> K. Kodaira, "On the structure of compact complex analytic surfaces I" ''Amer. J. Math.'' , '''86''' (1964) pp. 751–798 {{MR|0187255}} {{ZBL|0137.17501}} </TD></TR><TR><TD valign="top">[4b]</TD> <TD valign="top"> K. Kodaira, "On the structure of compact complex analytic surfaces II" ''Amer. J. Math.'' , '''88''' (1966) pp. 682–721 {{MR|0205280}} {{ZBL|0193.37701}} </TD></TR><TR><TD valign="top">[4c]</TD> <TD valign="top"> K. Kodaira, "On the structure of compact complex analytic surfaces III" ''Amer. J. Math.'' , '''90''' (1968) pp. 55–83 {{MR|0228019}} {{ZBL|0193.37701}} </TD></TR><TR><TD valign="top">[4d]</TD> <TD valign="top"> K. Kodaira, "On the structure of compact complex analytic surfaces IV" ''Amer. J. Math.'' , '''90''' (1968) pp. 1048–1066 {{MR|239114}} {{ZBL|}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> D. Mumford, "Enriques' classification of surfaces in char <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035550/e035550177.png" />. I" D.C. Spencer (ed.) S. Iyanaga (ed.) , ''Global analysis (papers in honor of K. Kodaira)'' , Princeton Univ. Press (1969) pp. 325–339 {{MR|0491719}} {{MR|0491720}} {{ZBL|}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> E. Bombieri, D. Mumford, "Enriques' classification of surfaces in char <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035550/e035550178.png" />. II" W.L. Baily jr. (ed.) T. Shioda (ed.) , ''Complex Analysis and Algebraic geometry'' , Cambridge Univ. Press & Iwanami Shoten (1977) pp. 23–42 {{MR|0491719}} {{MR|0491720}} {{ZBL|}} </TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> "Algebraic surfaces" ''Proc. Steklov Inst. Math.'' , '''75''' (1967) ''Trudy Mat. Inst. Steklov.'' , '''75''' (1965) {{MR|}} {{ZBL|0172.37901}} {{ZBL|0153.22401}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> D. Husemoller, "Classification and embeddings of surfaces" R. Hartshorne (ed.) , ''Algebraic geometry (Arcata, 1974)'' , ''Proc. Symp. Pure Math.'' , '''29''' , Amer. Math. Soc. (1982) pp. 329–420 {{MR|0506292}} {{ZBL|0326.14009}} </TD></TR><TR><TD valign="top">[3a]</TD> <TD valign="top"> K. Kodaira, "On compact complex analytic surfaces I" ''Ann. of Math. (2)'' , '''71''' (10) pp. 111–152 {{MR|0132556}} {{ZBL|0137.17501}} {{ZBL|0098.13004}} </TD></TR><TR><TD valign="top">[3b]</TD> <TD valign="top"> K. Kodaira, "On compact complex analytic surfaces II" ''Ann. of Math. (2)'' , '''77''' (1963) pp. 563–626 {{MR|165541}} {{ZBL|0193.37701}} {{ZBL|0133.16505}} </TD></TR><TR><TD valign="top">[3c]</TD> <TD valign="top"> K. Kodaira, "On compact complex analytic surfaces III" ''Ann. of Math. (2)'' , '''78''' (1963) pp. 1–40 {{MR|165541}} {{ZBL|0193.37701}} </TD></TR><TR><TD valign="top">[4a]</TD> <TD valign="top"> K. Kodaira, "On the structure of compact complex analytic surfaces I" ''Amer. J. Math.'' , '''86''' (1964) pp. 751–798 {{MR|0187255}} {{ZBL|0137.17501}} </TD></TR><TR><TD valign="top">[4b]</TD> <TD valign="top"> K. Kodaira, "On the structure of compact complex analytic surfaces II" ''Amer. J. Math.'' , '''88''' (1966) pp. 682–721 {{MR|0205280}} {{ZBL|0193.37701}} </TD></TR><TR><TD valign="top">[4c]</TD> <TD valign="top"> K. Kodaira, "On the structure of compact complex analytic surfaces III" ''Amer. J. Math.'' , '''90''' (1968) pp. 55–83 {{MR|0228019}} {{ZBL|0193.37701}} </TD></TR><TR><TD valign="top">[4d]</TD> <TD valign="top"> K. Kodaira, "On the structure of compact complex analytic surfaces IV" ''Amer. J. Math.'' , '''90''' (1968) pp. 1048–1066 {{MR|239114}} {{ZBL|}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> D. Mumford, "Enriques' classification of surfaces in char <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035550/e035550177.png" />. I" D.C. Spencer (ed.) S. Iyanaga (ed.) , ''Global analysis (papers in honor of K. Kodaira)'' , Princeton Univ. Press (1969) pp. 325–339 {{MR|0491719}} {{MR|0491720}} {{ZBL|}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> E. Bombieri, D. Mumford, "Enriques' classification of surfaces in char <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035550/e035550178.png" />. II" W.L. Baily jr. (ed.) T. Shioda (ed.) , ''Complex Analysis and Algebraic geometry'' , Cambridge Univ. Press & Iwanami Shoten (1977) pp. 23–42 {{MR|0491719}} {{MR|0491720}} {{ZBL|}} </TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
A secondary Kodaira surface is a surface other than a primary one, admitting a primary Kodaira surface as an unramified covering. They are elliptic fibrations over a rational curve. Their first Betti number is 1. | A secondary Kodaira surface is a surface other than a primary one, admitting a primary Kodaira surface as an unramified covering. They are elliptic fibrations over a rational curve. Their first Betti number is 1. | ||
| − | The canonical dimension | + | The canonical dimension $ k ( X) $ |
| + | mentioned at the start of the section on classification of algebraic elliptic surfaces is the [[Kodaira dimension|Kodaira dimension]] $ \mathop{\rm Kod} ( X) $ (with $ k ( X) = - 1 $ | ||
| + | if $ \mathop{\rm Kod} ( X) = - \infty $). | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> W. Barth, C. Peters, A. van der Ven, "Compact complex surfaces" , Springer (1984) {{MR|0749574}} {{ZBL|0718.14023}} </TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> W. Barth, C. Peters, A. van der Ven, "Compact complex surfaces" , Springer (1984) {{MR|0749574}} {{ZBL|0718.14023}} </TD></TR></table> | ||
Latest revision as of 05:46, 13 June 2022
An algebraic or analytic complete non-singular surface $ X $
having a fibration of elliptic curves (cf. Elliptic curve), that is, a morphism $ \pi : X \rightarrow B $
onto a non-singular curve $ B $
whose generic fibre is a non-singular elliptic curve. Every elliptic surface is birationally (bimeromorphically) equivalent over $ B $
to a unique minimal model, which is characterized by the fact that the fibre of $ \pi $
does not contain exceptional curves of arithmetic genus 1. In what follows an elliptic surface is assumed to be minimal. Minimal elliptic surfaces have a more complicated structure than ruled surfaces. They can have singular fibres $ X _ {t} = \pi ^ {- 1} ( t) $ (that is, fibres that are not non-singular elliptic curves). There is a classification
of the singular fibres of elliptic surfaces. A singular fibre $ X _ {t} = \sum n _ {i} E _ {i} $ is called multiple if the greatest common divisor of the $ n _ {i} $ is $ m \geq 2 $, and then $ X _ {t} = m F $ and $ m $ is called the multiplicity of the fibre $ X _ {t} $.
On a minimal elliptic surface the canonical class $ K _ {X} $ contains a divisor that is a rational combination of fibres, in particular, $ ( K _ {X} ^ {2} ) = 0 $. Moreover, the following formula holds for the canonical class (see [1], ):
$$ K _ {X} = \pi ^ {*} ( K _ {B} - d ) + \sum ( m _ {i} - 1 ) F _ {i} , $$
where $ X _ {t _ {i} } = m _ {i} F _ {i} $ are all the multiple fibres of $ \pi $ and $ d $ is a divisor on $ B $ of degree $ - \chi ( {\mathcal O} _ {X} ) $. The topological Euler characteristic satisfies the formula
$$ e ( X) = \sum e ( X _ {t _ {i} } ) . $$
The classification of elliptic fibrations.
A fibration $ \pi : X \rightarrow B $ can be regarded as an elliptic curve over the function field $ k ( B) $. This curve, generally speaking, does not have the structure of an Abelian variety over $ k ( B) $. For this to happen it is necessary that it has a rational point over $ k ( B) $ (and then $ X $ is birationally isomorphic to the surface defined in $ B \times A ^ {2} $ by the Weierstrass equation $ y ^ {2} = x ^ {3} - g _ {2} x - g _ {3} $, where $ g _ {2} , g _ {3} \in k ( B) $). The specification of a rational point is equivalent to that of a section $ e : B \rightarrow X $ such that $ \pi e = \mathop{\rm id} $; a necessary condition for the existence of a section is the absence of multiple fibres. Fibrations without multiple fibres are called reduced. Every fibration, after a suitable ramified covering of the base, has a section (that is, is reduced) . Every fibration can also be made reduced by a sequence of transformations inverse to logarithmic ones
— local surgery of the fibration in neighbourhoods of fibres.
Reduced elliptic fibrations may be described as follows. To every such fibration $ \pi : X \rightarrow B $ corresponds a unique fibration $ {\mathcal J} _ {B} ( X) \rightarrow B $ that is a group object and is such that $ X / B $ is a principal homogeneous space over $ {\mathcal J} _ {B} ( X) / B $; $ {\mathcal J} _ {B} ( X) / B $ is the Jacobi fibration for $ X / B $; it characterizes the existence of a section. For a given Jacobi fibration $ {\mathcal J} / B $, the set $ I ( {\mathcal J} / B ) $ of isomorphism classes of fibrations $ X / B $ for which $ {\mathcal J} _ {B} ( X) \cong J $ has a cohomology description analogous to that of invertible sheaves (cf. Invertible sheaf). Here the role of $ {\mathcal O} _ {B} ^ {*} $ is played by the sheaf $ {\mathcal H} ^ {0} ( {\mathcal J} / B ) $ of local sections $ \tau : {\mathcal J} \rightarrow B $. There is a natural one-to-one correspondence
$$ \theta : I ( {\mathcal J} / B ) \rightarrow H ^ {1} ( B , {\mathcal H} ^ {0} ( {\mathcal J} / B ) ) , $$
under which the Jacobi fibration corresponds to the zero element. By means of $ \theta $ one can distinguish between algebraic and non-algebraic fibrations: For a reduced fibration $ \pi : X \rightarrow B $ the surface $ X $ is algebraic if and only if the element corresponding to it in $ H ^ {1} ( B , {\mathcal H} ^ {0} ( {\mathcal J} / B )) $ is of finite order. The analogy with invertible sheaves can be pursued further. The analogue of the exact sequence
$$ 0 \rightarrow \mathbf Z \rightarrow {\mathcal O} _ {B} \mathop \rightarrow \limits ^ {\mathop {\rm exp}} {\mathcal O} _ {B} ^ {*} \rightarrow 1 $$
is the exact sequence
$$ 0 \rightarrow R ^ {1} \tau _ {0} \mathbf Z \rightarrow {\mathcal H} ^ {0} ( T ( {\mathcal J} ) / B ) \rightarrow {\mathcal H} ^ {0} ( {\mathcal J} / B ) \rightarrow 0 , $$
where $ {\mathcal H} ^ {0} ( T ( {\mathcal J} ) / B ) $ is the sheaf of local sections of the bundle $ T ( {\mathcal J} )/ B $ and $ T ( {\mathcal J} ) $ is the tangent space to the fibre $ \tau ^ {- 1 }( b) $ at $ e ( b) $. The boundary homomorphism
$$ \delta : H ^ {1} ( B , {\mathcal H} ^ {0} ( {\mathcal J} / B ) ) \rightarrow H ^ {2} ( B , R ^ {1} \tau _ {*} \mathbf Z ) $$
allows one to recognize when one fibration is a deformation of another. For that it is necessary and sufficient that the elements corresponding to these fibrations have one and the same image under $ \delta $ (see ).
The classification of algebraic elliptic surfaces.
Suppose that $ \mathop{\rm char} k = 0 $. For an elliptic surface $ X $ the canonical dimension $ k ( X) \leq 1 $, that is, it is equal to $ - 1 $, 0 or $ 1 $. If $ k ( X) = 1 $, $ X $ is said to be an elliptic surface of general type. These are characterized by the conditions $ 12 K _ {X} \neq 0 $ and $ | 12 K _ {X} | \neq \emptyset $. Elliptic surfaces with $ p _ {g} \geq 2 $ or, more generally, with $ P _ {m} \geq 2 $ for some $ m $, are of general type.
Elliptic surfaces with $ k ( X) = 0 $ are characterized by the condition $ 12 K _ {X} = 0 $. In this case $ \chi ( {\mathcal O} _ {X} ) $ can take the three values 2, 1 or $ 0 $. If $ \chi ( {\mathcal O} _ {X} )= 2 $, then $ X $ is an elliptic $ K 3 $-surface ( $ q = 0 $, $ K _ {X} = 0 $). In this case $ B $ is isomorphic to the projective line $ P ^ {1} $, the fibration has no multiple fibres and $ X $ has the invariants $ p _ {g} = 1 $, $ q = 0 $, $ b _ {2} = 22 $. If $ \chi ( {\mathcal O} _ {X} ) = 1 $, then $ X $ is an Enriques surface, that is, a surface with $ p _ {g} = q = 0 $, $ 2 K _ {X} = 0 $. (Every Enriques surface is elliptic.) In this case $ B \simeq P ^ {1} $, the fibration has two fibres of multiplicity 2, and $ X $ has the invariants $ p _ {g} = q = 0 $, $ b _ {2} = 10 $. If $ \chi ( {\mathcal O} _ {X} ) = 0 $, then two cases are possible. Either $ X $ is an Abelian variety (and then $ p _ {g} = 1 $, $ q = 2 $, $ b _ {2} = 6 $); or $ X $ is a hyper-elliptic surface, that is, a surface that has a finite unramified covering — the product of two elliptic curves. In that case $ p _ {g} = 0 $, $ b _ {1} = 2 $, $ b _ {2} = 2 $, $ B = P ^ {1} $, and $ \pi $ has 3 or 4 multiple fibres with four possibilities for their multiplicity: $ ( 3 , 3 , 3 ) $, $ ( 2 , 4 , 4 ) $, $ ( 2 , 3 , 6 ) $, and $ ( 2 , 2 , 2 , 2 ) $, and $ 3 K _ {X} = 0 $, $ 4 K _ {X} = 0 $, $ 6 K _ {X} = 0 $, and $ 2 K _ {X} = 0 $, respectively.
An elliptic surface with $ k ( X) = - 1 $ is ruled (cf. Ruled surface). It is characterized by the condition $ | 12 K _ {X} | = \emptyset $. Here two cases are possible: 1) $ X $ is a surface with $ p _ {g} = q = 0 $, $ b _ {2} = 10 $, and $ \pi $ has no multiple fibres or one; moreover, a surface without multiple fibres can be obtained as follows: one has to take a rational mapping $ P ^ {2} \rightarrow P ^ {1} $ determined by two cubics $ F _ {0} $ and $ F _ {1} $ and blow up their 9 points of intersection; or 2) $ X $ is a surface with $ p _ {g} = 0 $, $ q = 1 $, $ b _ {2} = 2 $, and the multiplicities $ m _ {i} $ are subject to the inequality
$$ \sum \left ( 1 - \frac{1}{m _ {i} } \right ) < 2 . $$
The formula for the canonical class and the classification of elliptic surfaces can also be generalized to the case of a field of finite characteristic [5], [6].
The classification of non-algebraic elliptic surfaces.
The classification of non-algebraic elliptic surfaces. For non-algebraic surfaces the algebraic dimension $ a ( X) = \mathop{\rm tr} \mathop{\rm deg} M ( X) $ is 1 or 0. If $ a ( X) = 0 $, then $ X $ is non-elliptic. All surfaces with $ a ( X) = 1 $ are elliptic. Here the structure of $ \pi : X \rightarrow B $ is determined almost canonically: Every such fibration $ \pi $ is necessarily elliptic. The classification by the canonical dimension is precisely the same as for algebraic elliptic surfaces: $ k ( X) = - 1 $ $ \iff $ $ | 12 K _ {X} | = \emptyset $; $ k ( X) = 0 $ $ \iff $ $ 12K _ {X} = 0 $; and $ k ( X) = 1 $ ($ X $ is of basic type) $ \iff $ $ | 12 K _ {X} | = \emptyset $, $ 12 K _ {X} \neq 0 $.
Non-algebraic elliptic surfaces with $ k ( X) = 0 $ belong to one of the following classes: 1) the $ K 3 $-surfaces ( $ \chi ( {\mathcal O} _ {X} )= 2 $, $ b _ {1} = 0 $, $ b _ {2} = 22 $, $ X $ is simply connected); 2) the complex tori ( $ K _ {X} = 0 $, $ \chi ( {\mathcal O} _ {X} ) = 0 $, $ b _ {1} = 4 $, $ b _ {2} = 6 $); 3) the Kodaira surfaces ( $ K _ {X} = 0 $, $ \chi ( {\mathcal O} _ {X} ) = 0 $, $ b _ {1} = 3 $, $ b _ {2} = 4 $). Primary Kodaira surfaces are holomorphically locally trivial fibrations over an elliptic curve with an elliptic curve as typical fibre, and from the point of view of differentiability, bundles over a $ 3 $-dimensional torus with a circle as fibre; or 4) the surfaces with $ \chi ( {\mathcal O} _ {X} ) = 0 $, $ p _ {g} = 0 $, $ b _ {1} = 1 $, $ b _ {2} = 0 $. For them $ m K _ {X} = 0 $ with $ m = 2 , 3 , 4 $, (analogous to hyper-elliptic surfaces). They have Kodaira surfaces as finite unramified coverings. In the cases 2), 3) and 4) $ \mathbf C ^ {2} $ is the universal covering of $ X $.
Non-algebraic elliptic surfaces with $ k ( X) = - 1 $ are Hopf surfaces, that is, their universal covering is $ \mathbf C ^ {2} \setminus 0 $. For them $ \chi ( {\mathcal O} _ {X} ) = 0 $, $ b _ {1} = 1 $, $ b _ {2} = 0 $. The proper Hopf surfaces are $ ( \mathbf C ^ {2} \setminus 0 ) / T $, where $ T ( z _ {1} , z _ {2} ) = ( \alpha _ {1} z _ {1} , \alpha _ {2} z _ {2} ) $ are real generators of $ T $. They are homeomorphic to $ S ^ {1} \times S ^ {2} $ and are characterized by this property. Arbitrary elliptic Hopf surfaces are quotients of proper Hopf surfaces .
References
| [1] | "Algebraic surfaces" Proc. Steklov Inst. Math. , 75 (1967) Trudy Mat. Inst. Steklov. , 75 (1965) Zbl 0172.37901 Zbl 0153.22401 |
| [2] | D. Husemoller, "Classification and embeddings of surfaces" R. Hartshorne (ed.) , Algebraic geometry (Arcata, 1974) , Proc. Symp. Pure Math. , 29 , Amer. Math. Soc. (1982) pp. 329–420 MR0506292 Zbl 0326.14009 |
| [3a] | K. Kodaira, "On compact complex analytic surfaces I" Ann. of Math. (2) , 71 (10) pp. 111–152 MR0132556 Zbl 0137.17501 Zbl 0098.13004 |
| [3b] | K. Kodaira, "On compact complex analytic surfaces II" Ann. of Math. (2) , 77 (1963) pp. 563–626 MR165541 Zbl 0193.37701 Zbl 0133.16505 |
| [3c] | K. Kodaira, "On compact complex analytic surfaces III" Ann. of Math. (2) , 78 (1963) pp. 1–40 MR165541 Zbl 0193.37701 |
| [4a] | K. Kodaira, "On the structure of compact complex analytic surfaces I" Amer. J. Math. , 86 (1964) pp. 751–798 MR0187255 Zbl 0137.17501 |
| [4b] | K. Kodaira, "On the structure of compact complex analytic surfaces II" Amer. J. Math. , 88 (1966) pp. 682–721 MR0205280 Zbl 0193.37701 |
| [4c] | K. Kodaira, "On the structure of compact complex analytic surfaces III" Amer. J. Math. , 90 (1968) pp. 55–83 MR0228019 Zbl 0193.37701 |
| [4d] | K. Kodaira, "On the structure of compact complex analytic surfaces IV" Amer. J. Math. , 90 (1968) pp. 1048–1066 MR239114 |
| [5] | D. Mumford, "Enriques' classification of surfaces in char 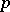 . I" D.C. Spencer (ed.) S. Iyanaga (ed.) , Global analysis (papers in honor of K. Kodaira) , Princeton Univ. Press (1969) pp. 325–339 MR0491719 MR0491720 . I" D.C. Spencer (ed.) S. Iyanaga (ed.) , Global analysis (papers in honor of K. Kodaira) , Princeton Univ. Press (1969) pp. 325–339 MR0491719 MR0491720 |
| [6] | E. Bombieri, D. Mumford, "Enriques' classification of surfaces in char 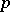 . II" W.L. Baily jr. (ed.) T. Shioda (ed.) , Complex Analysis and Algebraic geometry , Cambridge Univ. Press & Iwanami Shoten (1977) pp. 23–42 MR0491719 MR0491720 . II" W.L. Baily jr. (ed.) T. Shioda (ed.) , Complex Analysis and Algebraic geometry , Cambridge Univ. Press & Iwanami Shoten (1977) pp. 23–42 MR0491719 MR0491720 |
Comments
A secondary Kodaira surface is a surface other than a primary one, admitting a primary Kodaira surface as an unramified covering. They are elliptic fibrations over a rational curve. Their first Betti number is 1.
The canonical dimension $ k ( X) $ mentioned at the start of the section on classification of algebraic elliptic surfaces is the Kodaira dimension $ \mathop{\rm Kod} ( X) $ (with $ k ( X) = - 1 $ if $ \mathop{\rm Kod} ( X) = - \infty $).
References
| [a1] | W. Barth, C. Peters, A. van der Ven, "Compact complex surfaces" , Springer (1984) MR0749574 Zbl 0718.14023 |
Elliptic surface. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Elliptic_surface&oldid=23821