Difference between revisions of "Monoidal transformation"
(Category:Algebraic geometry) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | m0647502.png | ||
| + | $#A+1 = 45 n = 3 | ||
| + | $#C+1 = 45 : ~/encyclopedia/old_files/data/M064/M.0604750 Monoidal transformation, | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | ''blowing up, $ \sigma $- | |
| + | process'' | ||
| − | + | A special kind of [[Birational morphism|birational morphism]] of an algebraic variety or bimeromorphic morphism of an analytic space. For example, let $ X $ | |
| + | be an algebraic variety (or an arbitrary scheme), and let $ D \subset X $ | ||
| + | be a closed subvariety given by a sheaf of ideals $ J $. | ||
| + | The monoidal transformation of $ X $ | ||
| + | with centre $ D $ | ||
| + | is the $ X $- | ||
| + | scheme $ X ^ {1} = \mathop{\rm Proj} ( \oplus _ {n \geq 0 } J ^ {n)} $— | ||
| + | the projective spectrum of the graded sheaf of $ {\mathcal O} _ {X} $- | ||
| + | algebras $ \oplus _ {n \geq 0 } J ^ {n} $. | ||
| + | If $ f : X ^ {1} \rightarrow X $ | ||
| + | is the structure morphism of the $ X $- | ||
| + | scheme $ X ^ {1} $, | ||
| + | then the sheaf of ideals $ f ^ { * } ( J) = J \cdot {\mathcal O} _ {X ^ {1} } $ | ||
| + | on $ X ^ {1} $( | ||
| + | defining the exceptional subscheme $ f ^ { - 1 } ( D ) $ | ||
| + | on $ X ^ {1} $) | ||
| + | is invertible. This means that $ f ^ { - 1 } ( D ) $ | ||
| + | is a [[Divisor|divisor]] on $ X ^ {1} $; | ||
| + | in addition, $ f $ | ||
| + | induces an isomorphism between $ X ^ {1} \setminus f ^ { - 1 } ( D ) $ | ||
| + | and $ X \setminus D $. | ||
| + | A monoidal transformation $ f : X ^ {1} \rightarrow X $ | ||
| + | of a scheme $ X $ | ||
| + | with centre $ D $ | ||
| + | is characterized by the following universal property [[#References|[1]]]: The sheaf of ideals $ f ^ { * } ( J ) $ | ||
| + | is invertible and for any morphism $ g : X _ {1} \rightarrow X $ | ||
| + | for which $ g ^ {*} ( J ) $ | ||
| + | is invertible there is a unique morphism $ h : X _ {1} \rightarrow X ^ {1} $ | ||
| + | such that $ g = f \circ h $. | ||
| − | Admissible monoidal transformations of non-singular varieties are particularly simple to construct. If | + | A monoidal transformation of an algebraic or analytic space $ X $ |
| + | with as centre a closed subspace $ D \subset X $ | ||
| + | can be defined and characterized in the same way. | ||
| + | |||
| + | An important class of monoidal transformations are the admissible monoidal transformations, which are distinguished by the condition that $ D $ | ||
| + | is non-singular and $ X $ | ||
| + | is a normally flat scheme along $ D $. | ||
| + | The latter means that all sheaves $ J ^ {n} / J ^ {n+} 1 $ | ||
| + | are flat $ ( {\mathcal O} _ {X} / J ) $- | ||
| + | modules. The importance of admissible monoidal transformations is explained by the fact that they do not worsen the singularities of the variety. In addition, it has been proved (see [[#References|[1]]]) that a suitable sequence of admissible monoidal transformations improves singularities, which allows one to prove the theorem on the resolution of singularities for an algebraic variety over a field of characteristic zero. | ||
| + | |||
| + | Admissible monoidal transformations of non-singular varieties are particularly simple to construct. If $ f : X _ {1} \rightarrow X $ | ||
| + | is a monoidal transformation with a non-singular centre $ D \subset X $, | ||
| + | then $ X _ {1} $ | ||
| + | is again non-singular and the exceptional subspace $ f ^ { - 1 } ( D ) $ | ||
| + | is canonically isomorphic to the projectivization of the conormal sheaf to $ D $ | ||
| + | in $ X $. | ||
| + | In the special case when $ D $ | ||
| + | consists of one point, the monoidal transformation consists of blowing up this point into the whole projective space of tangent directions. For the behaviour of various invariants of non-singular varieties (such as Chow rings, cohomology spaces, the $ K $- | ||
| + | functor, and Chern classes) under admissible monoidal transformations see [[#References|[2]]]–[[#References|[5]]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> H. Hironaka, "Resolution of an algebraic variety over a field of characteristic zero I, II" ''Ann. of Math. (2)'' , '''79''' (1964) pp. 109–326 {{MR|199184}} {{ZBL|0122.38603}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> P. Berthelot (ed.) A. Grothendieck (ed.) L. Illusie (ed.) et al. (ed.) , ''Théorie des intersections et théorème de Riemann–Roch (SGA 6)'' , ''Lect. notes in math.'' , '''225''' , Springer (1971)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> A. Grothendieck, I. Bucur, C. Honzel, L. Illusie, J.-P. Jouanolou, J.-P. Serre, "Cohomologie <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064750/m06475047.png" />-adique et fonctions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064750/m06475048.png" />. SGA 5" , ''Lect. notes in math.'' , '''589''' , Springer (1977) {{MR|491704}} {{ZBL|}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> I. Porteous, "Blowing up Chern classes" ''Proc. Cambridge Philos. Soc.'' , '''56''' : 2 (1960) pp. 118–124 {{MR|0121813}} {{ZBL|0166.16701}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> Yu.I. Manin, "Lectures on the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064750/m06475049.png" />-functor in algebraic geometry" ''Russian Math. Surveys'' , '''24''' (1969) pp. 1–89 ''Uspekhi Mat. Nauk'' , '''24''' : 5 (1969) pp. 3–86 {{MR|265355}} {{ZBL|}} </TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> H. Hironaka, "Resolution of an algebraic variety over a field of characteristic zero I, II" ''Ann. of Math. (2)'' , '''79''' (1964) pp. 109–326 {{MR|199184}} {{ZBL|0122.38603}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> P. Berthelot (ed.) A. Grothendieck (ed.) L. Illusie (ed.) et al. (ed.) , ''Théorie des intersections et théorème de Riemann–Roch (SGA 6)'' , ''Lect. notes in math.'' , '''225''' , Springer (1971)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> A. Grothendieck, I. Bucur, C. Honzel, L. Illusie, J.-P. Jouanolou, J.-P. Serre, "Cohomologie <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064750/m06475047.png" />-adique et fonctions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064750/m06475048.png" />. SGA 5" , ''Lect. notes in math.'' , '''589''' , Springer (1977) {{MR|491704}} {{ZBL|}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> I. Porteous, "Blowing up Chern classes" ''Proc. Cambridge Philos. Soc.'' , '''56''' : 2 (1960) pp. 118–124 {{MR|0121813}} {{ZBL|0166.16701}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> Yu.I. Manin, "Lectures on the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064750/m06475049.png" />-functor in algebraic geometry" ''Russian Math. Surveys'' , '''24''' (1969) pp. 1–89 ''Uspekhi Mat. Nauk'' , '''24''' : 5 (1969) pp. 3–86 {{MR|265355}} {{ZBL|}} </TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
Revision as of 08:01, 6 June 2020
blowing up, $ \sigma $-
process
A special kind of birational morphism of an algebraic variety or bimeromorphic morphism of an analytic space. For example, let $ X $ be an algebraic variety (or an arbitrary scheme), and let $ D \subset X $ be a closed subvariety given by a sheaf of ideals $ J $. The monoidal transformation of $ X $ with centre $ D $ is the $ X $- scheme $ X ^ {1} = \mathop{\rm Proj} ( \oplus _ {n \geq 0 } J ^ {n)} $— the projective spectrum of the graded sheaf of $ {\mathcal O} _ {X} $- algebras $ \oplus _ {n \geq 0 } J ^ {n} $. If $ f : X ^ {1} \rightarrow X $ is the structure morphism of the $ X $- scheme $ X ^ {1} $, then the sheaf of ideals $ f ^ { * } ( J) = J \cdot {\mathcal O} _ {X ^ {1} } $ on $ X ^ {1} $( defining the exceptional subscheme $ f ^ { - 1 } ( D ) $ on $ X ^ {1} $) is invertible. This means that $ f ^ { - 1 } ( D ) $ is a divisor on $ X ^ {1} $; in addition, $ f $ induces an isomorphism between $ X ^ {1} \setminus f ^ { - 1 } ( D ) $ and $ X \setminus D $. A monoidal transformation $ f : X ^ {1} \rightarrow X $ of a scheme $ X $ with centre $ D $ is characterized by the following universal property [1]: The sheaf of ideals $ f ^ { * } ( J ) $ is invertible and for any morphism $ g : X _ {1} \rightarrow X $ for which $ g ^ {*} ( J ) $ is invertible there is a unique morphism $ h : X _ {1} \rightarrow X ^ {1} $ such that $ g = f \circ h $.
A monoidal transformation of an algebraic or analytic space $ X $ with as centre a closed subspace $ D \subset X $ can be defined and characterized in the same way.
An important class of monoidal transformations are the admissible monoidal transformations, which are distinguished by the condition that $ D $ is non-singular and $ X $ is a normally flat scheme along $ D $. The latter means that all sheaves $ J ^ {n} / J ^ {n+} 1 $ are flat $ ( {\mathcal O} _ {X} / J ) $- modules. The importance of admissible monoidal transformations is explained by the fact that they do not worsen the singularities of the variety. In addition, it has been proved (see [1]) that a suitable sequence of admissible monoidal transformations improves singularities, which allows one to prove the theorem on the resolution of singularities for an algebraic variety over a field of characteristic zero.
Admissible monoidal transformations of non-singular varieties are particularly simple to construct. If $ f : X _ {1} \rightarrow X $ is a monoidal transformation with a non-singular centre $ D \subset X $, then $ X _ {1} $ is again non-singular and the exceptional subspace $ f ^ { - 1 } ( D ) $ is canonically isomorphic to the projectivization of the conormal sheaf to $ D $ in $ X $. In the special case when $ D $ consists of one point, the monoidal transformation consists of blowing up this point into the whole projective space of tangent directions. For the behaviour of various invariants of non-singular varieties (such as Chow rings, cohomology spaces, the $ K $- functor, and Chern classes) under admissible monoidal transformations see [2]–[5].
References
| [1] | H. Hironaka, "Resolution of an algebraic variety over a field of characteristic zero I, II" Ann. of Math. (2) , 79 (1964) pp. 109–326 MR199184 Zbl 0122.38603 |
| [2] | P. Berthelot (ed.) A. Grothendieck (ed.) L. Illusie (ed.) et al. (ed.) , Théorie des intersections et théorème de Riemann–Roch (SGA 6) , Lect. notes in math. , 225 , Springer (1971) |
| [3] | A. Grothendieck, I. Bucur, C. Honzel, L. Illusie, J.-P. Jouanolou, J.-P. Serre, "Cohomologie 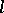 -adique et fonctions -adique et fonctions 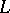 . SGA 5" , Lect. notes in math. , 589 , Springer (1977) MR491704 . SGA 5" , Lect. notes in math. , 589 , Springer (1977) MR491704 |
| [4] | I. Porteous, "Blowing up Chern classes" Proc. Cambridge Philos. Soc. , 56 : 2 (1960) pp. 118–124 MR0121813 Zbl 0166.16701 |
| [5] | Yu.I. Manin, "Lectures on the 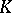 -functor in algebraic geometry" Russian Math. Surveys , 24 (1969) pp. 1–89 Uspekhi Mat. Nauk , 24 : 5 (1969) pp. 3–86 MR265355 -functor in algebraic geometry" Russian Math. Surveys , 24 (1969) pp. 1–89 Uspekhi Mat. Nauk , 24 : 5 (1969) pp. 3–86 MR265355 |
Comments
The word "s-process" appeared for the first time in [a1].
References
| [a1] | H. Hopf, "Schlichte Abbildungen und lokale Modifikationen 4-dimensionaler komplexer Mannigfaltigkeiten" Comm. Math. Helv. , 29 (1954) pp. 132–156 MR0068008 Zbl 0064.41703 |
Monoidal transformation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Monoidal_transformation&oldid=34206