Difference between revisions of "Conic sections"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | c0249601.png | ||
| + | $#A+1 = 24 n = 0 | ||
| + | $#C+1 = 24 : ~/encyclopedia/old_files/data/C024/C.0204960 Conic sections | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
Curves obtained by intersecting a right circular cone by planes not passing through its vertex. A conic section can be of one of three types: 1) the intersecting plane can meet all generators of the cone and does so only in points of one and the same convex half-cone (Fig.a); the curve of intersection is a closed oval — an [[Ellipse|ellipse]]; a circle is obtained as a special case of the ellipse when the intersecting plane is perpendicular to the axis of the cone. 2) The intersecting plane is parallel to one of the tangent planes to the cone (Fig.b); the intersection is a non-closed curve going off to infinity — a [[Parabola|parabola]], entirely located in one half-cone. 3) The intersecting plane meets both half-cones (Fig.c); the intersection is a [[Hyperbola|hyperbola]] — it consists of two congruent non-closed parts that go off to infinity (the branches (sheets) of the hyperbola), each located in one of the two half-cones. | Curves obtained by intersecting a right circular cone by planes not passing through its vertex. A conic section can be of one of three types: 1) the intersecting plane can meet all generators of the cone and does so only in points of one and the same convex half-cone (Fig.a); the curve of intersection is a closed oval — an [[Ellipse|ellipse]]; a circle is obtained as a special case of the ellipse when the intersecting plane is perpendicular to the axis of the cone. 2) The intersecting plane is parallel to one of the tangent planes to the cone (Fig.b); the intersection is a non-closed curve going off to infinity — a [[Parabola|parabola]], entirely located in one half-cone. 3) The intersecting plane meets both half-cones (Fig.c); the intersection is a [[Hyperbola|hyperbola]] — it consists of two congruent non-closed parts that go off to infinity (the branches (sheets) of the hyperbola), each located in one of the two half-cones. | ||
| Line 17: | Line 29: | ||
In the cases where the conic section has a centre of symmetry (the centre), that is, in the case of an ellipse or a hyperbola, its equation can be reduced (by moving the coordinate origin to the centre) to the form: | In the cases where the conic section has a centre of symmetry (the centre), that is, in the case of an ellipse or a hyperbola, its equation can be reduced (by moving the coordinate origin to the centre) to the form: | ||
| − | + | $$ | |
| + | a _ {11} x ^ {2} + 2a _ {12} xy + a _ {22} y ^ {2} = a _ {33} . | ||
| + | $$ | ||
Further investigation of such conic sections (the so-called central conic sections) shows that their equations can be reduced to a still simpler form: | Further investigation of such conic sections (the so-called central conic sections) shows that their equations can be reduced to a still simpler form: | ||
| − | + | $$ \tag{* } | |
| + | Ax ^ {2} + By ^ {2} = C, | ||
| + | $$ | ||
| − | by choosing the directions of the coordinate axes along the so-called principal axes (axes of symmetry) of the conic section. If | + | by choosing the directions of the coordinate axes along the so-called principal axes (axes of symmetry) of the conic section. If $ A $ |
| + | and $ B $ | ||
| + | have the same sign (as that of $ C $), | ||
| + | equation (*) defines an ellipse; if $ A $ | ||
| + | and $ B $ | ||
| + | have opposite signs, it defines a hyperbola. | ||
The equation of a parabola cannot be reduced to the form (*). With an appropriate choice of coordinate axes (such that one of them is the unique axis of symmetry of the parabola, the other the line perpendicular to it passing through the vertex of the parabola) the equation can be brought into the form | The equation of a parabola cannot be reduced to the form (*). With an appropriate choice of coordinate axes (such that one of them is the unique axis of symmetry of the parabola, the other the line perpendicular to it passing through the vertex of the parabola) the equation can be brought into the form | ||
| − | + | $$ | |
| + | y ^ {2} = 2px. | ||
| + | $$ | ||
The conic sections were known already to the mathematicians of Ancient Greece. The most complete work concerned with these curves at that time was the book Conic Sections of Apollonius of Perga (circa 200 B.C.). Later achievements in the theory of conic sections were connected with the invention of new geometrical methods in the 17th century: the projective method (G. Desargues, B. Pascal), and especially the coordinate method (R. Descartes, P. Fermat). | The conic sections were known already to the mathematicians of Ancient Greece. The most complete work concerned with these curves at that time was the book Conic Sections of Apollonius of Perga (circa 200 B.C.). Later achievements in the theory of conic sections were connected with the invention of new geometrical methods in the 17th century: the projective method (G. Desargues, B. Pascal), and especially the coordinate method (R. Descartes, P. Fermat). | ||
| Line 33: | Line 56: | ||
Using another appropriate choice of the coordinate system (the axis of symmetry of the conic section as abscissa and the tangent at a vertex as ordinate), the equation of a conic section can be reduced to the form | Using another appropriate choice of the coordinate system (the axis of symmetry of the conic section as abscissa and the tangent at a vertex as ordinate), the equation of a conic section can be reduced to the form | ||
| − | + | $$ | |
| + | y ^ {2} = \ | ||
| + | 2px + \lambda x ^ {2} | ||
| + | $$ | ||
| − | (here | + | (here $ p $ |
| + | and $ \lambda $ | ||
| + | are constants). If $ p \neq 0 $, | ||
| + | it defines a parabola when $ \lambda = 0 $, | ||
| + | an ellipse when $ \lambda < 0 $, | ||
| + | and a hyperbola when $ \lambda > 0 $. | ||
| + | The geometrical properties of a conic section given by this equation were known to the ancient geometers, and served for Apollonius of Perga as the reason for giving the various types of conic sections their names. These names have survived to the present day: the word "parabola" ( $ \pi \alpha \rho \alpha \beta \omikron \lambda \eta $ | ||
| + | in Greek) means "application" (because in Greek geometry the transformation of a rectangle of given area $ y ^ {2} $ | ||
| + | into a rectangle of equal area with given base $ 2p $ | ||
| + | was called the application of the given rectangle to the base); the word "ellipse" ( $ \epsilon \lambda \lambda \epsilon \iota \psi \iota \sigma $ | ||
| + | in Greek) means "deficiency" (application with deficiency); "hyperbola" ( $ \upsilon \pi \epsilon \rho \beta \omikron \lambda \eta $ | ||
| + | in Greek) means "excess" (application with excess). | ||
| − | With the transition to modern methods of investigation, the stereogeometrical definition of conic sections was replaced by planimetrical definitions of them as sets of points in the plane. E.g. an ellipse is defined as the set of points the sum of whose distances from two given points (the foci) has a given value. Another planimetrical definition of conic sections can be given, encompassing all three types of these curves: A conic section is the set of points such that the ratio of their distances to a given point (the focus) and to a given line (the directrix) is a fixed positive number | + | With the transition to modern methods of investigation, the stereogeometrical definition of conic sections was replaced by planimetrical definitions of them as sets of points in the plane. E.g. an ellipse is defined as the set of points the sum of whose distances from two given points (the foci) has a given value. Another planimetrical definition of conic sections can be given, encompassing all three types of these curves: A conic section is the set of points such that the ratio of their distances to a given point (the focus) and to a given line (the directrix) is a fixed positive number $ e $( |
| + | the eccentricity). If $ e < 1 $, | ||
| + | the conic section is an ellipse; if $ e > 1 $, | ||
| + | it is a hyperbola; if $ e = 1 $ | ||
| + | it is a parabola. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> P.S. Aleksandrov, "Lectures on analytical geometry" , Moscow (1968) (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> B.L. van der Waerden, "Ontwakende wetenschap" , Noordhoff (1957)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> P.S. Aleksandrov, "Lectures on analytical geometry" , Moscow (1968) (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> B.L. van der Waerden, "Ontwakende wetenschap" , Noordhoff (1957)</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
Revision as of 17:46, 4 June 2020
Curves obtained by intersecting a right circular cone by planes not passing through its vertex. A conic section can be of one of three types: 1) the intersecting plane can meet all generators of the cone and does so only in points of one and the same convex half-cone (Fig.a); the curve of intersection is a closed oval — an ellipse; a circle is obtained as a special case of the ellipse when the intersecting plane is perpendicular to the axis of the cone. 2) The intersecting plane is parallel to one of the tangent planes to the cone (Fig.b); the intersection is a non-closed curve going off to infinity — a parabola, entirely located in one half-cone. 3) The intersecting plane meets both half-cones (Fig.c); the intersection is a hyperbola — it consists of two congruent non-closed parts that go off to infinity (the branches (sheets) of the hyperbola), each located in one of the two half-cones.
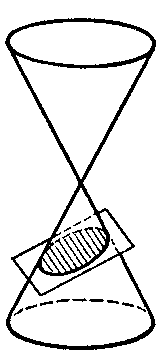
Figure: c024960a
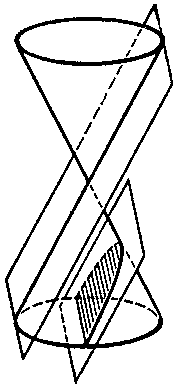
Figure: c024960b

Figure: c024960c
From the point of view of analytic geometry, a conic section is a real non-degenerate second-order curve.
In the cases where the conic section has a centre of symmetry (the centre), that is, in the case of an ellipse or a hyperbola, its equation can be reduced (by moving the coordinate origin to the centre) to the form:
$$ a _ {11} x ^ {2} + 2a _ {12} xy + a _ {22} y ^ {2} = a _ {33} . $$
Further investigation of such conic sections (the so-called central conic sections) shows that their equations can be reduced to a still simpler form:
$$ \tag{* } Ax ^ {2} + By ^ {2} = C, $$
by choosing the directions of the coordinate axes along the so-called principal axes (axes of symmetry) of the conic section. If $ A $ and $ B $ have the same sign (as that of $ C $), equation (*) defines an ellipse; if $ A $ and $ B $ have opposite signs, it defines a hyperbola.
The equation of a parabola cannot be reduced to the form (*). With an appropriate choice of coordinate axes (such that one of them is the unique axis of symmetry of the parabola, the other the line perpendicular to it passing through the vertex of the parabola) the equation can be brought into the form
$$ y ^ {2} = 2px. $$
The conic sections were known already to the mathematicians of Ancient Greece. The most complete work concerned with these curves at that time was the book Conic Sections of Apollonius of Perga (circa 200 B.C.). Later achievements in the theory of conic sections were connected with the invention of new geometrical methods in the 17th century: the projective method (G. Desargues, B. Pascal), and especially the coordinate method (R. Descartes, P. Fermat).
Using another appropriate choice of the coordinate system (the axis of symmetry of the conic section as abscissa and the tangent at a vertex as ordinate), the equation of a conic section can be reduced to the form
$$ y ^ {2} = \ 2px + \lambda x ^ {2} $$
(here $ p $ and $ \lambda $ are constants). If $ p \neq 0 $, it defines a parabola when $ \lambda = 0 $, an ellipse when $ \lambda < 0 $, and a hyperbola when $ \lambda > 0 $. The geometrical properties of a conic section given by this equation were known to the ancient geometers, and served for Apollonius of Perga as the reason for giving the various types of conic sections their names. These names have survived to the present day: the word "parabola" ( $ \pi \alpha \rho \alpha \beta \omikron \lambda \eta $ in Greek) means "application" (because in Greek geometry the transformation of a rectangle of given area $ y ^ {2} $ into a rectangle of equal area with given base $ 2p $ was called the application of the given rectangle to the base); the word "ellipse" ( $ \epsilon \lambda \lambda \epsilon \iota \psi \iota \sigma $ in Greek) means "deficiency" (application with deficiency); "hyperbola" ( $ \upsilon \pi \epsilon \rho \beta \omikron \lambda \eta $ in Greek) means "excess" (application with excess).
With the transition to modern methods of investigation, the stereogeometrical definition of conic sections was replaced by planimetrical definitions of them as sets of points in the plane. E.g. an ellipse is defined as the set of points the sum of whose distances from two given points (the foci) has a given value. Another planimetrical definition of conic sections can be given, encompassing all three types of these curves: A conic section is the set of points such that the ratio of their distances to a given point (the focus) and to a given line (the directrix) is a fixed positive number $ e $( the eccentricity). If $ e < 1 $, the conic section is an ellipse; if $ e > 1 $, it is a hyperbola; if $ e = 1 $ it is a parabola.
References
| [1] | P.S. Aleksandrov, "Lectures on analytical geometry" , Moscow (1968) (In Russian) |
| [2] | B.L. van der Waerden, "Ontwakende wetenschap" , Noordhoff (1957) |
Comments
All conic sections are projectively equivalent (cf. Projective transformation). A conic section is an ellipse, a parabola or a hyperbola, respectively, if and only if its intersection with the line at infinity (cf. Projective plane) consists of 0, 1 or 2 points, respectively.
References
| [a1] | H.S.M. Coxeter, "Projective geometry" , Univ. Toronto Press (1974) |
Conic sections. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Conic_sections&oldid=14628