Difference between revisions of "One-sided and two-sided surfaces"
(Importing text file) |
(TeX) |
||
| Line 1: | Line 1: | ||
| − | Two types of surfaces, differing in the way in which they are situated in the ambient space (one-sided position and two-sided position). For example, the cylinder is a two-sided surface, while the [[Möbius strip|Möbius strip]] is a one-sided surface. A characteristic distinction between these surfaces is that the boundary of the cylinder consists of two curves, while the boundary of the Möbius strip is a single curve. Among the closed surfaces the [[Sphere|sphere]] and the [[Torus|torus]] are two-sided, while the [[Klein surface|Klein surface]] is one-sided. As examples of two-sided and one-sided situations one may cite imbeddings of the circle in the Möbius strip. Thus, the cycle | + | {{TEX|done}} |
| + | Two types of surfaces, differing in the way in which they are situated in the ambient space (one-sided position and two-sided position). For example, the cylinder is a two-sided surface, while the [[Möbius strip|Möbius strip]] is a one-sided surface. A characteristic distinction between these surfaces is that the boundary of the cylinder consists of two curves, while the boundary of the Möbius strip is a single curve. Among the closed surfaces the [[Sphere|sphere]] and the [[Torus|torus]] are two-sided, while the [[Klein surface|Klein surface]] is one-sided. As examples of two-sided and one-sided situations one may cite imbeddings of the circle in the Möbius strip. Thus, the cycle $\alpha$ (see Fig.) is a one-sided curve, while the cycle $\beta$ is two-sided (in general, any [[Desorienting path|desorienting path]] lies in the surface one-sidedly). | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/o068230a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/o068230a.gif" /> | ||
| Line 5: | Line 6: | ||
Figure: o068230a | Figure: o068230a | ||
| − | More precisely, one- and two-sided surfaces are two types of manifolds differing in the way in which they are imbedded in the ambient space (of dimension higher by one). Two-sidedness and one-sidedness are related to orientability and non-orientability (see [[Orientation|Orientation]]), but unlike these, are not intrinsic properties of the surface and depend on the ambient space. For example, there exist orientable two-sided surfaces: | + | More precisely, one- and two-sided surfaces are two types of manifolds differing in the way in which they are imbedded in the ambient space (of dimension higher by one). Two-sidedness and one-sidedness are related to orientability and non-orientability (see [[Orientation|Orientation]]), but unlike these, are not intrinsic properties of the surface and depend on the ambient space. For example, there exist orientable two-sided surfaces: $S^2\subset S^3$, $T^2\subset\mathbf R^3$; non-orientable two-sided surfaces: $\mathbf RP^2\times0\subset\mathbf RP^2\times S^1$; orientable one-sided surfaces: $T^2=S^1\times S^1\subset\mathbf RP^2\times S^1$; non-orientable one-sided surfaces: $\mathbf RP^2\subset\mathbf RP^3$ (here $S^2$ is the sphere, $T^2$ the torus, $\mathbf RP^2$ the projective plane, $\mathbf RP^3$ projective space, and $S^1$ a desorienting path on $\mathbf RP^2$). |
| − | In an orientable space (e.g. in | + | In an orientable space (e.g. in $\mathbf R^n$) a hypersurface is orientable if and only if it is two-sided. |
| − | Suppose that a normal vector is moved along a closed curve on a smooth surface immersed in some space in such a way that it remains normal. If upon return to the starting point the direction of the normal is the same as it was originally, independently of the choice of curve, then the surface is called two-sided; in the opposite case it is called one-sided. More generally, a surface | + | Suppose that a normal vector is moved along a closed curve on a smooth surface immersed in some space in such a way that it remains normal. If upon return to the starting point the direction of the normal is the same as it was originally, independently of the choice of curve, then the surface is called two-sided; in the opposite case it is called one-sided. More generally, a surface $\Pi$ is situated two-sidedly if and only if its [[Normal bundle|normal bundle]] is trivial (there exists a non-zero section in this bundle). Conversely, the normal bundle of a one-sided surface is non-trivial: There exists a curve on $\Pi$ over which the bundle is a Möbius strip. |
| − | Locally every (hyper) surface | + | Locally every (hyper) surface $M^{n-1}$ in a space $N^n$ divides $N^n$ into two parts, that is, a point $x\in M^{n-1}\subset N^n$ has a neighbourhood $U\subset N$ such that $U$ consists of two components $U'$ and $U''$ and $U\cap M^{n-1}$ belongs to their common boundary. On the other hand, a sufficiently small neighbourhood of $M^{n-1}$ in $N^n$ (if $M$ is closed in $N$) has either one or two components the boundaries of which contain $M$. In the first case, the (hyper) surface $M^{n-1}$ is also called one-sided, and in the second case, two-sided. Thus, although the surface locally has two sides, globally it may be one-sided, while, in contrast, a two-sided surface need not divide its neighbourhood in the space. |
| − | For a two-sided surface | + | For a two-sided surface $M^n$ lying in $N^{n+1}$, the [[Intersection index (in homology)|intersection index (in homology)]] in $N^{n+1}$ of any closed curve $\alpha$ in $M^n$ satisfies the equation $(\alpha, M^n)\equiv0$ $\bmod\,2$. But if $M^n$ is one-sided, then $(\alpha,M^n)\neq0$ for some curve $\alpha\in M^n$. This fact can also be taken as the definition of one- and two-sidedness (along with the movement of a normal vector and the division of a neighbourhood). |
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> D. Hilbert, S.E. Cohn-Vossen, "Geometry and the imagination" , Chelsea (1952) (Translated from German)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> H. Seifert, W. Threlfall, "A textbook of topology" , Acad. Press (1980) (Translated from German)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> D.B. Fuks, A.T. Fomenko, V.L. Gutenmakher, "Homotopic topology" , Moscow (1969) (In Russian)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> D. Hilbert, S.E. Cohn-Vossen, "Geometry and the imagination" , Chelsea (1952) (Translated from German)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> H. Seifert, W. Threlfall, "A textbook of topology" , Acad. Press (1980) (Translated from German)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> D.B. Fuks, A.T. Fomenko, V.L. Gutenmakher, "Homotopic topology" , Moscow (1969) (In Russian)</TD></TR></table> | ||
Latest revision as of 16:10, 5 August 2014
Two types of surfaces, differing in the way in which they are situated in the ambient space (one-sided position and two-sided position). For example, the cylinder is a two-sided surface, while the Möbius strip is a one-sided surface. A characteristic distinction between these surfaces is that the boundary of the cylinder consists of two curves, while the boundary of the Möbius strip is a single curve. Among the closed surfaces the sphere and the torus are two-sided, while the Klein surface is one-sided. As examples of two-sided and one-sided situations one may cite imbeddings of the circle in the Möbius strip. Thus, the cycle $\alpha$ (see Fig.) is a one-sided curve, while the cycle $\beta$ is two-sided (in general, any desorienting path lies in the surface one-sidedly).
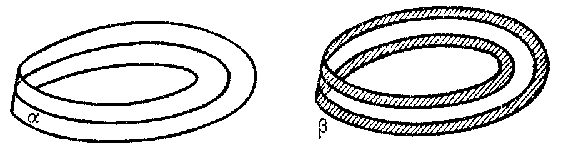
Figure: o068230a
More precisely, one- and two-sided surfaces are two types of manifolds differing in the way in which they are imbedded in the ambient space (of dimension higher by one). Two-sidedness and one-sidedness are related to orientability and non-orientability (see Orientation), but unlike these, are not intrinsic properties of the surface and depend on the ambient space. For example, there exist orientable two-sided surfaces: $S^2\subset S^3$, $T^2\subset\mathbf R^3$; non-orientable two-sided surfaces: $\mathbf RP^2\times0\subset\mathbf RP^2\times S^1$; orientable one-sided surfaces: $T^2=S^1\times S^1\subset\mathbf RP^2\times S^1$; non-orientable one-sided surfaces: $\mathbf RP^2\subset\mathbf RP^3$ (here $S^2$ is the sphere, $T^2$ the torus, $\mathbf RP^2$ the projective plane, $\mathbf RP^3$ projective space, and $S^1$ a desorienting path on $\mathbf RP^2$).
In an orientable space (e.g. in $\mathbf R^n$) a hypersurface is orientable if and only if it is two-sided.
Suppose that a normal vector is moved along a closed curve on a smooth surface immersed in some space in such a way that it remains normal. If upon return to the starting point the direction of the normal is the same as it was originally, independently of the choice of curve, then the surface is called two-sided; in the opposite case it is called one-sided. More generally, a surface $\Pi$ is situated two-sidedly if and only if its normal bundle is trivial (there exists a non-zero section in this bundle). Conversely, the normal bundle of a one-sided surface is non-trivial: There exists a curve on $\Pi$ over which the bundle is a Möbius strip.
Locally every (hyper) surface $M^{n-1}$ in a space $N^n$ divides $N^n$ into two parts, that is, a point $x\in M^{n-1}\subset N^n$ has a neighbourhood $U\subset N$ such that $U$ consists of two components $U'$ and $U''$ and $U\cap M^{n-1}$ belongs to their common boundary. On the other hand, a sufficiently small neighbourhood of $M^{n-1}$ in $N^n$ (if $M$ is closed in $N$) has either one or two components the boundaries of which contain $M$. In the first case, the (hyper) surface $M^{n-1}$ is also called one-sided, and in the second case, two-sided. Thus, although the surface locally has two sides, globally it may be one-sided, while, in contrast, a two-sided surface need not divide its neighbourhood in the space.
For a two-sided surface $M^n$ lying in $N^{n+1}$, the intersection index (in homology) in $N^{n+1}$ of any closed curve $\alpha$ in $M^n$ satisfies the equation $(\alpha, M^n)\equiv0$ $\bmod\,2$. But if $M^n$ is one-sided, then $(\alpha,M^n)\neq0$ for some curve $\alpha\in M^n$. This fact can also be taken as the definition of one- and two-sidedness (along with the movement of a normal vector and the division of a neighbourhood).
References
| [1] | D. Hilbert, S.E. Cohn-Vossen, "Geometry and the imagination" , Chelsea (1952) (Translated from German) |
| [2] | H. Seifert, W. Threlfall, "A textbook of topology" , Acad. Press (1980) (Translated from German) |
| [3] | D.B. Fuks, A.T. Fomenko, V.L. Gutenmakher, "Homotopic topology" , Moscow (1969) (In Russian) |
One-sided and two-sided surfaces. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=One-sided_and_two-sided_surfaces&oldid=13217