Difference between revisions of "Heinz-Kato inequality"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (moved Heinz–Kato inequality to Heinz-Kato inequality: ascii title) |
(No difference)
| |
Revision as of 18:52, 24 March 2012
In the sequel, a capital letter denotes a bounded linear operator on a Hilbert space 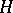 . An operator
. An operator 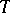 is said to be positive (denoted by
is said to be positive (denoted by 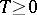 ) if
) if 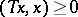 for all
for all 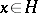 .
.
The Heinz–Kato inequality is an extension of the generalized Cauchy–Schwarz inequality (cf. also Cauchy inequality). It follows from the fact that
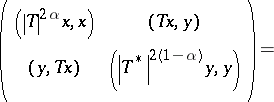 |
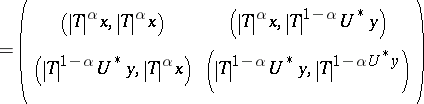 |
is non-negative, where 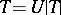 is the polar decomposition of
is the polar decomposition of  .
.
The Heinz–Kato inequality (1952; cf. [a4], [a3]): If  and
and 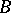 are positive operators such that
are positive operators such that 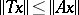 and
and  for all
for all 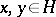 , then the following inequality holds for all
, then the following inequality holds for all 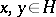 :
:
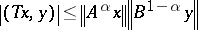 | (a1) |
for all 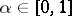 .
.
It is proved in [a1] that the Heinz–Kato inequality is equivalent to:
 | (a2) |
for arbitrary positive operators  and
and  .
.
The Heinz inequality yields the Heinz–Kato inequality.
On the other hand, it is shown in [a2] that the Löwner–Heinz inequality is equivalent to the following Cordes inequality (a3), although the first is an operator inequality and the latter is a norm inequality:
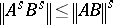 | (a3) |
for  and
and 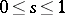 .
.
It is well known that the Heinz–Kato inequality (a1) is equivalent to the Löwner–Heinz inequality, so that the Heinz–Kato inequality, the Löwner–Heinz inequality and the Cordes inequality are mutually equivalent.
Additional references can be found in Heinz inequality.
References
| [a1] | M. Fujii, T. Furuta, "Löwner–Heinz, Cordes and Heinz–Kato inequalities" Math. Japon. , 38 (1993) pp. 73–78 |
| [a2] | T. Furuta, "Norm inequalities equivalent to Löwner–Heinz theorem" Rev. Math. Phys. , 1 (1989) pp. 135–137 |
| [a3] | T. Kato, "Notes on some inequalities for linear operators" Math. Ann. , 125 (1952) pp. 208–212 |
| [a4] | E. Heinz, "Beiträge zur Störungstheorie der Spektralzerlegung" Math. Ann. , 123 (1951) pp. 415–438 |
Heinz-Kato inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Heinz-Kato_inequality&oldid=16896