Zorn lemma
maximal principle
If in a non-empty partially ordered set 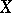 every totally ordered subset (cf. Totally ordered set) has an upper bound, then
every totally ordered subset (cf. Totally ordered set) has an upper bound, then 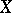 contains a maximal element. An element
contains a maximal element. An element 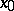 is called an upper bound of a subset
is called an upper bound of a subset 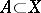 if
if  for all
for all 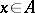 . If an upper bound for
. If an upper bound for 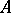 exists, then the set
exists, then the set 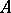 is said to be bounded above. An element
is said to be bounded above. An element 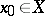 is called maximal in
is called maximal in 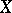 if there is no element
if there is no element 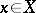 ,
, 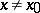 , such that
, such that 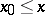 .
.
The lemma was stated and proved by M. Zorn in [1]. It is equivalent to the axiom of choice.
References
| [1] | M. Zorn, "A remark on a method in transfinite algebra" Bull. Amer. Math. Soc. , 41 (1935) pp. 667–670 |
| [2] | J.L. Kelley, "General topology" , Springer (1975) |
Comments
Earlier versions of the maximal principle, differing in detail from the one stated above but logically equivalent to it, were introduced independently by several mathematicians, the earliest being F. Hausdorff in 1909. For accounts of the history of the maximal principle, see [a1]–[a3].
References
| [a1] | P.J. Campbell, "The origin of "Zorn's lemma" " Historia Math. , 5 (1978) pp. 77–89 |
| [a2] | G.H. Moore, "Zermelo's axiom of choice" , Springer (1982) |
| [a3] | J. Rubin, H. Rubin, "Equivalents of the axiom of choice" , 1–2 , North-Holland (1963–1985) |
Zorn lemma. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Zorn_lemma&oldid=11582