Zeta-function
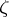 -function
-function
Zeta-functions in number theory are functions belonging to a class of analytic functions of a complex variable, comprising Riemann's zeta-function, its generalizations and analogues. Zeta-functions and their generalizations in the form of 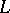 -functions (cf. Dirichlet
-functions (cf. Dirichlet  -function) form the basis of modern analytic number theory. In addition to Riemann's zeta-function one also distinguishes the generalized zeta-function
-function) form the basis of modern analytic number theory. In addition to Riemann's zeta-function one also distinguishes the generalized zeta-function 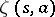 , the Dedekind zeta-function, the congruence zeta-function, etc.
, the Dedekind zeta-function, the congruence zeta-function, etc.
Riemann's zeta-function is defined by the Dirichlet series
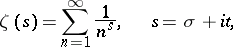 | (1) |
which converges absolutely and uniformly in any bounded domain of the complex  -plane for which
-plane for which 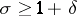 ,
, 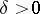 . If
. If 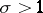 , a valid representation is the Euler product
, a valid representation is the Euler product
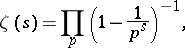 | (2) |
where 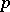 runs through all prime numbers.
runs through all prime numbers.
The identity of the series (1) and the product (2) is one of the fundamental properties of  . It makes it possible to obtain numerous relations connecting
. It makes it possible to obtain numerous relations connecting 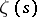 with important number-theoretic functions. E.g., if
with important number-theoretic functions. E.g., if 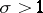 ,
,
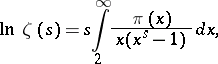 |
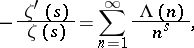 |
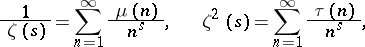 |
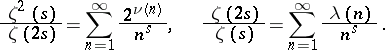 |
Here 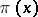 is the number of primes
is the number of primes 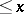 ,
, 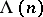 is the (von) Mangoldt function,
is the (von) Mangoldt function, 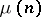 is the Möbius function,
is the Möbius function, 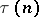 is the number divisors of the number
is the number divisors of the number  ,
, 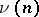 is the number of different prime factors of
is the number of different prime factors of  , and
, and 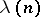 is the Liouville function. This accounts for the important role played by
is the Liouville function. This accounts for the important role played by  in number theory. As a function of a real variable,
in number theory. As a function of a real variable, 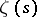 was introduced in 1737 by L. Euler [1], who proved that it could be expanded into the product (2). The function was subsequently studied by P.G.L. Dirichlet and also, with extraordinary success, by P.L. Chebyshev [2] in the context of the problem of the distribution of prime numbers. However, the most deeply intrinsic properties of
was introduced in 1737 by L. Euler [1], who proved that it could be expanded into the product (2). The function was subsequently studied by P.G.L. Dirichlet and also, with extraordinary success, by P.L. Chebyshev [2] in the context of the problem of the distribution of prime numbers. However, the most deeply intrinsic properties of 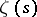 were discovered later, as a result of studying it as a function of a complex variable. This was first accomplished in 1876 by B. Riemann [3], who demonstrated the following assertions.
were discovered later, as a result of studying it as a function of a complex variable. This was first accomplished in 1876 by B. Riemann [3], who demonstrated the following assertions.
a)  permits analytic continuation to the whole complex
permits analytic continuation to the whole complex  -plane, in the form
-plane, in the form
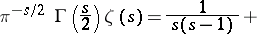 | (3) |
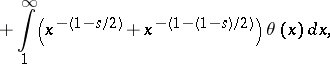 |
where 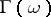 is the gamma-function and
is the gamma-function and
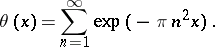 |
b) 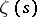 is a regular function for all values of
is a regular function for all values of  except for
except for 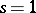 , where it has a simple pole with residue one, and it satisfies the functional equation
, where it has a simple pole with residue one, and it satisfies the functional equation
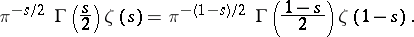 | (4) |
This equation is known as Riemann's functional equation. For the function
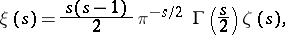 |
introduced by Riemann for studying the zeta-function and now known as Riemann's 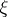 -function, this equation assumes the form
-function, this equation assumes the form
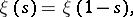 |
while if one puts
 |
it assumes the form
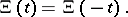 |
This last function 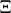 is distinguished by the fact that it is an even entire function which is real for real
is distinguished by the fact that it is an even entire function which is real for real 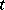 , and its zeros on the real axis correspond to the zeros of
, and its zeros on the real axis correspond to the zeros of 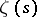 on the straight line
on the straight line 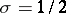 .
.
c) Since 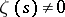 for
for 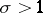 , by (4) this function has only simple zeros at the points
, by (4) this function has only simple zeros at the points 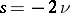 ,
, 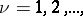 in the half-plane
in the half-plane 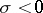 . These zeros are known as the trivial zeros of
. These zeros are known as the trivial zeros of 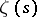 . Also,
. Also, 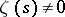 for
for 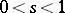 . Thus, all non-trivial zeros of
. Thus, all non-trivial zeros of 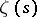 are complex numbers, lying symmetric with respect to both the real axis
are complex numbers, lying symmetric with respect to both the real axis 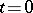 and the vertical line
and the vertical line 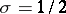 and situated inside the strip
and situated inside the strip 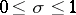 . This strip is known as the critical strip.
. This strip is known as the critical strip.
Riemann also stated the following hypotheses.
1) The number  of zeros of
of zeros of 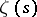 in the rectangle
in the rectangle 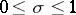 ,
, 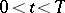 can be expressed by the formula
can be expressed by the formula
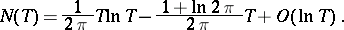 |
2) Let 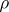 run through the non-trivial zeros of
run through the non-trivial zeros of 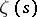 . Then the series
. Then the series 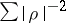 is convergent, while the series
is convergent, while the series 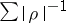 is divergent.
is divergent.
3) The function 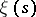 can be represented in the form
can be represented in the form
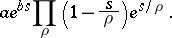 |
4) Let
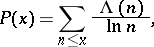 |
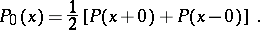 |
Then, for 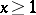 ,
,
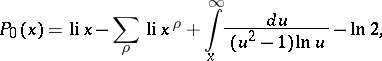 | (5) |
where  is the integral logarithm:
is the integral logarithm:
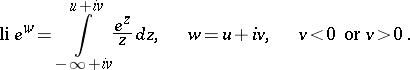 |
5) All non-trivial zeros of 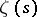 lie on the straight line
lie on the straight line 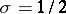 .
.
Subsequent to Riemann, the problem on the value distribution and, in particular, the zero distribution of the zeta-function became very widely known and was studied by a large number of workers. Riemann's hypotheses 2 and 3 were proved by J. Hadamard in 1893, and it was proved that, in hypothesis 3, 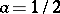 and
and 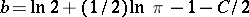 , where
, where 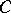 is the Euler constant; hypotheses 1 and 4 were established in 1894 by H. von Mangoldt, who also obtained the following important analogue of (5) for prime numbers. If
is the Euler constant; hypotheses 1 and 4 were established in 1894 by H. von Mangoldt, who also obtained the following important analogue of (5) for prime numbers. If
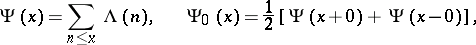 |
then, for 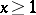 ,
,
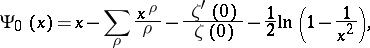 |
where 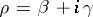 runs through the non-trivial zeros of
runs through the non-trivial zeros of 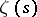 , while the symbol
, while the symbol 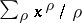 denotes the limit of the sum
denotes the limit of the sum 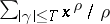 as
as 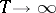 . This formula shows, similarly to formula (5), that the problem of the distribution of primes in the natural number series is closely connected with the location of the non-trivial zeros of the function
. This formula shows, similarly to formula (5), that the problem of the distribution of primes in the natural number series is closely connected with the location of the non-trivial zeros of the function 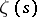 .
.
The last hypothesis (hypothesis 5) has not yet (1993) been proved or verified. This is the famous Riemann hypothesis on the zeros of the zeta-function.
The function 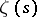 is unambiguously defined by its functional equation. More exactly, any function which can be represented by an ordinary Dirichlet series and which satisfies equation (4) coincides, under fairly broad conditions with respect to its regularity, with
is unambiguously defined by its functional equation. More exactly, any function which can be represented by an ordinary Dirichlet series and which satisfies equation (4) coincides, under fairly broad conditions with respect to its regularity, with 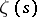 , up to a constant factor [4].
, up to a constant factor [4].
If
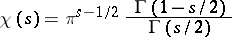 |
and 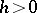 is constant, the approximate functional equation
is constant, the approximate functional equation
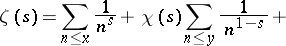 | (6) |
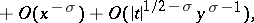 |
obtained in 1920 by G.H. Hardy and J.E. Littlewood [4], is valid for 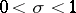 ,
, 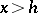 ,
, 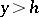 ,
, 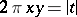 . This equation is important in the modern theory of the zeta-function and its applications. There exist general methods by which such results may be obtained not only for the class of zeta-functions, but in general for Dirichlet functions with a Riemann-type functional equation (3). The most complete result in this direction has been shown in [5]; in the case of
. This equation is important in the modern theory of the zeta-function and its applications. There exist general methods by which such results may be obtained not only for the class of zeta-functions, but in general for Dirichlet functions with a Riemann-type functional equation (3). The most complete result in this direction has been shown in [5]; in the case of 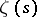 it leads, for any
it leads, for any  with
with 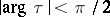 , to the relation
, to the relation
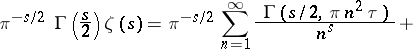 |
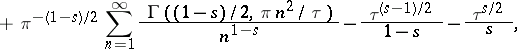 |
where 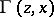 is the incomplete gamma-function. For
is the incomplete gamma-function. For
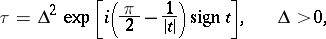 |
one obtains the approximate equation (6); for 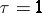 this relation becomes identical with the initial formula (3).
this relation becomes identical with the initial formula (3).
The principal problem in the theory of the zeta-function is the problem of the location of its non-trivial zeros and, in general, of its values within the range 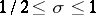 . The main directions of research conducted on the zeta-function include: the determination of the widest possible domain to the left of the straight line
. The main directions of research conducted on the zeta-function include: the determination of the widest possible domain to the left of the straight line 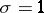 where
where 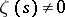 ; the problem of the order and of the average values of the zeta-function in the critical strip; estimates of the number of zeros of the zeta-function on the straight line
; the problem of the order and of the average values of the zeta-function in the critical strip; estimates of the number of zeros of the zeta-function on the straight line 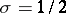 and outside it, etc.
and outside it, etc.
The first non-trivial result on the boundary for the zeros of the zeta-function was obtained in 1896 by Ch.J. de la Vallée-Poussin, who showed that there exists a constant 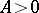 such that
such that
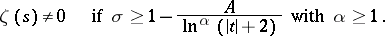 | (7) |
Other related approximations are connected with the approximate equation (6) and with the development of methods for estimating trigonometric sums.
The most powerful method for making estimates of this kind must be credited to I.M. Vinogradov (cf. Vinogradov method). The latest (to 1978) bound on the boundary of the zero-free domain for the zeta-function was obtained by Vinogradov in 1958 [7]. It is of the form (7) with 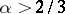 . The formula
. The formula
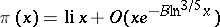 |
is the corresponding statement for prime numbers. There exists a certain connection between the growth of the modulus of the function 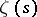 and the absence of zeros in a neighbourhood of the straight line
and the absence of zeros in a neighbourhood of the straight line 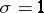 . Thus, (7) with
. Thus, (7) with 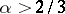 is the result of the estimates
is the result of the estimates
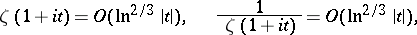 |
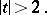 |
It is known, on the other hand [4], that
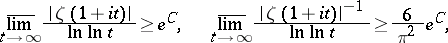 |
and, if Riemann's hypothesis is valid, these bounds should not exceed 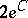 and
and 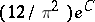 , respectively.
, respectively.
The order of the zeta-function in the critical strip is the greatest lower bound 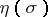 of the numbers
of the numbers  such that
such that 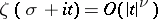 . If
. If 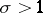 ,
,  , and if
, and if 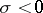 , then
, then 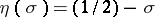 . The exact values of the function
. The exact values of the function 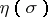 for
for 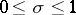 are unknown. According to the simplest assumption (the Lindelöf hypothesis)
are unknown. According to the simplest assumption (the Lindelöf hypothesis)
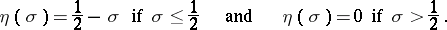 |
This is the equivalent to the statement that
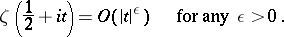 | (8) |
If  , the estimate
, the estimate 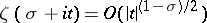 is valid.
is valid.
The most recent known estimate of 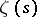 on the straight line
on the straight line 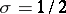 [4] deviates strongly from the expected estimate (8); it has the form
[4] deviates strongly from the expected estimate (8); it has the form
 |
The problem on the average value of the zeta-function consists in determining the properties of the function
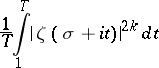 |
as  for any given
for any given 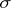 and
and 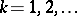 . The results have applications in the study of the zeros of the zeta-function, and in number theory directly.
. The results have applications in the study of the zeros of the zeta-function, and in number theory directly.
It has been proved [4] that
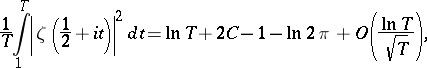 |
 |
If 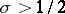 , [4],
, [4],
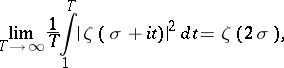 |
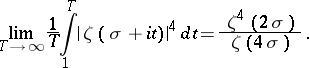 |
For 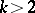 , all that is known is that if
, all that is known is that if 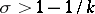 ,
,
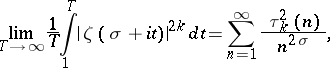 |
where  is the number of multiplicative representations of
is the number of multiplicative representations of  in the form of
in the form of 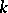 positive integers, and that the asymptotic relation
positive integers, and that the asymptotic relation
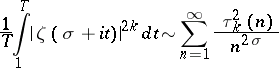 |
is the equivalent of Lindelöf's hypothesis for 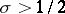 .
.
An important part in the theory of the zeta-function is played by the problem of estimating the function 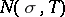 which denotes the number of zeros
which denotes the number of zeros 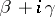 of
of 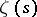 for
for  ,
, 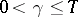 . Modern estimates of
. Modern estimates of 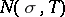 are based on convexity theorems of the average values of analytic functions, applied to the function
are based on convexity theorems of the average values of analytic functions, applied to the function
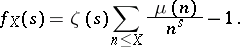 |
If, for some 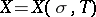 ,
, 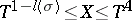 ,
,
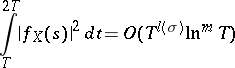 |
as 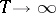 , uniformly for
, uniformly for 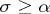 , where
, where  is a positive non-increasing function with bounded derivative and
is a positive non-increasing function with bounded derivative and 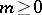 is a constant, then
is a constant, then
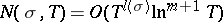 |
uniformly for 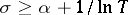 .
.
It is also known that if, for 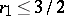 ,
,
 |
then, uniformly for  ,
,
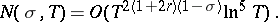 |
These two assumptions made it possible to obtain the following density theorems on the zeros of the zeta-function:
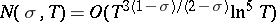 |
for  , and
, and
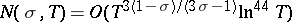 |
for  .
.
The zeros of the zeta-function on the straight line 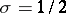 .
.
According to the Riemann hypothesis, all non-trivial zeros of the zeta-function lie on the straight line  . The fact that this straight line contains infinitely many zeros was first demonstrated in 1914 by Hardy [4] on the base of Ramanujan's formula:
. The fact that this straight line contains infinitely many zeros was first demonstrated in 1914 by Hardy [4] on the base of Ramanujan's formula:
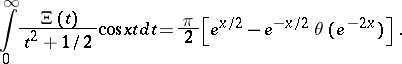 |
The latest result is to be credited to A. Selberg (1942) [4]: The number  of zeros of
of zeros of 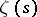 of the form
of the form 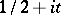 satisfies the inequality
satisfies the inequality
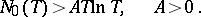 |
This means that the number of zeros of the zeta-function on the straight line 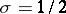 has the same order of increase as the number of all non-trivial zeros:
has the same order of increase as the number of all non-trivial zeros:
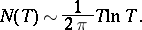 |
For the zeros of the zeta-function on this straight line, a number of other results are also known. The approximate functional equation actually makes it possible to compute (to a certain degree of accuracy) the values in which the zeta-function is zero closest to the real axis. With the aid of this method, a computer may be employed to find the zeros of 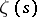 in the rectangle
in the rectangle  ,
, 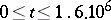 . Their number is
. Their number is 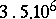 , and they all lie on the straight line
, and they all lie on the straight line  . The ordinates of the first six zero-points, accurate to within the second digit to the right of the decimal point, are 14.13; 21.02; 25.01; 30.42; 32.93; and 37.58.
. The ordinates of the first six zero-points, accurate to within the second digit to the right of the decimal point, are 14.13; 21.02; 25.01; 30.42; 32.93; and 37.58.
In general, the distance between contiguous zeros of 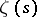 has been estimated in Littlewood's theorem (1924): For any sufficiently large
has been estimated in Littlewood's theorem (1924): For any sufficiently large 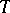 the function
the function  has a zero point
has a zero point  such that
such that
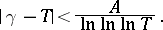 |
The generalized zeta-function is defined, for  , by the series
, by the series
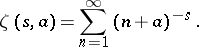 |
For 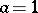 it becomes identical with Riemann's zeta-function. The analytic continuation to the entire plane is given by the formula
it becomes identical with Riemann's zeta-function. The analytic continuation to the entire plane is given by the formula
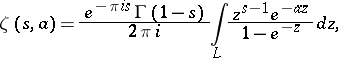 |
where the integral is taken over a contour 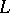 which is a path from infinity along the upper boundary of a section of the positive real axis up to some given
which is a path from infinity along the upper boundary of a section of the positive real axis up to some given 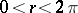 , then along the circle of radius
, then along the circle of radius  counterclockwise, and again to infinity along the lower boundary of the section. The function
counterclockwise, and again to infinity along the lower boundary of the section. The function 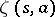 is regular everywhere except at the point
is regular everywhere except at the point 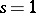 , at which it has a simple pole with residue one. It plays an important part in the theory of Dirichlet
, at which it has a simple pole with residue one. It plays an important part in the theory of Dirichlet 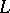 -functions [9], [10].
-functions [9], [10].
Dedekind's zeta-function is the analogue of Riemann's zeta-function for algebraic number fields, and was introduced by R. Dedekind [11].
Let 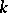 be an algebraic number field of degree
be an algebraic number field of degree 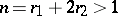 , where
, where 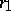 is the number of real fields and
is the number of real fields and 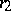 is the number of complex-conjugated pairs of fields in
is the number of complex-conjugated pairs of fields in 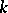 ; further, let
; further, let 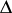 be the discriminant,
be the discriminant, 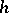 the number of divisor classes, and
the number of divisor classes, and 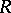 the regulator of the field
the regulator of the field 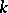 , and let
, and let  be the number of roots of unity contained in
be the number of roots of unity contained in 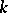 .
.
Dedekind's zeta-function 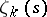 of the field
of the field 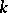 is the defined by the series
is the defined by the series
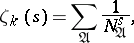 |
where 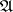 runs through all integral non-zero divisors of
runs through all integral non-zero divisors of 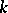 and
and  is the norm of the divisor
is the norm of the divisor 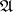 . This series converges absolutely and uniformly for
. This series converges absolutely and uniformly for 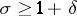 ,
, 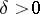 , defining an analytic function which is regular in the half-plane
, defining an analytic function which is regular in the half-plane 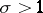 .
.
If  , then
, then
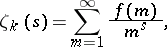 |
where 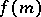 is the number of integral divisors of
is the number of integral divisors of 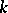 with norm
with norm 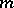 ;
; 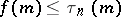 , where
, where 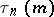 is the number of multiplicative representations of
is the number of multiplicative representations of 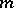 by
by  natural factors.
natural factors.
If  , Euler's identity
, Euler's identity
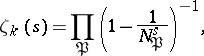 |
holds, where  runs through all prime divisors of
runs through all prime divisors of 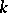 .
.
Main properties of Dedekind's zeta-function.
Cf. [11].
1) 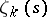 is regular in the entire complex plane except at the point
is regular in the entire complex plane except at the point 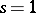 , at which it has a simple pole with residue
, at which it has a simple pole with residue
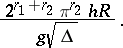 |
2) 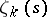 satisfies the functional equation
satisfies the functional equation
 |
where
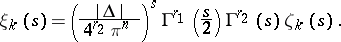 |
3) If 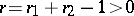 , the function
, the function 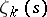 has a zero of order
has a zero of order  at the point
at the point 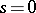 ;
; 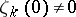 if
if  ; at the points
; at the points 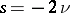 ,
, 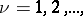 Dedekind's zeta-function
Dedekind's zeta-function  has zeros of order
has zeros of order 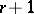 ; at the points
; at the points 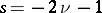 for
for 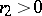 it has zeros of order
it has zeros of order 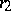 , while for
, while for 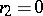 it is non-zero. These are the trivial zeros of the function
it is non-zero. These are the trivial zeros of the function 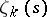 .
.
4) All other zeros of 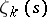 lie in the critical strip
lie in the critical strip 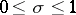 .
.
The basic hypothesis is that all non-trivial zeros of 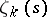 lie on the straight line
lie on the straight line 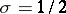 . It has been proved that
. It has been proved that 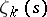 has no zeros on the straight line
has no zeros on the straight line 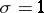 . Moreover, there exists an absolute positive constant
. Moreover, there exists an absolute positive constant 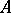 , as well as a constant
, as well as a constant 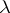 depending on the parameters of
depending on the parameters of 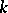 , with the following property:
, with the following property:
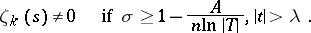 |
In general, if the parameters of 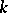 are given, many results analogous to those for Riemann's zeta-function apply to
are given, many results analogous to those for Riemann's zeta-function apply to 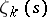 . However, in the general case the theory of Dedekind's zeta-function is more complicated, since it also comprises the theory of Dirichlet
. However, in the general case the theory of Dedekind's zeta-function is more complicated, since it also comprises the theory of Dirichlet 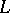 -functions. Thus, it is not yet (1978) known if Dedekind's zeta-functions have real zeros between 0 and 1. The exact dependence between Dedekind's zeta-functions and
-functions. Thus, it is not yet (1978) known if Dedekind's zeta-functions have real zeros between 0 and 1. The exact dependence between Dedekind's zeta-functions and 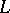 -series of a rational field has the following form. Let
-series of a rational field has the following form. Let 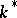 be the minimal Galois field containing
be the minimal Galois field containing 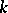 ; let
; let 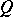 be the Galois group of
be the Galois group of 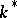 ,
, 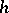 the class number of
the class number of 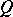 and
and 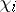 the prime characters of
the prime characters of 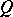 ,
, 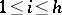 . Then
. Then
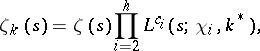 |
where 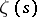 is Riemann's zeta-function,
is Riemann's zeta-function, 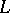 are Artin's
are Artin's 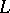 -series and
-series and 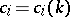 are positive integers determined by the properties of the relative group of the field
are positive integers determined by the properties of the relative group of the field 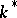 . In particular, if
. In particular, if 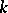 is a cyclotomic extension, then
is a cyclotomic extension, then 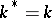 ,
, 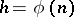 ,
, 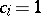 , and Artin's
, and Artin's 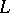 -series become ordinary Dirichlet
-series become ordinary Dirichlet 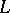 -series.
-series.
Dedekind's zeta-functions of a divisor class 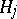 of the field
of the field 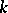 , denoted by
, denoted by 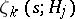 , are considered in parallel with Dedekind's zeta-function
, are considered in parallel with Dedekind's zeta-function 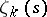 . These functions are defined by the same series as
. These functions are defined by the same series as 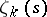 , but
, but 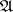 runs not through all, but only through the integral divisors belonging to the given class
runs not through all, but only through the integral divisors belonging to the given class 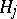 . The properties of the functions
. The properties of the functions  resemble those of
resemble those of 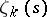 . The following formula is valid:
. The following formula is valid:
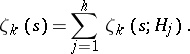 |
Dedekind's zeta-functions are the basis of the modern analytic theory of divisors of algebraic number fields. There they play the role played by Riemann's zeta-function in the theory of numbers of the rational field.
The congruence zeta-function or the Artin–Schmidt zeta-function (see Zeta-function in algebraic geometry, below) is the analogue of Dedekind's zeta-function for fields of algebraic functions in a single variable and with a finite field of constants.
References
| [1] | L. Euler, "Einleitung in die Analysis des Unendlichen" , Springer (1983) (Translated from Latin) |
| [2] | P.L. Chebyshev, "Selected mathematical works" , Moscow-Leningrad (1946) (In Russian) |
| [3] | B. Riemann, "Collected works" , Dover, reprint (1953) |
| [4] | E.C. Titchmarsh, "The theory of the Riemann zeta-function" , Clarendon Press (1986) ((Rev. ed.)) |
| [5] | A.F. Lavrik, "Approximate functional equations for Dirichlet functions" Math. USSR Izv. , 2 (1968) pp. 129–179 Izv. Akad. Nauk SSSR Ser. Mat. , 32 : 1 (1968) pp. 134–185 |
| [6] | I.M. Vinogradov, "The method of trigonometric sums in the theory of numbers" , Interscience (1954) (Translated from Russian) |
| [7] | I.M. Vinogradov, "A new estimate for  " Izv. Akad. Nauk. Ser. Mat. , 22 (1958) pp. 161–164 (In Russian) " Izv. Akad. Nauk. Ser. Mat. , 22 (1958) pp. 161–164 (In Russian) |
| [8] | H.L. Montgomery, "Zeros of  -functions" Invent. Math. , 8 (1969) pp. 346–354 -functions" Invent. Math. , 8 (1969) pp. 346–354 |
| [9] | K. Prachar, "Primzahlverteilung" , Springer (1957) |
| [10] | N.G. Chudakov, "Introductions to the theory of Dirichlet  -functions" , Moscow-Leningrad (1947) (In Russian) -functions" , Moscow-Leningrad (1947) (In Russian) |
| [11] | E. Hecke, "Mathematische Werke" , Vandenhoeck & Ruprecht (1959) |
Comments
To date (1993), the sharpest known zero-free region is given by the following theorem [a1]: There is an absolute constant 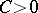 such that
such that 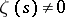 for
for
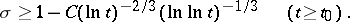 |
By numerical computations combined with analytic theory it has been shown that the first  non-trivial zeros of
non-trivial zeros of 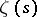 are precisely on the line
are precisely on the line 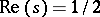 , [a4].
, [a4].
N. Levinson has shown that at least 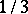 -rd of the non-trivial zeros of
-rd of the non-trivial zeros of 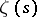 are indeed on
are indeed on 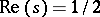 , [a5].
, [a5].
References
| [a1] | A. Ivic, "The Riemann zeta-function" , Wiley (1985) |
| [a2] | S.J. Patterson, "An introduction to the theory of the Riemann zeta-function" , Cambridge Univ. Press (1988) |
| [a3] | H.M. Edwards, "Riemann's zeta-function" , Acad. Press (1974) |
| [a4] | R.P. Brent, J. van de Lune, H.J.J. te Riele, D.T. Winter, "The first 200.000.001 zeros of Riemann's zeta-function" , Computational methods in number theory , Math. Centre , Amsterdam (1982) pp. 389–403 |
| [a5] | N. Levinson, "More than one third of the zeros of the Riemann zeta-function are on 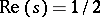 " Adv. Math. , 13 (1974) pp. 383–436 " Adv. Math. , 13 (1974) pp. 383–436 |
| [a6] | T.M. Apostol, "Introduction to analytic number theory" , Springer (1976) |
| [a7] | R. Dedekind, "Gesammelte Math. Werke" , 1–3 , Vieweg (1930–1932) |
| [a8] | G.H. Hardy, E.M. Wright, "An introduction to the theory of numbers" , Clarendon Press (1979) |
| [a9] | C.B. Haselgrove, J.C.P. Miller, "Tables of the Riemann zeta-function" , Cambridge Univ. Press (1960) |
| [a10] | E. Hecke, "Vorlesungen über die Theorie der algebraischen Zahlen" , Chelsea, reprint (1970) |
| [a11] | A. Ivic, "Topics in recent zeta-function theory" , Publ. Math. Orsay (1983) |
| [a12] | E. Landau, "Handbuch der Lehre von der Verteilung der Primzahlen" , Chelsea, reprint (1953) |
| [a13] | R.S. Lehman, "Separation of zeros of the Riemann zeta-function" Math. of Comp. , 20 (1966) pp. 523–541 |
| [a14] | H.J.J. te Riele, J. van de Lune, D.T. Winter, "On the zeros of the Riemann zeta-function in the critical strip IV" Math. of Comp. , 46 (1986) pp. 667–682 |
| [a15] | D.B. Zagier, "Zetafunktionen und quadratische Körper" , Springer (1981) |
The zeta-function in algebraic geometry is an analytic function of a complex variable  describing the arithmetic of algebraic varieties over finite fields and schemes of finite type over
describing the arithmetic of algebraic varieties over finite fields and schemes of finite type over 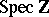 . If
. If 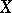 is such a scheme,
is such a scheme, 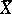 is the set of its closed points and
is the set of its closed points and 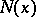 denotes the number of elements of the residue field
denotes the number of elements of the residue field 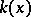 of a point
of a point  , then the zeta-function
, then the zeta-function 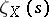 is given by the Euler product
is given by the Euler product
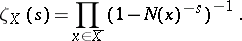 |
This converges absolutely if 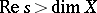 , it admits meromorphic continuation to the half-plane
, it admits meromorphic continuation to the half-plane 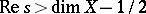 , and has a pole at the point
, and has a pole at the point 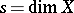 [10]. If
[10]. If  , then
, then 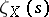 is Riemann's zeta-function, and if
is Riemann's zeta-function, and if 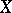 is finite over
is finite over 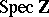 , then
, then 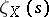 is Dedekind's zeta-function of the respective number field.
is Dedekind's zeta-function of the respective number field.
The situation when 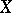 is an algebraic variety defined over a finite field
is an algebraic variety defined over a finite field 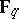 has been the most thoroughly studied. In this case
has been the most thoroughly studied. In this case
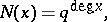 |
where 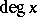 is the degree of the field
is the degree of the field  over the field
over the field 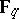 , and the function
, and the function 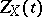 defined by
defined by
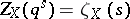 |
is usually considered instead of the function 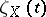 . If
. If 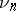 is the number of rational points of the variety
is the number of rational points of the variety  in the field
in the field 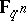 , it has been proved [14] that
, it has been proved [14] that
 |
Such zeta-functions were first introduced for the case of algebraic curves (in analogy with algebraic number fields) in 1924 by E. Artin [1], who noted that they are rational functions in 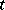 and that in certain cases an analogue of the Riemann hypothesis on zeros is valid for such functions. This analogue was named the Artin hypothesis. It was demonstrated in 1933 by H. Hasse for curves of genus one (for genus zero the situation is trivial), and by A. Weil (1940) for curves of arbitrary genus with the aid of results of the theory of Abelian varieties (cf. Abelian variety), mainly created by him with this purpose in view [2], [14].
and that in certain cases an analogue of the Riemann hypothesis on zeros is valid for such functions. This analogue was named the Artin hypothesis. It was demonstrated in 1933 by H. Hasse for curves of genus one (for genus zero the situation is trivial), and by A. Weil (1940) for curves of arbitrary genus with the aid of results of the theory of Abelian varieties (cf. Abelian variety), mainly created by him with this purpose in view [2], [14].
Weil [2] considered zeta-functions of arbitrary algebraic varieties and pointed out a hypothesis generalizing the then known results for curves. His studies are based on the observation that the set of points of the variety  which are rational in
which are rational in 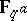 , is also the set of fixed points of the
, is also the set of fixed points of the  -th power of the Frobenius endomorphism of this variety. Weil's first conjecture says that the category of algebraic varieties over finite fields admits a cohomology theory which satisfies all the formal properties required to obtain the Lefschetz formula. If
-th power of the Frobenius endomorphism of this variety. Weil's first conjecture says that the category of algebraic varieties over finite fields admits a cohomology theory which satisfies all the formal properties required to obtain the Lefschetz formula. If 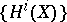 are the cohomology groups of such a theory, it follows from the Lefschetz formula that
are the cohomology groups of such a theory, it follows from the Lefschetz formula that
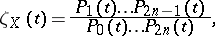 |
where 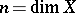 and
and 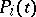 are the characteristic polynomials of the mapping induced by the Frobenius endomorphism on the Weil cohomology
are the characteristic polynomials of the mapping induced by the Frobenius endomorphism on the Weil cohomology 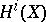 . In particular, the function
. In particular, the function  is rational.
is rational.
According to Weil's second conjecture, the function 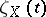 must satisfy a functional equation. For a smooth projective variety
must satisfy a functional equation. For a smooth projective variety 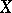 this equation reads
this equation reads
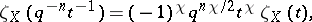 |
where 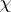 is the Euler characteristic, equal to
is the Euler characteristic, equal to 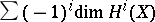 . (This hypothesis is a formal consequence of the existence of a cohomology.) B. Dwork [6] proved that the zeta-function is rational for all
. (This hypothesis is a formal consequence of the existence of a cohomology.) B. Dwork [6] proved that the zeta-function is rational for all 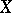 , using a method not involving cohomology. The cohomology theory predicted by Weil was created in 1958 by A. Grothendieck (cf. Weil cohomology; Topologized category;
, using a method not involving cohomology. The cohomology theory predicted by Weil was created in 1958 by A. Grothendieck (cf. Weil cohomology; Topologized category; 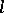 -adic cohomology). Grothendieck, together with M. Artin, demonstrated both Weil conjectures for smooth projective varieties, the polynomials
-adic cohomology). Grothendieck, together with M. Artin, demonstrated both Weil conjectures for smooth projective varieties, the polynomials 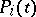 having, in general, integral
having, in general, integral 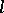 -adic coefficients which depend on the selection of the prime number
-adic coefficients which depend on the selection of the prime number 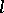 which forms the basis of the theory. It is assumed that the coefficients are in fact integers which are independent of
which forms the basis of the theory. It is assumed that the coefficients are in fact integers which are independent of 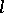 and, in general, of the choice of the cohomology theory. This postulate is widely known as Weil's third conjecture. Finally, Weil's fourth conjecture (and last one) refers to the zeros
and, in general, of the choice of the cohomology theory. This postulate is widely known as Weil's third conjecture. Finally, Weil's fourth conjecture (and last one) refers to the zeros 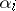 of the polynomials
of the polynomials 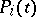 regarded as integral algebraic numbers (the Riemann hypothesis):
regarded as integral algebraic numbers (the Riemann hypothesis):
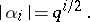 |
All these conjectures were demonstrated by P. Deligne [4].
The principal applications of Weil's conjectures in number theory deal with the study of congruences. Already in the case of curves, Weil's theorem entails the best estimate of a rational trigonometric sum in one variable [14]. These estimates were generalized to include sums involving any number of variables. Another important application of this theory are estimates of the Fourier coefficients of modular forms (cf. Modular form) (the Ramanujan–Peterson problem [4], [15]).
In fact, the above results are special cases of much more general theorems about arbitrary 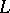 -functions connected with representations of Galois groups of coverings of the variety
-functions connected with representations of Galois groups of coverings of the variety 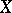 or, more generally, with some
or, more generally, with some 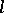 -adic sheaf on
-adic sheaf on 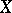 [5], [10]. These functions serve as analogues of the
[5], [10]. These functions serve as analogues of the 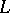 -functions known in the algebraic number theory on arbitrary schemes. Now, let
-functions known in the algebraic number theory on arbitrary schemes. Now, let 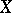 be a scheme of finite type over
be a scheme of finite type over 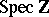 such that its general fibre
such that its general fibre 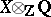 is a non-empty algebraic variety over the field of rational numbers
is a non-empty algebraic variety over the field of rational numbers 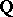 . One conjectures that the zeta-functions
. One conjectures that the zeta-functions 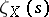 have meromorphic continuations to the entire
have meromorphic continuations to the entire  -plane and satisfy a functional equation. The hypothetical form of such an equation was proposed in [11]. However, at the time of writing (1978) the conjecture has been proved in very special cases only (rational surfaces, algebraic curves uniformizable by modular functions and Abelian varieties with complex multiplication [15]). As regards the analogue of the Riemann hypothesis, it has not even been formulated yet for the situation considered.
-plane and satisfy a functional equation. The hypothetical form of such an equation was proposed in [11]. However, at the time of writing (1978) the conjecture has been proved in very special cases only (rational surfaces, algebraic curves uniformizable by modular functions and Abelian varieties with complex multiplication [15]). As regards the analogue of the Riemann hypothesis, it has not even been formulated yet for the situation considered.
New ideas on the study of zeta-functions were contributed by J. Birch, P. Swinnerton-Dyer [12] and J. Tate [13]. In formulating the respective conjectures, it should be borne in mind that the function 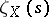 is the product of the zeta-functions
is the product of the zeta-functions 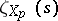 of the fibres
of the fibres 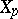 of the mapping
of the mapping 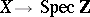 . These fibres, which are varieties over finite fields, can, according to Weil's conjecture, be decomposed into polynomials. Multiplying these expansions through, one obtains an analogous representation for the zeta-function:
. These fibres, which are varieties over finite fields, can, according to Weil's conjecture, be decomposed into polynomials. Multiplying these expansions through, one obtains an analogous representation for the zeta-function:
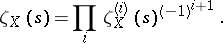 |
According to the conjecture of Birch and Swinnerton-Dyer, the order of the zero of the function 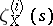 at the point
at the point 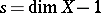 is equal to the rank of the group of rational points of the Picard variety
is equal to the rank of the group of rational points of the Picard variety 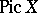 (which, by virtue of the Mordell–Weil theorem, is finite). Accordingly, this conjecture assumes that meromorphic continuation of the zeta-function is possible as conjectured.
(which, by virtue of the Mordell–Weil theorem, is finite). Accordingly, this conjecture assumes that meromorphic continuation of the zeta-function is possible as conjectured.
In its original form, the conjecture of Birch and Swinnerton-Dyer was demonstrated for elliptic curves over the field 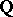 , as a result of the study of extensive tables of curves with complex multiplication [12]. Subsequently there was suggested a hypothetical value of the coefficient at the appropriate power of the variable
, as a result of the study of extensive tables of curves with complex multiplication [12]. Subsequently there was suggested a hypothetical value of the coefficient at the appropriate power of the variable  in the expansion of the function
in the expansion of the function  in a neighbourhood of the point
in a neighbourhood of the point 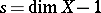 . It should be equal to
. It should be equal to
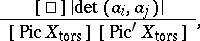 |
where  is the assumed finite order of the Shafarevich–Tate group of the locally trivial principal homogeneous space of the variety
is the assumed finite order of the Shafarevich–Tate group of the locally trivial principal homogeneous space of the variety 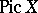 ,
, 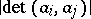 is the determinant of the bilinear form on the group of rational points of the variety
is the determinant of the bilinear form on the group of rational points of the variety  , which is obtained from the height (cf. Height, in Diophantine geometry) of points, and
, which is obtained from the height (cf. Height, in Diophantine geometry) of points, and 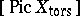 and
and 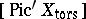 are the orders of the torsion subgroups in the group of rational points on
are the orders of the torsion subgroups in the group of rational points on 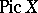 and the dual Abelian variety. This expression generalizes the expression for the residue of the Dedekind zeta-function at the point
and the dual Abelian variety. This expression generalizes the expression for the residue of the Dedekind zeta-function at the point 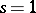 which is familiar in algebraic number theory. One difficulty involved in demonstrating the Birch–Swinnerton-Dyer conjecture is the fact that group
which is familiar in algebraic number theory. One difficulty involved in demonstrating the Birch–Swinnerton-Dyer conjecture is the fact that group  has not yet (1978) been fully computed for any curve. The analogue of the hypothesis has been proved for curves defined over a field of functions, but even in this case it had been necessary to assume the finiteness of the Brauer group, which here plays the role of the group
has not yet (1978) been fully computed for any curve. The analogue of the hypothesis has been proved for curves defined over a field of functions, but even in this case it had been necessary to assume the finiteness of the Brauer group, which here plays the role of the group  [5].
[5].
In his study of the action of the Galois group on algebraic cycles of varieties, Tate [13] proposed a conjecture on the poles of the functions 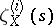 for even values of
for even values of 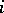 , to wit, that the function
, to wit, that the function 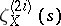 has, at the point
has, at the point 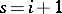 , a pole of order equal to the rank of the group of algebraic cycles of codimension
, a pole of order equal to the rank of the group of algebraic cycles of codimension 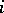 . This statement is closely connected with Tate's conjecture on algebraic cycles. For the various approaches leading to proofs of these conjectures, and for various arguments in favour of them, see [5], [7], [12], [13], [17].
. This statement is closely connected with Tate's conjecture on algebraic cycles. For the various approaches leading to proofs of these conjectures, and for various arguments in favour of them, see [5], [7], [12], [13], [17].
Quite apart from the concept of the zeta-function just described, zeta-functions which are Mellin transforms of modular forms have been studied in the theory of algebraic groups and automorphic functions. Weil noted in 1967 that a consequence of the general hypotheses on the function 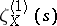 for an elliptic curve
for an elliptic curve 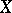 over
over 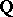 is that the curve
is that the curve 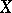 is uniformized by modular functions, while the function
is uniformized by modular functions, while the function 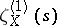 is the Mellin transform of the modular form corresponding to a differential of the first kind on
is the Mellin transform of the modular form corresponding to a differential of the first kind on  . This observation led to the assumption that the functions
. This observation led to the assumption that the functions 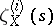 of any scheme
of any scheme 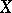 are Mellin transforms of the respective modular forms. Basic results on this problem were obtained by E. Jacquet and R. Langlands [7], [9]. In particular, they constructed an extensive class of Dirichlet series satisfying a certain functional equation and expandable into an Euler product which may be represented as the Mellin transform of modular forms on the group
are Mellin transforms of the respective modular forms. Basic results on this problem were obtained by E. Jacquet and R. Langlands [7], [9]. In particular, they constructed an extensive class of Dirichlet series satisfying a certain functional equation and expandable into an Euler product which may be represented as the Mellin transform of modular forms on the group 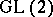 . Meeting the requirements of this theorem is directly related to the conjectures on the general properties of zeta-functions discussed above. Their verification is as yet possible only for curves defined over a field of functions.
. Meeting the requirements of this theorem is directly related to the conjectures on the general properties of zeta-functions discussed above. Their verification is as yet possible only for curves defined over a field of functions.
From 1970 on, the studies of 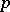 -adic zeta-functions of algebraic number fields [14] stimulated a similar approach to the zeta-functions of schemes — mainly elliptic curves. The problems involved, which greatly resemble those discussed above, are reviewed in [9]. The zeta-function of an elliptic curve over
-adic zeta-functions of algebraic number fields [14] stimulated a similar approach to the zeta-functions of schemes — mainly elliptic curves. The problems involved, which greatly resemble those discussed above, are reviewed in [9]. The zeta-function of an elliptic curve over 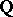 is closely connected with the one-dimensional formal group of the curve, and they completely define each other [16].
is closely connected with the one-dimensional formal group of the curve, and they completely define each other [16].
References
| [1] | E. Artin, "Quadratische Körper im Gebiet der höheren Kongruenzen I, II" Math. Z. , 19 (1924) pp. 153–246 |
| [2] | A. Weil, "Courbes algébriques et variétés abéliennes. Sur les courbes algébriques et les varietés qui s'en deduisent" , Hermann (1948) |
| [3] | A. Weil, "Numbers of solutions of equations in finite fields" Bull. Amer. Math. Soc. , 55 : 5 (1949) pp. 497–508 |
| [4] | P. Deligne, "La conjecture de Weil I" Publ. Math. IHES , 43 (1974) pp. 273–307 |
| [5] | A. Grothendieck (ed.) J. Giraud (ed.) et al. (ed.) , Dix exposés sur la cohomologie des schémas , North-Holland & Masson (1968) |
| [6] | B. Dwork, "A deformation theory for the zeta-function of a hypersurface" , Proc. Internat. Congress Mathematicians (Djursholm, 1963) , Almqvist & Weksell (1963) pp. 247–259 |
| [7] | E. Jacquet, "Automorphic forms on 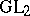 " , 1 , Springer (1970) " , 1 , Springer (1970) |
| [8] | Yu.I. Manin, "Cyclotomic fields and modular curves" Russian Math. Surveys , 26 : 6 (1971) pp. 7–78 Uspekhi Mat. Nauk , 26 : 6 (1971) pp. 7–71 |
| [9] | J.-P. Serre (ed.) P. Deligne (ed.) W. Kuyk (ed.) , Modular functions of one variable. 2–3 , Lect. notes in math. , 349; 350 , Springer (1973) |
| [10] | J.-P. Serre, "Zeta and 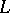 -functions" O.F.G. Schilling (ed.) , Arithmetical Algebraic geometry (Proc. Purdue Conf. 1963) , Harper & Row (1965) pp. 82–92 -functions" O.F.G. Schilling (ed.) , Arithmetical Algebraic geometry (Proc. Purdue Conf. 1963) , Harper & Row (1965) pp. 82–92 |
| [11] | J.-P. Serre, "Facteurs locaux des fonctions zêta des variétés algébriques (définitions et conjectures)" Sem. Delange–Pisot–Poitou , 19 (1969/70) |
| [12] | P. Swinnerton-Dyer, "The conjectures of Birch and Swinnerton-Dyer and of Tate" T.A. Springer (ed.) , Local Fields (Proc. Conf. Driebergen, 1966) , Springer (1967) pp. 132–157 |
| [13] | J.T. Tate, "Algebraic cycles and poles of zeta-functions" O.F.G. Schilling (ed.) , Arithmetical Algebraic geometry (Proc. Purdue Conf. 1963) , Harper & Row (1965) pp. 93–110 |
| [14] | I.R. Shafarevich, "The zeta-function" , Moscow (1969) (In Russian) |
| [15] | G. Shimura, "Introduction to the mathematical theory of automorphic functions" , Princeton Univ. Press (1971) |
| [16] | T. Honda, "Formal groups and zeta-functions" Osaka J. Math. , 5 (1968) pp. 199–213 |
| [17] | A.N. Parshin, "Arithmetic on algebraic varieties" J. Soviet Math. , 1 : 5 (1973) pp. 594–620 Itogi Nauk. Algebra. Topol. Geom. 1970 (1970/71) pp. 111–151 |
A.N. Parshin
Comments
The conjectures of Birch and Swinnerton-Dyer have been generalized by S. Bloch and P. Beilinson to conjectures relating the ranks of Chow groups obtained from algebraic cycles with orders of poles of zeta-functions. See [a6]–[a8].
The Tate–Shafarevich group of certain elliptic curves over number fields has recently been computed (–[a5]). As predicted, it is finite in these cases. The Weil conjectures and their proofs have been extended to the case of arbitrary schemes of finite type [a1].
References
| [a1] | P. Deligne, "La conjecture de Weil, II" Publ. Math. IHES , 52 (1980) pp. 137–252 |
| [a2] | E. Freitag, R. Kiehl, "Étale cohomology and the Weil conjecture" , Springer (1988) |
| [a3a] | V. Kolyvagin, "Finiteness of 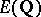 and and 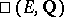 for a subclass of Weil curves" Math. USSR Izv. , 33 (1989) Izv. Akad. Nauk SSSR , 52 (1988) pp. 522–540 for a subclass of Weil curves" Math. USSR Izv. , 33 (1989) Izv. Akad. Nauk SSSR , 52 (1988) pp. 522–540 |
| [a3b] | V. Kolyvagin, "On the Mordell–Weil group and the Shafarevich–Tate group of Weil elliptic curves" Math. USSR Izv. , 33 (1989) Izv. Akad. Nauk SSSR , 52 (1988) pp. 1154–1180 |
| [a4] | V.A. Kolyvagin, "On the structure of the Shafarevich–Tate groups" S. Block (ed.) et al. (ed.) , Algebraic geometry , Lect. notes in math. , 1479 , Springer (1991) pp. 94–121 |
| [a5] | K. Rubin, "The Tate–Shafarevich group and 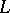 -functions of elliptic curves with complex multiplication" Invent. Math. , 89 (1987) pp. 527–560 -functions of elliptic curves with complex multiplication" Invent. Math. , 89 (1987) pp. 527–560 |
| [a6] | S. Bloch, "Algebraic cycles and values of 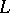 -functions I" J. Reine Angew. Math. , 350 (1984) pp. 94–108 -functions I" J. Reine Angew. Math. , 350 (1984) pp. 94–108 |
| [a7] | S. Bloch, "Algebraic cycles and values of  -functions II" Duke Math. J. , 52 (1985) pp. 379–397 -functions II" Duke Math. J. , 52 (1985) pp. 379–397 |
| [a8] | A. Beilinson, "Higher regulators and values of 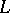 -functions" J. Soviet Math. , 30 (10985) pp. 2036–2070 Itogi Nauk. i Tekhn. Sovr. Probl. Mat. , 24 (1984) pp. 181–238 -functions" J. Soviet Math. , 30 (10985) pp. 2036–2070 Itogi Nauk. i Tekhn. Sovr. Probl. Mat. , 24 (1984) pp. 181–238 |
Zeta-function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Zeta-function&oldid=12363