Difference between revisions of "Zero"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 27: | Line 27: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> N. Jacobson, "Basic algebra" , '''1''' , Freeman (1974) {{MR|0356989}} {{ZBL|0284.16001}} </TD></TR></table> |
Revision as of 21:57, 30 March 2012
A (real or complex) number having the property that any number does not change if zero is added to it. It is denoted by the symbol  . The product of any number with zero is zero:
. The product of any number with zero is zero:
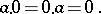 |
If the product of two numbers is zero, then one of them is zero (that is, 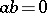 implies
implies 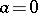 or
or 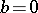 ). Division by zero is not defined. A direct generalization of this concept is that of the zero of an Abelian group.
). Division by zero is not defined. A direct generalization of this concept is that of the zero of an Abelian group.
The zero of an Abelian group 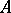 (in additive notation) is an element, also denoted by
(in additive notation) is an element, also denoted by  , satisfying
, satisfying 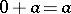 for all
for all 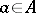 . It is uniquely determined.
. It is uniquely determined.
The zero of a ring (in particular, of a skew-field, i.e. division ring, or a field) is the zero of its additive group. The zero of a ring (like the number  ) has the property of absorption under multiplication:
) has the property of absorption under multiplication: 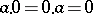 . However, in an arbitrary ring the product of two non-zero elements may be zero. Such elements are called zero divisors (cf. Zero divisor). Fields, skew-fields and integral domains do not have zero divisors.
. However, in an arbitrary ring the product of two non-zero elements may be zero. Such elements are called zero divisors (cf. Zero divisor). Fields, skew-fields and integral domains do not have zero divisors.
A left zero of a semi-group 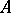 (in multiplicative notation) is an element
(in multiplicative notation) is an element 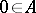 such that
such that 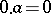 for all
for all 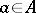 . A right zero is defined by the dual property. If a semi-group has a two-sided zero (an element which is both a left and a right zero), then this element is unique. The zero of a ring is also the zero of its multiplicative semi-group.
. A right zero is defined by the dual property. If a semi-group has a two-sided zero (an element which is both a left and a right zero), then this element is unique. The zero of a ring is also the zero of its multiplicative semi-group.
The zero of a lattice is its minimal element, if this exists. A complete lattice always has a zero: the intersection of all elements.
A zero of an algebraic system is an element picked out by a nullary operation (see Algebraic operation; Algebraic system). In the majority of examples considered above the zero is unique in the given system and even forms a one-element subsystem.
A zero is also called a null element.
For a zero object of a category, see Null object of a category.
The set of zeros of a function 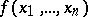 taking values in an Abelian group (ring, field, skew-field)
taking values in an Abelian group (ring, field, skew-field) 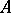 is the collection of values of the variables
is the collection of values of the variables 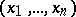 for which
for which 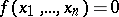 .
.
Comments
A subset of a topological space 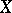 is called a zero set if it is the set of zeros of some continuous real-valued function on
is called a zero set if it is the set of zeros of some continuous real-valued function on 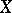 . Zero sets are an object of study in algebraic geometry (zero sets of systems of polynomials) and local analytic geometry (zero sets of systems of holomorphic functions and mappings).
. Zero sets are an object of study in algebraic geometry (zero sets of systems of polynomials) and local analytic geometry (zero sets of systems of holomorphic functions and mappings).
References
| [a1] | N. Jacobson, "Basic algebra" , 1 , Freeman (1974) MR0356989 Zbl 0284.16001 |
Zero. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Zero&oldid=17671