Zeckendorf representation
Every positive integer  can be expressed uniquely as a sum of distinct non-consecutive Fibonacci numbers. This result is called Zeckendorf's theorem and the sequence of Fibonacci numbers which add up to
can be expressed uniquely as a sum of distinct non-consecutive Fibonacci numbers. This result is called Zeckendorf's theorem and the sequence of Fibonacci numbers which add up to  is called the Zeckendorf representation of
is called the Zeckendorf representation of  . The theorem and the representation are named after the Belgian medical doctor and amateur mathematician E. Zeckendorf (1901–1983). See [a3] for a fine brief biography of Zeckendorf.
. The theorem and the representation are named after the Belgian medical doctor and amateur mathematician E. Zeckendorf (1901–1983). See [a3] for a fine brief biography of Zeckendorf.
The Fibonacci sequence is defined by  and
and  for
for  . The precise sequence used in the Zeckendorf theorem and representation is the Fibonacci sequence with
. The precise sequence used in the Zeckendorf theorem and representation is the Fibonacci sequence with  deleted, the first few members being
deleted, the first few members being
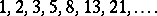 |
Examples of Zeckendorf representations are:
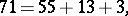 |
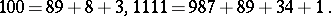 |
To construct the Zeckendorf representation of  , one chooses the largest Fibonacci number not greater than
, one chooses the largest Fibonacci number not greater than  , say
, say  , and subtracts it from
, and subtracts it from  . Unless
. Unless  is thereby reduced to zero, one then finds the largest Fibonacci number not greater than
is thereby reduced to zero, one then finds the largest Fibonacci number not greater than  , say
, say 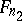 , and subtracts it, etc. If
, and subtracts it, etc. If  is reduced to zero after
is reduced to zero after 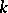 steps, one obtains a Zeckendorf representation of the form
steps, one obtains a Zeckendorf representation of the form
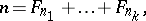 |
where  is a decreasing sequence of positive integers. This representation cannot include two consecutive Fibonacci numbers, say
is a decreasing sequence of positive integers. This representation cannot include two consecutive Fibonacci numbers, say 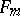 and
and 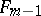 , for this would imply that their sum,
, for this would imply that their sum,  , or some larger Fibonacci number should have been chosen in place of
, or some larger Fibonacci number should have been chosen in place of 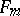 . The smallest integer whose Zeckendorf representation is the sum of
. The smallest integer whose Zeckendorf representation is the sum of  Fibonacci numbers is
Fibonacci numbers is
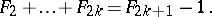 |
It can be shown by construction that no other sequence can be substituted for the Fibonacci sequence in the statement of Zeckendorf's theorem (see [a1]). Fibonacci numbers have been known to mathematics for some 800 years and it seems rather surprising that this property of them did not receive attention until relatively recently. Indeed, nothing appeared in print concerning the Zeckendorf representation until the middle of the 20th century, with the publication of a paper of C.G. Lekkerkerker [a4]. Zeckendorf did not publish his own account until 1972 (see [a6]) although (see [a3]) he had a proof of his theorem by 1939. Every positive integer can also be uniquely represented as a sum of different powers of two, and it is natural to compare Zeckendorf representations with binary representations. This is pursued in [a2], where there is a discussion of algorithms which, given two positive integers  and
and 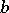 in Zeckendorf form, produce the Zeckendorf forms for
in Zeckendorf form, produce the Zeckendorf forms for 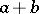 and
and  . Even the addition algorithm is rather more complicated than the corresponding algorithm for binary arithmetic. (If this were not so, "Zeckendorf arithmetic" might be used nowadays instead of binary arithmetic.) The Zeckendorf multiplication algorithm given in [a2] is based on the fact that, for
. Even the addition algorithm is rather more complicated than the corresponding algorithm for binary arithmetic. (If this were not so, "Zeckendorf arithmetic" might be used nowadays instead of binary arithmetic.) The Zeckendorf multiplication algorithm given in [a2] is based on the fact that, for 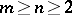 , the Zeckendorf representation of
, the Zeckendorf representation of  is
is
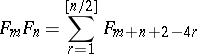 |
for  even. When
even. When  is odd, one has to add one further term to the above sum: the term
is odd, one has to add one further term to the above sum: the term 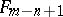 when
when 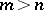 and the term
and the term 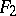 when
when  . In the upper limit of the summation,
. In the upper limit of the summation,  denotes the largest integer not greater than
denotes the largest integer not greater than 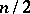 .
.
An amusing trivial "application" of the Zeckendorf representation is a method of converting miles into kilometres and vice versa without having to perform a multiplication. It relies on the coincidence that the number of kilometres in a mile (approximately 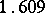 ) is close to the golden-section number (cf. also Golden ratio),
) is close to the golden-section number (cf. also Golden ratio),
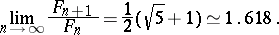 |
Thus, to convert miles into kilometres one writes down the (integer) number of miles in Zeckendorf form and replaces each of the Fibonacci numbers by its successor. This will give the Zeckendorf form of the corresponding approximate number of kilometres. For example,
 |
is approximately
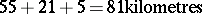 |
and  kilometres is approximately
kilometres is approximately
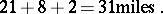 |
References
| [a1] | D.E. Daykin, "Representation of natural numbers as sums of generalised Fibonacci numbers" J. London Math. Soc. , 35 (1960) pp. 143–160 |
| [a2] | H. Freitag, G.M. Phillips, "Elements of Zeckendorf arithmetic" , Applications of Fibonacci Numbers (Graz, 1996) , 7 , Kluwer Acad. Publ. (1998) pp. 129–132 |
| [a3] | C. Kimberling, "Edouard Zeckendorf" Fibonacci Quart. , 36 (1998) pp. 416–418 |
| [a4] | C.G. Lekkerkerker, "Voorstelling van natuurlijke getallen door een som van getallen van Fibonacci" Simon Stevin , 29 (1952) pp. 190–195 |
| [a5] | S. Vajda, "Fibonacci & Lucas numbers, and the Golden Section" , Wiley (1989) |
| [a6] | E. Zeckendorf, "Représentation des nombres naturels par une somme de nombres de Fibonacci ou de nombres de Lucas" Bull. Soc. R. Sci. Liège , 41 (1972) pp. 179–182 |
Zeckendorf representation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Zeckendorf_representation&oldid=18410