Zahorski property
In his fundamental paper [a4], Z. Zahorski studied (among other topics) zero sets of approximately continuous functions (cf. Approximate continuity; the zero set of a real-valued function 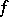 is the set of points at which the value of
is the set of points at which the value of 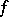 is precisely
is precisely  ). In modern language, Zahorski proved [a4], Lemma 11, that given a subset
). In modern language, Zahorski proved [a4], Lemma 11, that given a subset 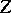 of the real line
of the real line 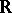 , there is an approximately continuous non-negative bounded function
, there is an approximately continuous non-negative bounded function 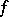 on
on 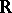 such that
such that 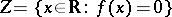 if and only if the set
if and only if the set 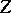 is of type
is of type 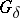 (cf. also Set of type
(cf. also Set of type 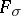 (
(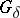 )) and closed in the density topology. (Recall that the density topology on
)) and closed in the density topology. (Recall that the density topology on 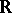 is formed by the collection of all Lebesgue measurable sets having each of their points as a density point.)
is formed by the collection of all Lebesgue measurable sets having each of their points as a density point.)
Notice that the class of approximately continuous functions was introduced by A. Denjoy in [a1] as a generalization of the notion of continuity. It is known that a function 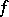 is approximately continuous if and only if
is approximately continuous if and only if 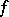 is continuous in the density topology. Functions that are approximately continuous have many pleasing properties. For example, they have the Darboux property and belong to the first Baire class (cf. Baire classes). Moreover, any bounded approximately continuous function is a derivative. Hence Zahorski's theorem can be used in constructing functions with peculiar behaviour. For example, it is easy to construct functions of Pompeiu type: A function
is continuous in the density topology. Functions that are approximately continuous have many pleasing properties. For example, they have the Darboux property and belong to the first Baire class (cf. Baire classes). Moreover, any bounded approximately continuous function is a derivative. Hence Zahorski's theorem can be used in constructing functions with peculiar behaviour. For example, it is easy to construct functions of Pompeiu type: A function 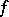 on
on 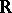 is a Pompeiu function if it has a bounded derivative
is a Pompeiu function if it has a bounded derivative 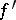 and if the sets on which
and if the sets on which 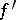 is zero or does not vanish, respectively, are both dense in
is zero or does not vanish, respectively, are both dense in 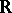 (cf. also Dense set). Also, Zahorski's theorem can serve as a main tool in proving a strengthened form of an old Ward's result from [a3]: Given a set
(cf. also Dense set). Also, Zahorski's theorem can serve as a main tool in proving a strengthened form of an old Ward's result from [a3]: Given a set 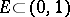 of Lebesgue measure zero, there is an approximately continuous function
of Lebesgue measure zero, there is an approximately continuous function 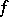 such that
such that 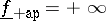 and
and 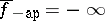 on
on  (here,
(here, 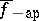 , respectively
, respectively  , denote the left-hand upper, respectively right-hand lower, approximative derivative of
, denote the left-hand upper, respectively right-hand lower, approximative derivative of 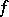 ).
).
Consider now a metric space 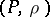 equipped with another topology
equipped with another topology  which is finer than the original metric topology
which is finer than the original metric topology  . The topology
. The topology  has the Luzin–Menshov property with respect to
has the Luzin–Menshov property with respect to 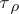 if for each pair of disjoint sets
if for each pair of disjoint sets 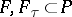 with
with 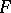
 -closed and
-closed and 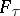
 -closed, there is a pair of disjoint sets
-closed, there is a pair of disjoint sets 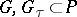 with
with 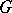
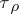 -open and
-open and 
 -open, such that
-open, such that 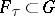 and
and 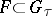 . If the topology
. If the topology  has the Luzin–Menshov property with respect to the metric topology, then it has the Zahorski property: Any
has the Luzin–Menshov property with respect to the metric topology, then it has the Zahorski property: Any  -closed subset of
-closed subset of 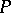 which is of the metric type
which is of the metric type 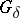 is the zero set of a bounded
is the zero set of a bounded  -continuous and metric upper semi-continuous function on
-continuous and metric upper semi-continuous function on 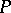 . Note that, conversely, the Zahorski property does not imply the Luzin–Menshov property. The density topology on the real line has the Luzin–Menshov property. Therefore it has the Zahorski property. Even very general density topologies, or also fine topologies of potential theory, have the Luzin–Menshov property, hence they have the Zahorski property as well.
. Note that, conversely, the Zahorski property does not imply the Luzin–Menshov property. The density topology on the real line has the Luzin–Menshov property. Therefore it has the Zahorski property. Even very general density topologies, or also fine topologies of potential theory, have the Luzin–Menshov property, hence they have the Zahorski property as well.
The Zahorski property can be introduced also in a very general framework of bitopological spaces. By this one understands a set 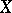 equipped with two topologies. If such a bitopological space satisfies the so-called "binormality condition" , it has the Zahorski property.
equipped with two topologies. If such a bitopological space satisfies the so-called "binormality condition" , it has the Zahorski property.
A detailed study of the Zahorski property and its applications is given in [a2].
References
| [a1] | A. Denjoy, "Sur les fonctions dérivées sommables" Bull. Soc. Math. France , 43 (1915) pp. 161–248 |
| [a2] | J. Lukeš, J. Malý, L. Zajíček, "Fine topology methods in real analysis and potential theory" , Lecture Notes in Mathematics , 1189 , Springer (1986) |
| [a3] | A.J. Ward, "On the points where 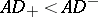 " J. London Math. Soc. , 8 (1933) pp. 293–299 " J. London Math. Soc. , 8 (1933) pp. 293–299 |
| [a4] | Z. Zahorski, "Sur la première dérivée" Trans. Amer. Math. Soc. , 69 (1950) pp. 1–54 |
Zahorski property. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Zahorski_property&oldid=16247