Young diagram
of order 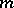
A graphical representation of a partition 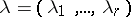 of a natural number
of a natural number 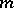 (where
(where 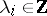 ,
, 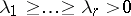 ,
, 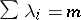 ). The Young diagram
). The Young diagram 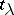 consists of
consists of 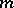 cells, arranged in rows and columns in such a way that the
cells, arranged in rows and columns in such a way that the 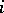 -th row has
-th row has 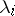 cells, where the first cell in each row lies in one (the first) column. E.g., the partition
cells, where the first cell in each row lies in one (the first) column. E.g., the partition 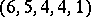 of 20 is represented by the Young diagram (cf. the diagram on the left).
of 20 is represented by the Young diagram (cf. the diagram on the left).
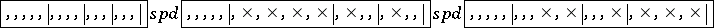 |
The transposed Young diagram 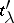 corresponds to the conjugate partition
corresponds to the conjugate partition 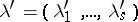 , where
, where  is the number of cells in the
is the number of cells in the 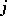 -th column of the Young diagram. Thus, in the example given above the conjugate partition will be
-th column of the Young diagram. Thus, in the example given above the conjugate partition will be  .
.
Each cell of a Young diagram defines two sets of cells, known as a hook and a skew-hook. Let 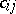 be the cell situated in the
be the cell situated in the 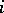 -th row and the
-th row and the 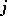 -th column of a given Young diagram. The hook
-th column of a given Young diagram. The hook 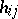 corresponding to it is the set consisting of all cells
corresponding to it is the set consisting of all cells 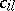 ,
, 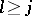 , and
, and 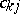 ,
, 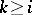 , while the skew-hook is the least connected set of border cells including the last cell of the
, while the skew-hook is the least connected set of border cells including the last cell of the 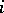 -th row and the last cell of the
-th row and the last cell of the 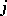 -th column. E.g. for the Young diagram chosen on the left, the hook and skew-hook corresponding to the cell
-th column. E.g. for the Young diagram chosen on the left, the hook and skew-hook corresponding to the cell  have the shape shown in the centre and on the right of the figure.
have the shape shown in the centre and on the right of the figure.
The length of a hook (respectively, a skew-hook) is understood to be the number of its cells. The length of the hook 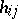 is
is 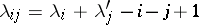 . By removing from a Young diagram a skew-hook of length
. By removing from a Young diagram a skew-hook of length 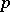 one obtains a Young diagram of order
one obtains a Young diagram of order 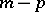 . The height of a hook (respectively, a skew-hook) is understood to be the number of rows over which the hook (skew-hook) is distributed.
. The height of a hook (respectively, a skew-hook) is understood to be the number of rows over which the hook (skew-hook) is distributed.
The language of Young diagrams and Young tableaux (cf. Young tableau) is applied in the representation of the symmetric groups and in the representation of the classical groups. It was proposed by A. Young (cf. ).
References
| [1a] | A. Young, "On quantitative substitutional analysis" Proc. London Math. Soc. , 33 (1901) pp. 97–146 |
| [1b] | A. Young, "On quantitative substitutional analysis" Proc. London Math. Soc. , 34 (1902) pp. 361–397 |
Comments
A Young diagram is also known as a Ferrers diagram in the West.
References
| [a1] | A. Kerber, G.D. James, "The representation theory of the symmetric group" , Addison-Wesley (1981) |
| [a2] | A. Kerber, "Algebraic combinatorics via finite group actions" , B.I. Wissenschaftsverlag Mannheim (1991) |
| [a3] | G.E. Andrews, "The theory of partitions" , Addison-Wesley (1976) |
| [a4] | I.G. Macdonald, "Symmetric functions and Hall polynomials" , Clarendon Press (1979) |
Young diagram. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Young_diagram&oldid=11674