Wronskian
Wronski determinant
The determinant of a system of  vector-functions of dimension
vector-functions of dimension  ,
,
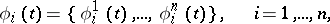 | (1) |
of the type
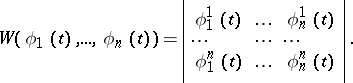 |
The Wronskian of a system of  scalar functions
scalar functions
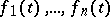 | (2) |
which have derivatives up to order 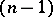 (inclusive) is the determinant
(inclusive) is the determinant
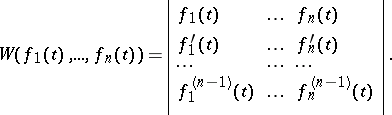 | (3) |
The concept was first introduced by J. Wronski [1].
If the vector-functions (1) are linearly dependent on a set 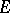 , then
, then
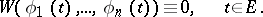 |
If the scalar functions (2) are linearly dependent on a set  , then
, then
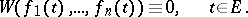 |
The converse theorems are usually not true: Identical vanishing of a Wronskian on some set is not a sufficient condition for linear dependence of  functions on this set.
functions on this set.
Let the vector-functions (1) be the solutions of a linear homogeneous  -th order system
-th order system 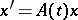 ,
,  , with an
, with an  -dimensional matrix
-dimensional matrix 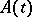 that is continuous on an interval
that is continuous on an interval 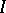 . If these solutions constitute a fundamental system, then
. If these solutions constitute a fundamental system, then
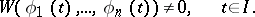 |
If the Wronskian of these solutions is equal to zero in at least one point of 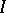 , it is identically equal to zero on
, it is identically equal to zero on 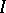 , and the functions (1) are linearly dependent. The Liouville formula
, and the functions (1) are linearly dependent. The Liouville formula
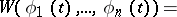 |
 |
where 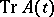 is the trace of the matrix
is the trace of the matrix 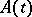 , is applicable.
, is applicable.
Let the functions (2) be the solutions of a linear homogeneous  -th order equation
-th order equation
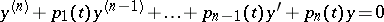 |
with continuous coefficients on the interval 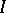 . If these solutions constitute a fundamental system, then
. If these solutions constitute a fundamental system, then
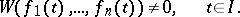 |
If the Wronskian of these solutions is zero in at least one point of  , it is identically equal to zero on
, it is identically equal to zero on 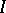 , and the functions (2) are linearly dependent. The Liouville formula
, and the functions (2) are linearly dependent. The Liouville formula
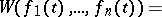 |
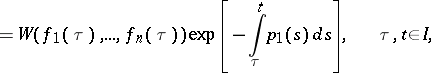 |
applies.
References
| [1] | J. Hoene-Wronski, "Réfutation de la théorie des fonctions analytiques de Lagrange" , Paris (1812) |
| [2] | L.S. Pontryagin, "Ordinary differential equations" , Addison-Wesley (1962) (Translated from Russian) |
Comments
An example of  functions (2) that are not linearly dependent but with vanishing Wronskian was given by G. Peano, [a3].
functions (2) that are not linearly dependent but with vanishing Wronskian was given by G. Peano, [a3].
A sub-Wronskian of order 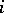 for
for 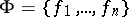 is obtained by taking the Wronskian of a subset of size
is obtained by taking the Wronskian of a subset of size 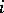 of
of 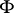 . Two theorems giving sufficient conditions for linear dependence in terms of Wronskians are as follows. 1) Let
. Two theorems giving sufficient conditions for linear dependence in terms of Wronskians are as follows. 1) Let 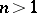 ,
, 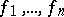 analytic and
analytic and 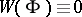 , then the
, then the 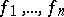 are linearly dependent, [a4], [a5]. 2) Let
are linearly dependent, [a4], [a5]. 2) Let  ,
, 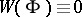 , but at no point of the interval of definition of
, but at no point of the interval of definition of 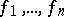 do all sub-Wronskians of order
do all sub-Wronskians of order 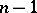 vanish simultaneously, then
vanish simultaneously, then 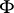 is linearly dependent, [a3].
is linearly dependent, [a3].
For more information and results concerning functions of several variables, cf. [a6], [a7].
References
| [a1] | T.M. Apostol, "Mathematical analysis" , Addison-Wesley (1974) |
| [a2] | P. Hartman, "Ordinary differential equations" , Birkhäuser (1982) |
| [a3] | G. Peano, "Sur le déterminant Wronskian" Mathesis , 9 (1989) pp. 75–76 |
| [a4] | M. Böcher, "Certain cases in which the vanishing of the Wronskian is a sufficient condition for linear dependence" Trans. Amer. Math. Soc. , 2 (1901) pp. 139–149 |
| [a5] | D.R. Curtis, "The vanishing of the Wronskian and the problem of linear dependence" Math. Ann. , 65 (1908) pp. 282–298 |
| [a6] | K. Wolsson, "A condition equivalent to linear dependence for functions with vanishing Wronskian" Linear Alg. Appl. , 116 (1989) pp. 1–8 |
| [a7] | K. Wolsson, "Linear dependence of a function set of  variables with vanishing generalized Wronskians" Linear Alg. Appl. , 117 (1989) pp. 73–80 variables with vanishing generalized Wronskians" Linear Alg. Appl. , 117 (1989) pp. 73–80 |
Wronskian. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Wronskian&oldid=17717