Word
A (linear) sequence of letters (cf. Letter) from some alphabet. For example, the series of symbols "wordinanalphabet" is a word in any alphabet containing the letters i, w, o, r, d, n, a, l, p, h, b, e, t. For convenience, one also allows the empty word, that is, the word containing no letters. It is a word in any alphabet.
More precisely, one can use an inductive characterization of a word, whereby the words in an alphabet  are defined as the objects obtained by the following generating process: a) the empty word is a word in
are defined as the objects obtained by the following generating process: a) the empty word is a word in  ; b) if an object
; b) if an object  is a word in
is a word in  and
and  is a letter of
is a letter of  , then the object
, then the object  is also a word in
is also a word in  . This characterization of words makes it possible to apply inductive arguments in proving universally true statements about the words in a given alphabet.
. This characterization of words makes it possible to apply inductive arguments in proving universally true statements about the words in a given alphabet.
A word is a fairly general type of constructive object, and because of this, the notion of a word plays an important role in constructive mathematics. The concept of a word is also widely used in algebra, mathematical linguistics and elsewhere.
References
| [1] | A.A. Markov, "Theory of algorithms" , Israel Program Sci. Transl. (1961) (Translated from Russian) (Also: Trudy Mat. Inst. Steklov. 42 (1954)) |
| [2] | A.A. Markov, N.M. [N.M. Nagornyi] Nagorny, "The theory of algorithms" , Kluwer (1988) (Translated from Russian) |
Comments
In algebra, words normally consist of letters and operation symbols, as "x+y-z" .
The length of a word is defined inductively:  ,
,  .
.
Under concatenation
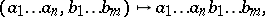 |
the set 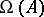 of all words in an alphabet
of all words in an alphabet 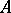 becomes an associative monoid. The empty word is the unit element. This is the free monoid over
becomes an associative monoid. The empty word is the unit element. This is the free monoid over  . It satisfies the freeness property: For every monoid
. It satisfies the freeness property: For every monoid 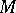 and mapping of sets
and mapping of sets 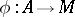 there is a unique morphism of monoids
there is a unique morphism of monoids 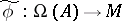 extending
extending 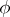 . Here,
. Here,  is identified with the set of words of length
is identified with the set of words of length  in
in  .
.
References
| [a1] | R.C. Lyndon, P.E. Schupp, "Combinatorial group theory" , Springer (1977) |
Word. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Word&oldid=16569