Wodzicki residue
non-commutative residue
In algebraic quantum field theory (cf. also Quantum field theory), in order to write down an action in operator language one needs a functional that replaces integration [a1]. For the Yang–Mills theory (cf. Yang–Mills field) this is the Dixmier trace, which is the unique extension of the usual trace to the ideal  of the compact operators
of the compact operators  such that the partial sums of its spectrum diverge logarithmically as the number of terms in the sum. The Wodzicki (or non-commutative) residue [a3] is the only extension of the Dixmier trace to the class of pseudo-differential operators (
such that the partial sums of its spectrum diverge logarithmically as the number of terms in the sum. The Wodzicki (or non-commutative) residue [a3] is the only extension of the Dixmier trace to the class of pseudo-differential operators ( DOs; cf. Pseudo-differential operator) which are not in
DOs; cf. Pseudo-differential operator) which are not in  . It is the only trace one can define in the algebra of
. It is the only trace one can define in the algebra of  DOs (up to a multiplicative constant), its definition being:
DOs (up to a multiplicative constant), its definition being:  , with
, with  the Laplace operator. It satisfies the trace condition:
the Laplace operator. It satisfies the trace condition:  . A very important property is that it can be expressed as an integral (local form):
. A very important property is that it can be expressed as an integral (local form):
 |
with  the co-sphere bundle on
the co-sphere bundle on  (some authors put a coefficient in front of the integral, this gives the Adler–Manin residue).
(some authors put a coefficient in front of the integral, this gives the Adler–Manin residue).
If 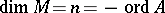 (
( a compact Riemannian manifold,
a compact Riemannian manifold,  an elliptic operator,
an elliptic operator,  ), it coincides with the Dixmier trace, and one has
), it coincides with the Dixmier trace, and one has
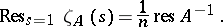 |
The Wodzicki residue continues to make sense for  DOs of arbitrary order and, even if the symbols
DOs of arbitrary order and, even if the symbols  ,
,  , are not invariant under coordinate choice, their integral is, and defines a trace. All residues at poles of the zeta-function of a
, are not invariant under coordinate choice, their integral is, and defines a trace. All residues at poles of the zeta-function of a 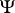 DO can be easily obtained from the Wodzicki residue [a2].
DO can be easily obtained from the Wodzicki residue [a2].
References
| [a1] | A. Connes, "Noncommutative geometry" , Acad. Press (1994) |
| [a2] | E. Elizalde, "Complete determination of the singularity structure of zeta functions" J. Phys. , A30 (1997) pp. 2735 |
| [a3] | M. Wodzicki, "Noncommutative residue I" Yu.I. Manin (ed.) , K-Theory, Arithmetic and Geometry , Lecture Notes in Mathematics , 1289 , Springer (1987) pp. 320–399 |
Wodzicki residue. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Wodzicki_residue&oldid=18226