Williamson matrices
A Hadamard matrix of order  is an
is an 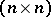 -matrix
-matrix 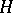 with as entries
with as entries 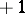 and
and 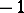 such that
such that 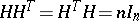 , where
, where  is the transposed matrix of
is the transposed matrix of 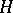 and
and 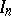 is the unit matrix of order
is the unit matrix of order  . Note that the problem of constructing Hadamard matrices of all orders
. Note that the problem of constructing Hadamard matrices of all orders 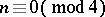 is as yet unsolved (1998; the first open case is
is as yet unsolved (1998; the first open case is 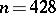 ). For a number of methods for constructing Hadamard matrices of concrete orders, see [a1], [a9], [a7]. One of these methods, described below, is due to J. Williamson [a10]. Let
). For a number of methods for constructing Hadamard matrices of concrete orders, see [a1], [a9], [a7]. One of these methods, described below, is due to J. Williamson [a10]. Let 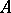 ,
, 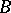 ,
, 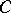 , and
, and 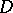 be pairwise commuting symmetric circulant
be pairwise commuting symmetric circulant 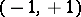 -matrices of order
-matrices of order 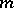 such that
such that 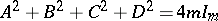 (such matrices are called Williamson matrices). Then the Williamson array
(such matrices are called Williamson matrices). Then the Williamson array
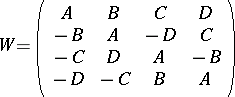 |
is a Hadamard matrix of order 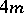 . The recent achievements about the construction of Hadamard matrices are connected with the construction of orthogonal designs [a4] (cf. also Design with mutually orthogonal resolutions), Baumert–Hall arrays [a2], Goethals–Seidel arrays [a5] and Plotkin arrays [a6], and with the construction of Williamson-type matrices, i.e., of four or eight
. The recent achievements about the construction of Hadamard matrices are connected with the construction of orthogonal designs [a4] (cf. also Design with mutually orthogonal resolutions), Baumert–Hall arrays [a2], Goethals–Seidel arrays [a5] and Plotkin arrays [a6], and with the construction of Williamson-type matrices, i.e., of four or eight 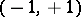 -matrices
-matrices 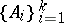 ,
, 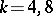 , of order
, of order 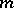 that satisfy the following conditions:
that satisfy the following conditions:
i) 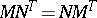 ,
, 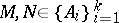 ;
;
ii) 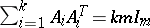 . Williamson-four matrices have been constructed for all orders
. Williamson-four matrices have been constructed for all orders 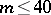 , with the exception of
, with the exception of 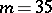 , which was eliminated by D.Z. Djokovic [a3], by means of an exhaustive computer search. It is worth mentioning that Williamson-type-four matrices of order
, which was eliminated by D.Z. Djokovic [a3], by means of an exhaustive computer search. It is worth mentioning that Williamson-type-four matrices of order 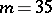 are not yet known (1998). Williamson-four and Williamson-type-four matrices are known for many values of
are not yet known (1998). Williamson-four and Williamson-type-four matrices are known for many values of 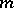 . For details, see [a9], Table A1; pp. 543–547. The most recent results can be found in [a11].
. For details, see [a9], Table A1; pp. 543–547. The most recent results can be found in [a11].
There are known Williamson-type-eight matrices of the orders 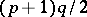 , where
, where 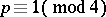 ,
, 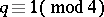 are prime numbers [a8].
are prime numbers [a8].
A set of 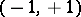 -matrices
-matrices  is called a Williamson family, of type
is called a Williamson family, of type 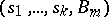 , if the following conditions are fulfilled:
, if the following conditions are fulfilled:
a) There exists a 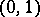 -matrix
-matrix 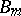 of order
of order 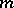 such that for arbitrary
such that for arbitrary 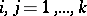 ,
, 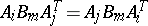 ;
;
b) 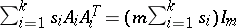 . If
. If 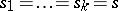 , then the type
, then the type 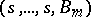 is denoted by
is denoted by 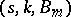 .
.
If 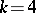 ,
, 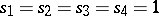 , and
, and 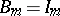 , then each Williamson family of type
, then each Williamson family of type 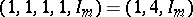 coincides with a family of Williamson-type matrices.
coincides with a family of Williamson-type matrices.
If 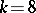 ,
, 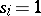 for
for 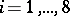 , and
, and 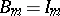 , then each Williamson family of type
, then each Williamson family of type  coincides with a family of Williamson-type-eight matrices.
coincides with a family of Williamson-type-eight matrices.
If 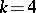 ,
, 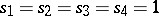 , and
, and 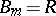 ,
, 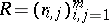 ,
,
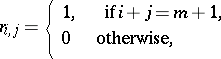 |
and 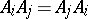 , then each Williamson family of type
, then each Williamson family of type 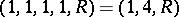 coincides with a family of generalized Williamson-type matrices.
coincides with a family of generalized Williamson-type matrices.
An orthogonal design of order  and type
and type 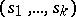 (
(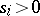 ) on commuting variables
) on commuting variables  is an
is an 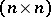 -matrix
-matrix 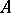 with entries from
with entries from 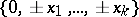 such that
such that
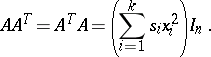 |
Let 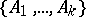 be a Williamson family of type
be a Williamson family of type 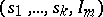 and suppose there exists an orthogonal design of type
and suppose there exists an orthogonal design of type 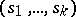 and order
and order  that consists of elements
that consists of elements 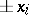 ,
, 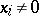 . Then there exists a Hadamard matrix of order
. Then there exists a Hadamard matrix of order 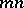 . In other words, the existence of orthogonal designs and Williamson families implies the existence of Hadamard matrices. For more details and further constructions see [a4], [a9].
. In other words, the existence of orthogonal designs and Williamson families implies the existence of Hadamard matrices. For more details and further constructions see [a4], [a9].
References
| [a1] | S.S. Agaian, "Hadamard matrices and their applications" , Lecture Notes Math. , 1168 , Springer (1985) |
| [a2] | L.D. Baumert, M. Hall Jr., "A new construction for Hadamard matrices" Bull. Amer. Math. Soc. , 71 (1965) pp. 169–170 |
| [a3] | D.Z. Djokovic, "Williamson matrices of order 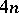 for for 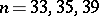 " Discrete Math. , 115 (1993) pp. 267–271 " Discrete Math. , 115 (1993) pp. 267–271 |
| [a4] | A.V. Geramita, J. Seberry, "Orthogonal designs: Quadratic forms and Hadamard matrices" , M. Dekker (1979) |
| [a5] | J.M. Goethals, J.J. Seidel, "A skew–Hadamard matrix of order 36" J. Austral. Math. Soc. A , 11 (1970) pp. 343–344 |
| [a6] | M. Plotkin, "Decomposition of Hadamard matrices" J. Combin. Th. A , 2 (1972) pp. 127–130 |
| [a7] | W.D. Wallis, A.P. Street, J.S. Wallis, "Combinatorics: Room squares, sum-free sets and Hadamard matrices" , Lecture Notes Math. , 292 , Springer (1972) |
| [a8] | J.S. Wallis, "Construction of Williamson type matrices" Linear and Multilinear Algebra , 3 (1975) pp. 197–207 |
| [a9] | J. Seberry, M. Yamada, "Hadamard matrices, sequences and block designs" J.H. Dinitz (ed.) D.R. Stinson (ed.) , Contemporary Design Theory: A Collection of Surveys , Wiley (1992) pp. 431–560 |
| [a10] | J. Williamson, "Hadamard's determinant theorem and the sum of four squares" Duke Math. J. , 11 (1944) pp. 65–81 |
| [a11] | M.Y. Xia, "An infinite class of supplementary difference sets and Williamson matrices" J. Combin. Th. A , 58 (1991) pp. 310–317 |
Williamson matrices. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Williamson_matrices&oldid=11318