Wigner-Weyl transform
Weyl–Wigner transform
Let  ,
,  , be a ray in
, be a ray in  . Then, for each
. Then, for each  , the Wigner transform of
, the Wigner transform of  is
is
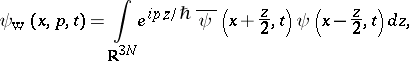 |
where  is Planck's constant. The quantity
is Planck's constant. The quantity  is called the Wigner function. It was introduced by E.P. Wigner in 1932, [a1], who interpreted
is called the Wigner function. It was introduced by E.P. Wigner in 1932, [a1], who interpreted  as a quasi-probability density in the phase space
as a quasi-probability density in the phase space 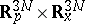 and showed that it obeyed a kinetic pseudo-differential equation (the Wigner equation) of the form
and showed that it obeyed a kinetic pseudo-differential equation (the Wigner equation) of the form 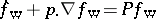 , where
, where 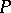 is a pseudo-differential operator with symbol defined by the potential energy of the system. Wigner went on to discuss how
is a pseudo-differential operator with symbol defined by the potential energy of the system. Wigner went on to discuss how 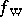 might be used to calculate quantities of physical interest. In particular, the density is
might be used to calculate quantities of physical interest. In particular, the density is 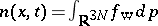 . Since, in general, the potential energy depends on the density, the Wigner equation is non-linear.
. Since, in general, the potential energy depends on the density, the Wigner equation is non-linear.
Generalizing to a mixed state, described not by a wave function but by a von Neumann density matrix [a2]
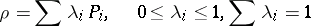 |
(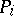 is the projection onto the vector
is the projection onto the vector 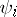 ):
):
 |
Generalizing further, let  be a (bounded) operator on
be a (bounded) operator on 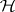 . Let
. Let  be a basis for
be a basis for 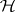 and write
and write 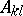 for
for 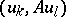 , where
, where 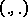 is the inner product in
is the inner product in  . Then the Wigner transform
. Then the Wigner transform 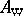 of the operator
of the operator 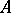 is
is
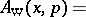 |
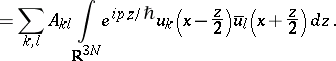 |
In particular, if 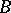 is a trace-class operator on
is a trace-class operator on 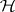 and
and 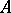 is bounded as above,
is bounded as above,
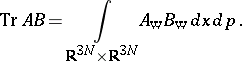 |
The Wigner transform of an operator is related to the Weyl transform [a3] of a phase-space function, introduced by H. Weyl in 1950 in an attempt to relate classical and quantum mechanics. Indeed, let 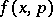 be an appropriate function in
be an appropriate function in 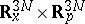 (see [a4] for a definition of "appropriate" ). Then the Weyl transform of
(see [a4] for a definition of "appropriate" ). Then the Weyl transform of  ,
,  , is defined in terms of the Fourier transform
, is defined in terms of the Fourier transform 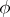 of
of 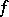 as [a5]
as [a5]
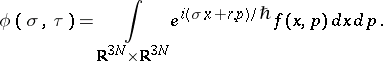 |
Here, 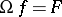 is the operator
is the operator
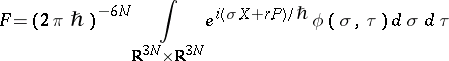 |
and  is the multiplication operator on
is the multiplication operator on  defined by
defined by 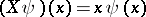 and
and 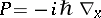 . These are the usual position and momentum operators of quantum mechanics [a2]. The Weyl and Wigner transforms are mutual inverses:
. These are the usual position and momentum operators of quantum mechanics [a2]. The Weyl and Wigner transforms are mutual inverses:  and
and 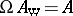 [a5].
[a5].
Serious mathematical interest in the Wigner transform revived in 1985, when H. Neunzert published [a6]. Since then, most mathematical attention has been paid to existence-uniqueness theory for the Wigner equation in 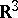 and, more recently, in a closed proper subset of
and, more recently, in a closed proper subset of  ,
, 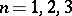 . While the situation in
. While the situation in 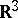 is pretty well understood, [a7], [a8] the more practical latter situation is still under study (1998), the main problem being the question of appropriate boundary conditions [a9].
is pretty well understood, [a7], [a8] the more practical latter situation is still under study (1998), the main problem being the question of appropriate boundary conditions [a9].
References
| [a1] | E. Wigner, "On the quantum correction for thermodynamic equilibrium" Phys. Rev. , 40 (1932) pp. 749–759 |
| [a2] | J. von Neumann, "Mathematical foundations of quantum mechanics" , Princeton Univ. Press (1955) |
| [a3] | H. Weyl, "The theory of groups and quantum mechanics" , Dover (1950) |
| [a4] | G.B. Folland, "Harmonic analysis in phase space" , Princeton Univ. Press (1989) |
| [a5] | P.F. Zweifel, "The Wigner transform and the Wigner–Poisson system" Trans. Theor. Stat. Phys. , 22 (1993) pp. 459–484 |
| [a6] | H. Neunzert, "The nuclear Vlasov equation: methods and results that can (not) be taken over from the "classical" case" Il Nuovo Cimento , 87A (1985) pp. 151–161 |
| [a7] | F. Brezzi, P. Markowich, "The three-dimensional Wigner–Poisson problem: existence, uniqueness and approximation" Math. Meth. Appl. Sci. , 14 (1991) pp. 35 |
| [a8] | R. Illner, H. Lange, P.F. Zweifel, "Global existence and asymptotic behaviour of solutions of the Wigner–Poisson and Schrödinger–Poisson systems" Math. Meth. Appl. Sci. , 17 (1994) pp. 349–376 |
| [a9] | P.F. Zweifel, B. Toomire, "Quantum transport theory" Trans. Theor. Stat. Phys. , 27 (1998) pp. 347–359 |
Wigner-Weyl transform. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Wigner-Weyl_transform&oldid=11631