Wiener process
A homogeneous Gaussian process 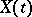 with independent increments. A Wiener process serves as one of the models of Brownian motion. A simple transformation will convert a Wiener process into the "standard" Wiener process
with independent increments. A Wiener process serves as one of the models of Brownian motion. A simple transformation will convert a Wiener process into the "standard" Wiener process 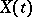 ,
, 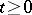 , for which
, for which
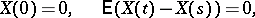 |
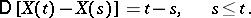 |
For these average values and incremental variances, this is the only almost-surely continuous process with independent increments. In what follows, the Wiener process will be understood to be this process.
The Wiener process 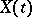 ,
, 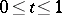 , can also be defined as the Gaussian process with zero expectation and covariance function
, can also be defined as the Gaussian process with zero expectation and covariance function
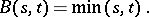 |
The Wiener process 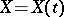 ,
,  , may also be defined as the homogeneous Markov process with transition function
, may also be defined as the homogeneous Markov process with transition function
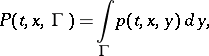 |
where the transition density 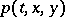 is the fundamental solution of the parabolic differential equation
is the fundamental solution of the parabolic differential equation
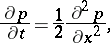 |
given by the formula
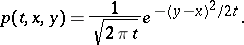 |
The transition function 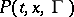 is invariant with respect to translations in the phase space:
is invariant with respect to translations in the phase space:
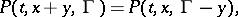 |
where 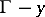 denotes the set
denotes the set 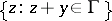 .
.
The Wiener process is the continuous analogue of the random walk of a particle which, at discrete moments of time  (multiples of
(multiples of 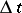 ), is randomly displaced by a quantity
), is randomly displaced by a quantity 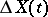 , independent of the past (
, independent of the past (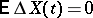 ,
, 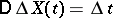 ); more precisely, if
); more precisely, if
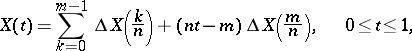 |
is the random trajectory of the motion of such a particle on the interval 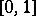 (where
(where 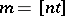 is the integer part of
is the integer part of 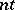 ,
, 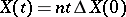 if
if 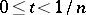 and
and 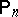 is the corresponding probability distribution in the space of continuous functions
is the corresponding probability distribution in the space of continuous functions 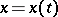 ,
, 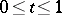 ), then the probability distribution
), then the probability distribution 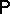 of the trajectory of the Wiener process
of the trajectory of the Wiener process 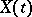 ,
, 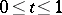 , is the limit (in the sense of weak convergence) of the distributions
, is the limit (in the sense of weak convergence) of the distributions 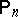 as
as 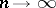 .
.
As a function with values in the Hilbert space 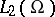 of all random variables
of all random variables 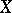 with
with 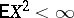 , in which the scalar product is defined by the formula
, in which the scalar product is defined by the formula
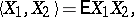 |
the Wiener process 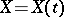 ,
, 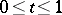 , may be canonically represented as follows:
, may be canonically represented as follows:
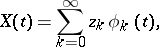 |
where 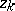 are independent Gaussian variables:
are independent Gaussian variables:
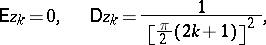 |
and
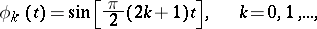 |
are the eigenfunctions of the operator 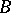 defined by the formula
defined by the formula
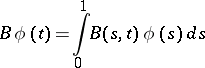 |
in the Hilbert space 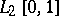 of all square-integrable (with respect to Lebesgue measure) functions
of all square-integrable (with respect to Lebesgue measure) functions 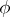 on
on 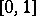 .
.
Almost-all trajectories of the Wiener process have the following properties:
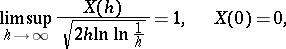 |
which is the law of the iterated logarithm;
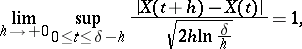 |
characterizing the modulus of continuity on 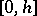 ; and
; and
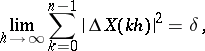 |
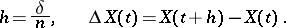 |
When applied to the Wiener process 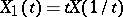 ,
, 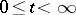 , the law of the iterated logarithm reads:
, the law of the iterated logarithm reads:
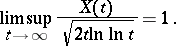 |
The distributions of the maximum 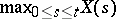 , of the time
, of the time 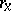 at which the Brownian particle first reaches a fixed point
at which the Brownian particle first reaches a fixed point 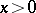 and of the location
and of the location  of the maximum
of the maximum 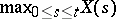 give insight in the nature of the movement of a Brownian particle; these distributions are given by the following formulas:
give insight in the nature of the movement of a Brownian particle; these distributions are given by the following formulas:
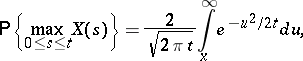 |
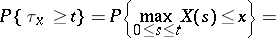 |
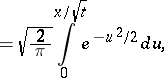 |
while the simultaneous density of the maximum 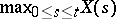 and its location
and its location  is given by:
is given by:
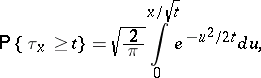 |
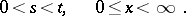 |
(The laws of the Wiener process remain unchanged on transforming the phase space 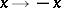 .) The joint distribution of the maximum point
.) The joint distribution of the maximum point  ,
, 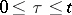 , and of the maximum
, and of the maximum 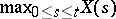 itself has the probability density
itself has the probability density
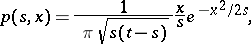 |
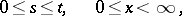 |
while the point  by itself (with probability one there is only one maximum on the interval
by itself (with probability one there is only one maximum on the interval 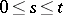 ) is distributed according to the arcsine law:
) is distributed according to the arcsine law:
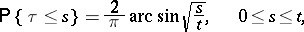 |
with the probability density:
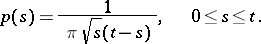 |
The following properties of the Wiener process are readily deduced from the formulas given above. The Brownian trajectory is nowhere differentiable; on starting from any point  this trajectory crosses the "level"
this trajectory crosses the "level"  (returns to its initial point) infinitely many times with probability one, however short the time
(returns to its initial point) infinitely many times with probability one, however short the time 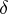 ; the Brownian trajectory passes through all points
; the Brownian trajectory passes through all points  (more precisely,
(more precisely, 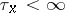 ) with probability one (the most probable value of
) with probability one (the most probable value of 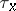 is of the order
is of the order 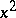 for large
for large  ); this trajectory, if considered on a fixed interval
); this trajectory, if considered on a fixed interval 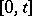 , tends to attain the extremal values near the end-points
, tends to attain the extremal values near the end-points 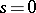 and
and  .
.
Since a Wiener process is a homogeneous Markov process, there exists an invariant measure 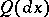 for it, namely:
for it, namely:
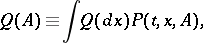 |
which, since the transition function 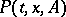 has been seen to be invariant, coincides with the Lebesgue measure on the real line:
has been seen to be invariant, coincides with the Lebesgue measure on the real line: 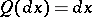 . The time
. The time 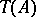 which a Brownian particle spends in
which a Brownian particle spends in  between the times 0 and
between the times 0 and 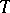 is such that
is such that
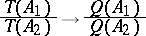 |
as 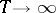 , with probability one for any bounded Borel sets
, with probability one for any bounded Borel sets 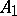 and
and 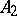 .
.
Wiener random fields, introduced by P. Lévy [3], are analogues of the Wiener process 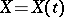 for a vector parameter
for a vector parameter 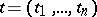 .
.
References
| [1] | K. Itô, H.P. McKean jr., "Diffusion processes and their sample paths" , Springer (1974) |
| [2] | Yu.V. [Yu.V. Prokhorov] Prohorov, Yu.A. Rozanov, "Probability theory, basic concepts. Limit theorems, random processes" , Springer (1969) (Translated from Russian) |
| [3] | P. Lévy, "Processus stochastiques et mouvement Brownien" , Gauthier-Villars (1965) |
| [4] | V.P. Pavlov, "Brownian motion" , Large Soviet Encyclopaedia , 4 (In Russian) |
Comments
The Wiener process is more commonly referred to as Brownian motion in the Western literature. It is by far the most important construct in stochastic analysis. See [a1]–[a3] for up-to-date accounts of its properties. Of particular importance is the theory of local time. The occupation time of a Borel set 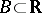 on the interval
on the interval 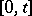 is:
is:
 |
There exists an almost-surely jointly-continuous random field 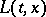 for
for 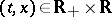 such that
such that
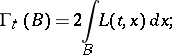 |
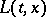 is the local time at
is the local time at  . For fixed
. For fixed 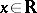 , sample paths of the process
, sample paths of the process 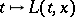 are increasing and continuous but singular with respect to Lebesgue measure.
are increasing and continuous but singular with respect to Lebesgue measure.
See also Markov process; Stochastic differential equation.
References
| [a1] | R. Durrett, "Brownian motion and martingales in analysis" , Wadsworth (1984) |
| [a2] | I. Karatzas, S.E. Shreve, "Brownian motion and stochastic calculus" , Springer (1988) |
| [a3] | D. Revuz, M. Yor, "Continuous martingales and Brownian motion" , Springer (1990) |
| [a4] | E.B. Dynkin, "Markov processes" , 1 , Springer (1965) (Translated from Russian) |
| [a5] | W. Feller, "An introduction to probability theory and its applications" , 1–2 , Wiley (1968–1971) |
| [a6] | I.I. [I.I. Gikhman] Gihman, A.V. [A.V. Skorokhod] Skorohod, "The theory of stochastic processes" , III , Springer (1975) (Translated from Russian) |
| [a7] | T. Hida, "Brownian motion" , Springer (1980) |
| [a8] | F. Spitzer, "Principles of random walk" , v. Nostrand (1964) |
| [a9] | J. Yeh, "Stochastic processes and the Wiener integral" , M. Dekker (1973) |
| [a10] | J.L. Doob, "Classical potential theory and its probabilistic counterpart" , Springer (1984) |
Wiener process. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Wiener_process&oldid=15877