Difference between revisions of "Wiener-Itô decomposition"
Ulf Rehmann (talk | contribs) m (moved Wiener-Ito decomposition to Wiener-Itô decomposition: accented title) |
m (Automatically changed introduction) |
||
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | ||
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. | ||
| + | |||
| + | Out of 115 formulas, 111 were replaced by TEX code.--> | ||
| + | |||
| + | {{TEX|semi-auto}}{{TEX|part}} | ||
''Itô–Wiener decomposition'' | ''Itô–Wiener decomposition'' | ||
An orthogonal decomposition of the [[Hilbert space|Hilbert space]] of square-integrable functions on a Gaussian space. It was first proved in 1938 by N. Wiener [[#References|[a6]]] in terms of homogeneous chaos (cf. also [[Wiener chaos decomposition|Wiener chaos decomposition]]). In 1951, K. Itô [[#References|[a1]]] defined multiple Wiener integrals to interpret homogeneous chaos and gave a different proof of the decomposition theorem. | An orthogonal decomposition of the [[Hilbert space|Hilbert space]] of square-integrable functions on a Gaussian space. It was first proved in 1938 by N. Wiener [[#References|[a6]]] in terms of homogeneous chaos (cf. also [[Wiener chaos decomposition|Wiener chaos decomposition]]). In 1951, K. Itô [[#References|[a1]]] defined multiple Wiener integrals to interpret homogeneous chaos and gave a different proof of the decomposition theorem. | ||
| − | Take an abstract Wiener space | + | Take an abstract Wiener space $( H , B )$ [[#References|[a3]]] (cf. also [[Wiener space, abstract|Wiener space, abstract]]). Let $\mu$ be the standard Gaussian measure on $B$. The abstract version of Wiener–Itô decomposition deals with a special orthogonal decomposition of the real Hilbert space $L ^ { 2 } ( \mu )$. |
| − | Each | + | Each $h \in H$ defines a normal [[Random variable|random variable]] $\tilde{h}$ on $B$ with mean $0$ and variance $| h | _ { H } ^ { 2 }$ [[#References|[a3]]]. Let $F _ { 0 } = \mathbf{R}$. For $n \geq 1$, let $F _ { n }$ be the $L ^ { 2 } ( \mu )$-closure of the linear space spanned by $1$ and random variables of the form $\tilde { h } _ { 1 } \ldots \tilde { h } _ { k }$ with $k \leq n$ and $h _ { j } \in H$ for $1 \leq j \leq k$. Then $\{ F _ { n } \} _ { n = 0 } ^ { \infty }$ is an increasing sequence of closed subspaces of $L ^ { 2 } ( \mu )$. Let $G _ { 0 } = \mathbf{R}$ and, for $n \geq 1$, let $G_n$ be the orthogonal complement of $F _ { n-1 } $ in $F _ { n }$. The elements in $G_n$ are called homogeneous chaos of degree $n$. Obviously, the spaces $G_n$ are orthogonal. Moreover, the Hilbert space $L ^ { 2 } ( \mu )$ is the direct sum of $G_n$ for $n \geq 0$, namely, $L ^ { 2 } ( \mu ) = \sum _ { n = 0 } ^ { \infty } G _ { n }$. |
| − | Fix | + | Fix $n \geq 1$. To describe $G_n$ more precisely, let $P_n$ be the orthogonal projection of $L ^ { 2 } ( \mu )$ onto the space $G_n$. For $h _ { 1 } \otimes \ldots \otimes h _ { n } \in H ^ { \otimes n }$, define |
| − | + | \begin{equation*} \theta _ { n } ( h _ { 1 } \bigotimes \ldots \bigotimes h _ { n } ) = P _ { n } ( \tilde { h _ { 1 } } \ldots \tilde { h _ { n } } ). \end{equation*} | |
| − | Then | + | Then $\theta _ { n } ( h _ { 1 } \otimes \ldots \otimes h _ { n } ) = \theta _ { n } ( h _ { 1 } \otimes^\wedge \ldots \otimes^\wedge \sim h _ { n } )$ (where $\otimes\hat{}$ denotes the symmetric [[Tensor product|tensor product]]) and |
| − | + | \begin{equation*} \left\| \theta _ { n } ( h _ { 1 } \bigotimes \ldots \bigotimes h _ { n } ) \right\| _ { L ^ { 2 } ( \mu ) } = \sqrt { n ! } \left| h _ { 1 } \widehat{\bigotimes} \ldots \widehat{\bigotimes} h _ { n } \right| _ { H ^{ \bigotimes n }}. \end{equation*} | |
| − | Thus, | + | Thus, $\theta _ { n }$ extends by continuity to a continuous [[Linear operator|linear operator]] from $H ^{\otimes n}$ into $G_n$ and is an [[Isometric mapping|isometric mapping]] (up to the constant $\sqrt { n ! }$) from $H ^ { \widehat{\otimes} n }$ into $G_n$. Actually, $\theta _ { n }$ is surjective and so for any $\varphi \in G _ { n }$, there exists a unique $f \in H ^ { \hat{\otimes} n }$ such that $\theta _ { n } ( f ) = \varphi$ and $\| \varphi \| _ { L ^ { 2 } ( \mu ) } = \sqrt { n ! } | f | _ { H ^ { \otimes n } }$. Therefore, for any $\varphi \in L ^ { 2 } ( \mu )$, there exists a unique sequence $\{ f _ { n } \} _ { n = 0 } ^ { \infty }$ with $f _ { n } \in H ^ { \widehat{ \otimes } n }$ such that |
| − | + | \begin{equation*} \varphi = \sum _ { n = 0 } ^ { \infty } \theta _ { n } ( f _ { n } ), \end{equation*} | |
| − | + | \begin{equation*} \| \varphi \| _ { L ^ { 2 } ( \mu ) } ^ { 2 } = \sum _ { n = 0 } ^ { \infty } n ! | f _ { n } | ^ { 2 } _ { H ^ {\bigotimes n}}. \end{equation*} | |
This is the abstract version of the Wiener–Itô decomposition theorem [[#References|[a2]]], [[#References|[a4]]], [[#References|[a5]]]. | This is the abstract version of the Wiener–Itô decomposition theorem [[#References|[a2]]], [[#References|[a4]]], [[#References|[a5]]]. | ||
| − | Let | + | Let $\Gamma ( H ) = \sum _ { n = 0 } ^ { \infty } H ^ { \widehat{\otimes} n }$. Define a [[Norm|norm]] on $\Gamma ( H )$ by |
| − | + | \begin{equation*} \| ( f _ { 0 } , f _ { 1 } , \ldots ) \| _ { \Gamma ( H ) } = \left( \sum _ { n = 0 } ^ { \infty } n ! |f _ { n } | _ { H^{\bigotimes n} } ^ { 2 } \right) ^ { 1 / 2 }. \end{equation*} | |
| − | The Hilbert space | + | The Hilbert space $\Gamma ( H )$ is called the Fock space of $H$ (cf. also [[Fock space|Fock space]]). The spaces $\Gamma ( H )$ and $L ^ { 2 } ( \mu )$ are isomorphic under the [[Unitary operator|unitary operator]] $\Theta$ defined by |
| − | + | \begin{equation*} \Theta ( f _ { 0 } , f _ { 1 } , \ldots ) = \sum _ { n = 0 } ^ { \infty } \theta _ { n } ( f _ { n } ). \end{equation*} | |
| − | Let | + | Let $\{ e _ { k } : k \geq 1 \}$ be an orthonormal basis (cf. also [[Orthogonal basis|Orthogonal basis]]) for $H$. For any non-negative integers $n _ { 1 } , n _ { 2 } , \dots$ such that $n _ { 1 } + n _ { 2 } + \ldots = n$, define |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130090/w13009072.png"/></td> </tr></table> |
| − | where | + | where $\mathcal{H} _ { k } ( x ) = ( - 1 ) ^ { n } e ^ { x ^ { 2 } / 2 } D _ { x } ^ { k } e ^ { - x ^ { 2 } / 2 }$ is the Hermite polynomial of degree $k$ (cf. also [[Hermite polynomials|Hermite polynomials]]). The set $\{ \varphi _ { n _ { 1 } , n _ { 2 } , \ldots } : n _ { j } \geq 0 , n _ { 1 } + n _ { 2 } + \ldots = n \}$ is an orthonormal basis for the space $G_n$ of homogeneous chaos of degree $n$. Hence the set $\{ \varphi _ { n _ { 1 } , n _ { 2 } , \ldots } : n _ { j } \geq 0 , n _ { 1 } + n _ { 2 } + \ldots = n , n \geq 0 \}$ forms an orthonormal basis for $L ^ { 2 } ( \mu )$. |
| − | Consider the classical Wiener space | + | Consider the classical Wiener space $( C ^ { \prime } , C )$ [[#References|[a3]]]. The Hilbert space $C ^ { \prime }$ is isomorphic to $L ^ { 2 } ( [ 0,1 ] )$ under the unitary operator $\iota( g ) = g ^ { \prime }$, $g \in C ^ { \prime }$. The standard Gaussian measure $\mu$ on $C$ is the Wiener measure and $B ( t , \omega ) = \omega ( t )$, $\omega \in C$, is a [[Brownian motion|Brownian motion]]. For $g \in L ^ { 2 } ( [ 0,1 ] )$, the random variable $\widetilde{( \iota ^ { - 1 } g )}$ is exactly the [[Wiener integral|Wiener integral]] $I ( g ) = \int _ { 0 } ^ { 1 } g ( t ) d B ( t )$. Let $g _ { j } \in L ^ { 2 } ( [ 0,1 ] )$, $1 \leq j \leq n$. The random variable |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130090/w13009094.png"/></td> </tr></table> |
| − | is a homogeneous chaos in the space | + | is a homogeneous chaos in the space $G_n$. The mapping $ { I } _ { n }$ extends by continuity to the space $L ^ { 2 } ( [ 0,1 ] ^ { n } )$. For $g \in L ^ { 2 } ( [ 0,1 ] ^ { n } )$, |
| − | + | \begin{equation*} I _ { n } ( g ) = \int _ { [ 0,1 ] ^ { n } } g ( t _ { 1 } , \ldots , t _ { n } ) d B ( t _ { 1 } ) \ldots d B ( t _ { n } ), \end{equation*} | |
| − | where the right-hand side is a multiple Wiener integral of order | + | where the right-hand side is a multiple Wiener integral of order $n$ as defined by Itô in [[#References|[a1]]] and $\| I _ { n } ( g ) \| _ { L ^{ 2} ( \mu ) } = \sqrt { n ! } | \hat{g} | _ { L ^{ 2} ( [ 0,1 ] ^ { n } )}$ (where $\hat{g}$ is the symmetrization of $g$.) For any $\varphi \in L ^ { 2 } ( \mu )$ there exists a unique sequence $\{ g _ { n } \} _ { n = 0 } ^ { \infty }$ of symmetric functions $g _ { n } \in L ^ { 2 } ( [ 0,1 ] ^ { n } )$ such that |
| − | + | \begin{equation*} \varphi = \sum _ { n = 0 } ^ { \infty } I _ { n } ( g _ { n } ), \end{equation*} | |
| − | + | \begin{equation*} \| \varphi \| _ { L ^ { 2 } ( \mu ) } ^ { 2 } = \sum _ { n = 0 } ^ { \infty } n ! | g _ { n } | _ { L^2 ( [ 0,1 ] ^ { n } ) } ^ { 2 } . \end{equation*} | |
| − | This is the Wiener–Itô decomposition theorem in terms of multiple Wiener integrals. An orthonormal basis for | + | This is the Wiener–Itô decomposition theorem in terms of multiple Wiener integrals. An orthonormal basis for $L ^ { 2 } ( \mu )$ is given by the set |
| − | + | \begin{equation*} \frac { 1 } { \sqrt { n _ { 1 } ! n _ { 2 } ! \ldots } }. \end{equation*} | |
| − | + | \begin{equation*} .\mathcal{H} _ { n _ { 1 } } \left( \int _ { 0 } ^ { 1 } e _ { 1 } ( t ) d B ( t ) \right) \mathcal{H} _ { n _ { 2 } } \left( \int _ { 0 } ^ { 1 } e _ { 2 } ( t ) d B ( t ) \right) \ldots ,\; n _ { j } \geq 0 ,\; n _ { 1 } + n _ { 2 } + \ldots = n ,\; n \geq 0, \end{equation*} | |
| − | where | + | where $\{ e _ { k } : k \geq 1 \}$ is an orthonormal basis for $L ^ { 2 } ( [ 0,1 ] )$ and the integrals are Wiener integrals. |
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> K. Itô, "Multiple Wiener integral" ''J. Math. Soc. Japan'' , '''3''' (1951) pp. 157–169</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> G. Kallianpur, "Stochastic filtering theory" , Springer (1980)</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> H.-H. Kuo, "Gaussian measures in Banach spaces" , ''Lecture Notes in Mathematics'' , '''463''' , Springer (1975)</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> H.-H. Kuo, "White noise distribution theory" , CRC (1996)</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> N. Obata, "White noise calculus and Fock space" , ''Lecture Notes in Mathematics'' , '''1577''' , Springer (1994)</td></tr><tr><td valign="top">[a6]</td> <td valign="top"> N. Wiener, "The homogeneous chaos" ''Amer. J. Math.'' , '''60''' (1938) pp. 897–936</td></tr></table> |
Latest revision as of 17:43, 1 July 2020
Itô–Wiener decomposition
An orthogonal decomposition of the Hilbert space of square-integrable functions on a Gaussian space. It was first proved in 1938 by N. Wiener [a6] in terms of homogeneous chaos (cf. also Wiener chaos decomposition). In 1951, K. Itô [a1] defined multiple Wiener integrals to interpret homogeneous chaos and gave a different proof of the decomposition theorem.
Take an abstract Wiener space $( H , B )$ [a3] (cf. also Wiener space, abstract). Let $\mu$ be the standard Gaussian measure on $B$. The abstract version of Wiener–Itô decomposition deals with a special orthogonal decomposition of the real Hilbert space $L ^ { 2 } ( \mu )$.
Each $h \in H$ defines a normal random variable $\tilde{h}$ on $B$ with mean $0$ and variance $| h | _ { H } ^ { 2 }$ [a3]. Let $F _ { 0 } = \mathbf{R}$. For $n \geq 1$, let $F _ { n }$ be the $L ^ { 2 } ( \mu )$-closure of the linear space spanned by $1$ and random variables of the form $\tilde { h } _ { 1 } \ldots \tilde { h } _ { k }$ with $k \leq n$ and $h _ { j } \in H$ for $1 \leq j \leq k$. Then $\{ F _ { n } \} _ { n = 0 } ^ { \infty }$ is an increasing sequence of closed subspaces of $L ^ { 2 } ( \mu )$. Let $G _ { 0 } = \mathbf{R}$ and, for $n \geq 1$, let $G_n$ be the orthogonal complement of $F _ { n-1 } $ in $F _ { n }$. The elements in $G_n$ are called homogeneous chaos of degree $n$. Obviously, the spaces $G_n$ are orthogonal. Moreover, the Hilbert space $L ^ { 2 } ( \mu )$ is the direct sum of $G_n$ for $n \geq 0$, namely, $L ^ { 2 } ( \mu ) = \sum _ { n = 0 } ^ { \infty } G _ { n }$.
Fix $n \geq 1$. To describe $G_n$ more precisely, let $P_n$ be the orthogonal projection of $L ^ { 2 } ( \mu )$ onto the space $G_n$. For $h _ { 1 } \otimes \ldots \otimes h _ { n } \in H ^ { \otimes n }$, define
\begin{equation*} \theta _ { n } ( h _ { 1 } \bigotimes \ldots \bigotimes h _ { n } ) = P _ { n } ( \tilde { h _ { 1 } } \ldots \tilde { h _ { n } } ). \end{equation*}
Then $\theta _ { n } ( h _ { 1 } \otimes \ldots \otimes h _ { n } ) = \theta _ { n } ( h _ { 1 } \otimes^\wedge \ldots \otimes^\wedge \sim h _ { n } )$ (where $\otimes\hat{}$ denotes the symmetric tensor product) and
\begin{equation*} \left\| \theta _ { n } ( h _ { 1 } \bigotimes \ldots \bigotimes h _ { n } ) \right\| _ { L ^ { 2 } ( \mu ) } = \sqrt { n ! } \left| h _ { 1 } \widehat{\bigotimes} \ldots \widehat{\bigotimes} h _ { n } \right| _ { H ^{ \bigotimes n }}. \end{equation*}
Thus, $\theta _ { n }$ extends by continuity to a continuous linear operator from $H ^{\otimes n}$ into $G_n$ and is an isometric mapping (up to the constant $\sqrt { n ! }$) from $H ^ { \widehat{\otimes} n }$ into $G_n$. Actually, $\theta _ { n }$ is surjective and so for any $\varphi \in G _ { n }$, there exists a unique $f \in H ^ { \hat{\otimes} n }$ such that $\theta _ { n } ( f ) = \varphi$ and $\| \varphi \| _ { L ^ { 2 } ( \mu ) } = \sqrt { n ! } | f | _ { H ^ { \otimes n } }$. Therefore, for any $\varphi \in L ^ { 2 } ( \mu )$, there exists a unique sequence $\{ f _ { n } \} _ { n = 0 } ^ { \infty }$ with $f _ { n } \in H ^ { \widehat{ \otimes } n }$ such that
\begin{equation*} \varphi = \sum _ { n = 0 } ^ { \infty } \theta _ { n } ( f _ { n } ), \end{equation*}
\begin{equation*} \| \varphi \| _ { L ^ { 2 } ( \mu ) } ^ { 2 } = \sum _ { n = 0 } ^ { \infty } n ! | f _ { n } | ^ { 2 } _ { H ^ {\bigotimes n}}. \end{equation*}
This is the abstract version of the Wiener–Itô decomposition theorem [a2], [a4], [a5].
Let $\Gamma ( H ) = \sum _ { n = 0 } ^ { \infty } H ^ { \widehat{\otimes} n }$. Define a norm on $\Gamma ( H )$ by
\begin{equation*} \| ( f _ { 0 } , f _ { 1 } , \ldots ) \| _ { \Gamma ( H ) } = \left( \sum _ { n = 0 } ^ { \infty } n ! |f _ { n } | _ { H^{\bigotimes n} } ^ { 2 } \right) ^ { 1 / 2 }. \end{equation*}
The Hilbert space $\Gamma ( H )$ is called the Fock space of $H$ (cf. also Fock space). The spaces $\Gamma ( H )$ and $L ^ { 2 } ( \mu )$ are isomorphic under the unitary operator $\Theta$ defined by
\begin{equation*} \Theta ( f _ { 0 } , f _ { 1 } , \ldots ) = \sum _ { n = 0 } ^ { \infty } \theta _ { n } ( f _ { n } ). \end{equation*}
Let $\{ e _ { k } : k \geq 1 \}$ be an orthonormal basis (cf. also Orthogonal basis) for $H$. For any non-negative integers $n _ { 1 } , n _ { 2 } , \dots$ such that $n _ { 1 } + n _ { 2 } + \ldots = n$, define
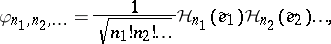 |
where $\mathcal{H} _ { k } ( x ) = ( - 1 ) ^ { n } e ^ { x ^ { 2 } / 2 } D _ { x } ^ { k } e ^ { - x ^ { 2 } / 2 }$ is the Hermite polynomial of degree $k$ (cf. also Hermite polynomials). The set $\{ \varphi _ { n _ { 1 } , n _ { 2 } , \ldots } : n _ { j } \geq 0 , n _ { 1 } + n _ { 2 } + \ldots = n \}$ is an orthonormal basis for the space $G_n$ of homogeneous chaos of degree $n$. Hence the set $\{ \varphi _ { n _ { 1 } , n _ { 2 } , \ldots } : n _ { j } \geq 0 , n _ { 1 } + n _ { 2 } + \ldots = n , n \geq 0 \}$ forms an orthonormal basis for $L ^ { 2 } ( \mu )$.
Consider the classical Wiener space $( C ^ { \prime } , C )$ [a3]. The Hilbert space $C ^ { \prime }$ is isomorphic to $L ^ { 2 } ( [ 0,1 ] )$ under the unitary operator $\iota( g ) = g ^ { \prime }$, $g \in C ^ { \prime }$. The standard Gaussian measure $\mu$ on $C$ is the Wiener measure and $B ( t , \omega ) = \omega ( t )$, $\omega \in C$, is a Brownian motion. For $g \in L ^ { 2 } ( [ 0,1 ] )$, the random variable $\widetilde{( \iota ^ { - 1 } g )}$ is exactly the Wiener integral $I ( g ) = \int _ { 0 } ^ { 1 } g ( t ) d B ( t )$. Let $g _ { j } \in L ^ { 2 } ( [ 0,1 ] )$, $1 \leq j \leq n$. The random variable
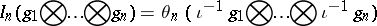 |
is a homogeneous chaos in the space $G_n$. The mapping $ { I } _ { n }$ extends by continuity to the space $L ^ { 2 } ( [ 0,1 ] ^ { n } )$. For $g \in L ^ { 2 } ( [ 0,1 ] ^ { n } )$,
\begin{equation*} I _ { n } ( g ) = \int _ { [ 0,1 ] ^ { n } } g ( t _ { 1 } , \ldots , t _ { n } ) d B ( t _ { 1 } ) \ldots d B ( t _ { n } ), \end{equation*}
where the right-hand side is a multiple Wiener integral of order $n$ as defined by Itô in [a1] and $\| I _ { n } ( g ) \| _ { L ^{ 2} ( \mu ) } = \sqrt { n ! } | \hat{g} | _ { L ^{ 2} ( [ 0,1 ] ^ { n } )}$ (where $\hat{g}$ is the symmetrization of $g$.) For any $\varphi \in L ^ { 2 } ( \mu )$ there exists a unique sequence $\{ g _ { n } \} _ { n = 0 } ^ { \infty }$ of symmetric functions $g _ { n } \in L ^ { 2 } ( [ 0,1 ] ^ { n } )$ such that
\begin{equation*} \varphi = \sum _ { n = 0 } ^ { \infty } I _ { n } ( g _ { n } ), \end{equation*}
\begin{equation*} \| \varphi \| _ { L ^ { 2 } ( \mu ) } ^ { 2 } = \sum _ { n = 0 } ^ { \infty } n ! | g _ { n } | _ { L^2 ( [ 0,1 ] ^ { n } ) } ^ { 2 } . \end{equation*}
This is the Wiener–Itô decomposition theorem in terms of multiple Wiener integrals. An orthonormal basis for $L ^ { 2 } ( \mu )$ is given by the set
\begin{equation*} \frac { 1 } { \sqrt { n _ { 1 } ! n _ { 2 } ! \ldots } }. \end{equation*}
\begin{equation*} .\mathcal{H} _ { n _ { 1 } } \left( \int _ { 0 } ^ { 1 } e _ { 1 } ( t ) d B ( t ) \right) \mathcal{H} _ { n _ { 2 } } \left( \int _ { 0 } ^ { 1 } e _ { 2 } ( t ) d B ( t ) \right) \ldots ,\; n _ { j } \geq 0 ,\; n _ { 1 } + n _ { 2 } + \ldots = n ,\; n \geq 0, \end{equation*}
where $\{ e _ { k } : k \geq 1 \}$ is an orthonormal basis for $L ^ { 2 } ( [ 0,1 ] )$ and the integrals are Wiener integrals.
References
| [a1] | K. Itô, "Multiple Wiener integral" J. Math. Soc. Japan , 3 (1951) pp. 157–169 |
| [a2] | G. Kallianpur, "Stochastic filtering theory" , Springer (1980) |
| [a3] | H.-H. Kuo, "Gaussian measures in Banach spaces" , Lecture Notes in Mathematics , 463 , Springer (1975) |
| [a4] | H.-H. Kuo, "White noise distribution theory" , CRC (1996) |
| [a5] | N. Obata, "White noise calculus and Fock space" , Lecture Notes in Mathematics , 1577 , Springer (1994) |
| [a6] | N. Wiener, "The homogeneous chaos" Amer. J. Math. , 60 (1938) pp. 897–936 |
Wiener-Itô decomposition. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Wiener-It%C3%B4_decomposition&oldid=23558