Wiener-Hopf operator
An operator which arises from another operator by compression to a subspace. Given a linear operator  and a projection
and a projection  on
on  with range
with range  , the corresponding Wiener–Hopf operator
, the corresponding Wiener–Hopf operator  is defined as the operator on
is defined as the operator on  that sends
that sends  to
to  . Thus,
. Thus,  .
.
A Wiener–Hopf integral operator formally acts by the rule
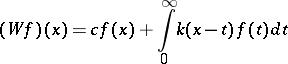 |
(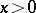 ) on some space of functions over
) on some space of functions over 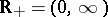 , say on
, say on 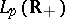 (
(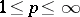 ). It may be regarded as the restriction to
). It may be regarded as the restriction to 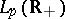 of a convolution integral operator on
of a convolution integral operator on 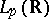 . The operator
. The operator 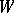 is bounded if, for example,
is bounded if, for example, 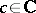 and
and 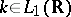 . Many properties of
. Many properties of  can be read off from its symbol. This is the function
can be read off from its symbol. This is the function  given by
given by
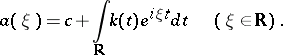 |
The operator 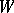 is Fredholm (cf. Fredholm operator), i.e. invertible modulo compact operators, if and only if its symbol
is Fredholm (cf. Fredholm operator), i.e. invertible modulo compact operators, if and only if its symbol  has no zeros on the one-point compactification
has no zeros on the one-point compactification 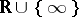 (cf. also Aleksandrov compactification) of
(cf. also Aleksandrov compactification) of 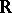 . In that case the kernel and cokernel dimensions of
. In that case the kernel and cokernel dimensions of 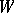 are:
are:
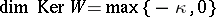 |
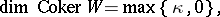 |
where 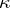 is the winding number of the symbol
is the winding number of the symbol  about the origin. The equation
about the origin. The equation 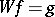 can be solved by Wiener–Hopf factorization, which means that one represents
can be solved by Wiener–Hopf factorization, which means that one represents  in the form
in the form
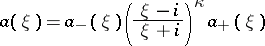 |
such that 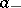 and
and 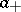 extend to analytic functions without zeros in the lower and upper complex half-planes, respectively.
extend to analytic functions without zeros in the lower and upper complex half-planes, respectively.
Many interesting operators are Wiener–Hopf integral operators with discontinuous symbols. For example, the Cauchy singular integral operator 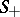 (cf. also Singular integral) on
(cf. also Singular integral) on 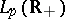 (
(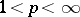 ),
),
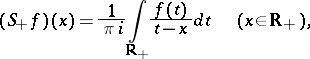 |
can be interpreted as the Wiener–Hopf integral operator with symbol 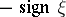 . The spectrum of
. The spectrum of 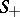 on
on 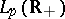 is the set of all
is the set of all 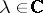 at which the line segment
at which the line segment 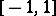 is seen at an angle of at least
is seen at an angle of at least 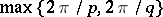 , where
, where 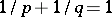 .
.
Wiener–Hopf integral operators with matrix-valued symbols, on finite intervals, or on higher-dimensional domains (including the quarter-plane) have also been extensively studied.
A discrete Wiener–Hopf operator, or a Toeplitz operator (cf. also Toeplitz matrix), is given by a matrix of the form 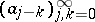 on some sequence space, e.g. on
on some sequence space, e.g. on 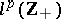 . In this case the symbol is the function on the complex unit circle whose Fourier coefficients constitute the sequence
. In this case the symbol is the function on the complex unit circle whose Fourier coefficients constitute the sequence 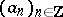 .
.
There is a rich literature on Wiener–Hopf operators. A good introduction is the classical monograph [a1]; [a2] and [a3] provide an overview of some recent developments.
References
| [a1] | I. Gohberg, I.A. Feldman, "Convolution equations and projection methods for their solution" , Amer. Math. Soc. (1974) |
| [a2] | A. Böttcher, B. Silbermann, "Analysis of Toeplitz operators" , Springer (1990) |
| [a3] | I. Gohberg, S. Goldberg, M.A. Kaashoek, "Classes of linear operators" , I–II , Birkhäuser (1990–1993) |
Wiener-Hopf operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Wiener-Hopf_operator&oldid=16439