Whittaker equation
From Encyclopedia of Mathematics
A linear homogeneous ordinary differential equation of the second order:
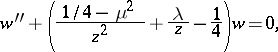 | (*) |
where the variables 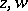 and the parameters
and the parameters 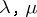 may take arbitrary complex values. Equation (*) represents the reduced form of a degenerate hypergeometric equation and was first studied by E.T. Whittaker [1]. For
may take arbitrary complex values. Equation (*) represents the reduced form of a degenerate hypergeometric equation and was first studied by E.T. Whittaker [1]. For 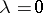 the Whittaker equation is equivalent to the Bessel equation. If
the Whittaker equation is equivalent to the Bessel equation. If 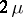 is not an integer, a fundamental system of solutions of the Whittaker equation consists of the functions
is not an integer, a fundamental system of solutions of the Whittaker equation consists of the functions 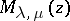 and
and  ; here
; here 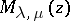 is the Whittaker function (cf. Whittaker functions). For any value of the parameters the general solution of the Whittaker equation may be written in the form of a linear combination
is the Whittaker function (cf. Whittaker functions). For any value of the parameters the general solution of the Whittaker equation may be written in the form of a linear combination
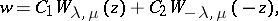 |
where 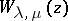 is the Whittaker function.
is the Whittaker function.
References
| [1] | E.T. Whittaker, "An expression of certain known functions as generalized hypergeometric functions" Bull. Amer. Math. Soc. , 10 (1903) pp. 125–134 |
| [2] | E.T. Whittaker, G.N. Watson, "A course of modern analysis" , Cambridge Univ. Press (1952) |
| [3] | H. Bateman (ed.) A. Erdélyi (ed.) , Higher transcendental functions , 1. The gamma function. The hypergeometric functions. Legendre functions , McGraw-Hill (1953) |
| [4] | A. Kratzer, W. Franz, "Transzendente Funktionen" , Akad. Verlagsgesell. Geest u. Portig K.-D. (1960) |
| [5] | E. Kamke, "Differentialgleichungen: Lösungen und Lösungsmethoden" , 1. Gewöhnliche Differentialgleichungen , Akad. Verlagsgesell. (1942) |
How to Cite This Entry:
Whittaker equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Whittaker_equation&oldid=12547
Whittaker equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Whittaker_equation&oldid=12547
This article was adapted from an original article by N.Kh. Rozov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article