Whitehead test module
Let 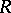 be an associative ring with unit and let
be an associative ring with unit and let 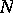 be a (unitary right
be a (unitary right 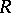 -) module (cf. also Associative rings and algebras; Module). Then
-) module (cf. also Associative rings and algebras; Module). Then 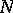 is a Whitehead test module for projectivity (or a p-test module) if for each module
is a Whitehead test module for projectivity (or a p-test module) if for each module 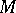 ,
, 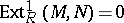 implies
implies  is projective (cf. also Projective module). Dually,
is projective (cf. also Projective module). Dually, 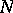 is a Whitehead test module for injectivity (or an i-test module) if for each module
is a Whitehead test module for injectivity (or an i-test module) if for each module 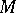 ,
, 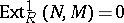 implies
implies 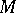 is injective (cf. also Injective module). So, Whitehead test modules make it possible to test for projectivity (injectivity) of a module by computing a single
is injective (cf. also Injective module). So, Whitehead test modules make it possible to test for projectivity (injectivity) of a module by computing a single 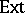 -group.
-group.
By Baer's criterion, for any ring 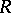 there is a proper class of i-test modules. Dually, for any right-perfect ring (cf. also Perfect ring) there is a proper class of p-test modules. If
there is a proper class of i-test modules. Dually, for any right-perfect ring (cf. also Perfect ring) there is a proper class of p-test modules. If 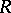 is not right perfect, then it is consistent with ZFC (cf. Set theory; Zermelo axiom) that there are no p-test modules, [a2], [a8].
is not right perfect, then it is consistent with ZFC (cf. Set theory; Zermelo axiom) that there are no p-test modules, [a2], [a8].
This is related to the structure of Whitehead modules (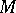 is a Whitehead module if
is a Whitehead module if 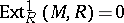 , [a1]). If
, [a1]). If 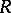 is a right-hereditary ring, then there is a cyclic p-test module if and only if
is a right-hereditary ring, then there is a cyclic p-test module if and only if 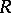 is p-test if and only if every Whitehead module is projective. The validity of the latter for
is p-test if and only if every Whitehead module is projective. The validity of the latter for 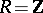 is the famous Whitehead problem, whose independence of ZFC was proved by S. Shelah [a5], [a6], and whose combinatorial equivalent was identified in [a3]. If
is the famous Whitehead problem, whose independence of ZFC was proved by S. Shelah [a5], [a6], and whose combinatorial equivalent was identified in [a3]. If 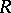 is right hereditary but not right perfect, then it is consistent with ZFC that there is a proper class of p-test modules [a8].
is right hereditary but not right perfect, then it is consistent with ZFC that there is a proper class of p-test modules [a8].
Let 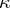 be a cardinal number. Then
be a cardinal number. Then 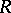 is
is 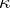 -saturated if each non-projective
-saturated if each non-projective 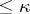 -generated module is an i-test module. If
-generated module is an i-test module. If 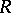 is
is 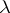 -saturated for all cardinal numbers
-saturated for all cardinal numbers  , then
, then 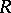 is called a fully saturated ring [a7]. There exist various non-Artinian
is called a fully saturated ring [a7]. There exist various non-Artinian  -saturated rings for
-saturated rings for 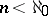 , but all
, but all 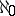 -saturated rings are Artinian (cf. also Artinian ring). Moreover, all right-hereditary
-saturated rings are Artinian (cf. also Artinian ring). Moreover, all right-hereditary 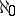 -saturated rings are fully saturated, and their class coincides with the class of rings
-saturated rings are fully saturated, and their class coincides with the class of rings 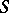 ,
, 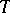 , or
, or 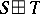 , where
, where 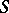 is completely reducible and
is completely reducible and 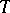 is Morita equivalent (cf. Morita equivalence) to the upper triangular
is Morita equivalent (cf. Morita equivalence) to the upper triangular 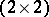 -matrix ring over a skew-field [a4] (cf. also Matrix ring; Ring with division; Division algebra)
-matrix ring over a skew-field [a4] (cf. also Matrix ring; Ring with division; Division algebra)
References
| [a1] | P.C. Eklof, A.H. Mekler, "Almost free modules: set-theoretic methods" , North-Holland (1990) |
| [a2] | P.C. Eklof, S. Shelah, "On Whitehead modules" J. Algebra , 142 (1991) pp. 492–510 |
| [a3] | P.C. Eklof, S. Shelah, "A combinatorial principle equivalent to the existence of non-free Whitehead groups" Contemp. Math. , 171 (1994) pp. 79–98 |
| [a4] | P.C. Eklof, J. Trlifaj, "How to make Ext vanish" preprint |
| [a5] | S. Shelah, "Infinite abelian groups, Whitehead problem and some constructions" Israel J. Math. , 18 (1974) pp. 243–256 |
| [a6] | S. Shelah, "A compactness theorem for singular cardinals, free algebras, Whitehead problem and transversals" Israel J. Math. , 21 (1975) pp. 319–349 |
| [a7] | J. Trlifaj, "Associative rings and the Whitehead property of modules" , Algebra Berichte , 63 , R. Fischer (1990) |
| [a8] | J. Trlifaj, "Whitehead test modules" Trans. Amer. Math. Soc. , 348 (1996) pp. 1521–1554 |
Whitehead test module. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Whitehead_test_module&oldid=16198