Whitehead problem
A problem attributed, to J.H.C. Whitehead, which asks for a characterization of Abelian groups  that satisfy the homological condition
that satisfy the homological condition  , where
, where  is the group of integers under addition (cf. also Homology). A group which satisfies this condition is called a Whitehead group. An equivalent characterization is:
is the group of integers under addition (cf. also Homology). A group which satisfies this condition is called a Whitehead group. An equivalent characterization is:  is a Whitehead group if and only if for every surjective homomorphism
is a Whitehead group if and only if for every surjective homomorphism  onto
onto  , if the kernel of
, if the kernel of  is isomorphic to
is isomorphic to  , then the kernel is a direct summand of the domain of
, then the kernel is a direct summand of the domain of  . A sufficient condition for
. A sufficient condition for 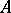 to be a Whitehead group is that
to be a Whitehead group is that 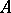 is free (see Free Abelian group). This condition has been proved to be necessary if
is free (see Free Abelian group). This condition has been proved to be necessary if 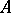 is countable. Since a subgroup of a Whitehead group is again a Whitehead group, this means that every Whitehead group is
is countable. Since a subgroup of a Whitehead group is again a Whitehead group, this means that every Whitehead group is 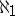 -free, that is, every countable subgroup is free. Before 1973 only partial results were obtained for uncountable groups: Whitehead groups were proved to be separable and slender, and under the assumption of the continuum hypothesis (
-free, that is, every countable subgroup is free. Before 1973 only partial results were obtained for uncountable groups: Whitehead groups were proved to be separable and slender, and under the assumption of the continuum hypothesis (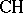 ), they were proved to be strongly
), they were proved to be strongly 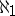 -free, that is, every countable subset is contained in a countable free subgroup which is a direct summand of countable subgroups containing it (see [a3] for results prior to 1973).
-free, that is, every countable subset is contained in a countable free subgroup which is a direct summand of countable subgroups containing it (see [a3] for results prior to 1973).
In 1973, S. Shelah [a5] proved that it is undecidable under the axioms of Zermelo–Frankel set theory (cf. also Set theory), ZFC, whether every Whitehead group of cardinality 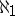 is free. Specifically, he proved that this is true assuming the Gödel constructibility axiom,
is free. Specifically, he proved that this is true assuming the Gödel constructibility axiom, 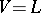 (see Gödel constructive set), but it is false assuming Martin's axiom (cf. Suslin hypothesis) and the negation of the continuum hypothesis (
(see Gödel constructive set), but it is false assuming Martin's axiom (cf. Suslin hypothesis) and the negation of the continuum hypothesis (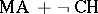 ). Later he proved that
). Later he proved that 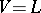 implies that every Whitehead group, of arbitrary cardinality, is free [a6]. He also proved that the problem is undecidable even if
implies that every Whitehead group, of arbitrary cardinality, is free [a6]. He also proved that the problem is undecidable even if 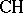 is assumed [a7] and that it is consistent with
is assumed [a7] and that it is consistent with 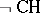 that there are Whitehead groups of cardinality
that there are Whitehead groups of cardinality 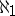 that are not strongly
that are not strongly 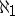 -free [a8].
-free [a8].
For more information see [a1], [a4] or [a2].
References
| [a1] | P.C. Eklof, "Whitehead's problem is undecidable" Amer. Math. Monthly , 83 (1976) pp. 775–788 |
| [a2] | P.C. Eklof, A.H. Mekler, "Almost free modules" , North-Holland (1990) |
| [a3] | L. Fuchs, "Infinite Abelian groups" , 2 , Acad. Press (1973) |
| [a4] | R. J. Nunke, "Whitehead's problem" , Abelian Group Theory , Lecture Notes in Mathematics , 616 , Springer (1977) pp. 240–250 |
| [a5] | S. Shelah, "Infinite abelian groups, Whitehead problem and some constructions" Israel J. Math. , 18 (1974) pp. 243–25 |
| [a6] | S. Shelah, "A compactness theorem for singular cardinals, free algebras, Whitehead problem and transversals" Israel J. Math. , 21 (1975) pp. 319–349 |
| [a7] | S. Shelah, "Whitehead groups may not be free even assuming CH, I" Israel J. Math. , 28 (1977) pp. 193–203 |
| [a8] | S. Shelah, "On uncountable abelian groups" Israel J. Math. , 32 (1979) pp. 311–330 |
| [a9] | S. Shelah, "Whitehead groups may not be free even assuming CH, II" Israel J. Math. , 35 (1980) pp. 257–285 |
Whitehead problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Whitehead_problem&oldid=17939