Weyl theorem
on operator perturbation
The spectrum  of a (possibly unbounded) self-adjoint operator
of a (possibly unbounded) self-adjoint operator 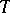 is naturally divided into a point spectrum
is naturally divided into a point spectrum 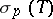 (i.e., the set of eigenvalues) and a continuous spectrum
(i.e., the set of eigenvalues) and a continuous spectrum 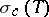 , both subsets of the real axis (cf. also Spectrum of an operator). The continuous spectrum is very sensitive against perturbations. The Weyl–von Neumann theorem [a2], Sect. X.2.2, states that for any self-adjoint operator
, both subsets of the real axis (cf. also Spectrum of an operator). The continuous spectrum is very sensitive against perturbations. The Weyl–von Neumann theorem [a2], Sect. X.2.2, states that for any self-adjoint operator 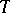 in a separable Hilbert space there exists a (compact) self-adjoint operator
in a separable Hilbert space there exists a (compact) self-adjoint operator 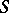 in the Hilbert–Schmidt class (cf. also Hilbert–Schmidt operator) such that
in the Hilbert–Schmidt class (cf. also Hilbert–Schmidt operator) such that 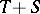 has a pure point spectrum. Moreover,
has a pure point spectrum. Moreover, 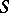 can be chosen arbitrarily small in the Hilbert–Schmidt norm. The set of eigenvalues obtained by perturbation of a continuous spectrum is dense in any interval covered by the continuous spectrum of the unperturbed operator. In spectral theory one introduces therefore another subset of
can be chosen arbitrarily small in the Hilbert–Schmidt norm. The set of eigenvalues obtained by perturbation of a continuous spectrum is dense in any interval covered by the continuous spectrum of the unperturbed operator. In spectral theory one introduces therefore another subset of 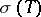 which is more stable under perturbations. The essential spectrum
which is more stable under perturbations. The essential spectrum  is defined as
is defined as 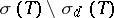 , where
, where 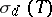 is the set of all isolated eigenvalues with finite multiplicity. H. Weyl proved (in a special case) the following result [a4], which is now commonly known as Weyl's theorem: Let
is the set of all isolated eigenvalues with finite multiplicity. H. Weyl proved (in a special case) the following result [a4], which is now commonly known as Weyl's theorem: Let 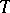 be self-adjoint and
be self-adjoint and 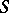 symmetric and compact. Then
symmetric and compact. Then
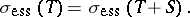 |
In fact, it is even sufficient to require the relative compactness of 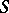 , which means that the operator
, which means that the operator 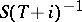 is compact. Another variant of the Weyl theorem states that two self-adjoint operators
is compact. Another variant of the Weyl theorem states that two self-adjoint operators 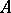 and
and 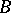 have the same essential spectrum if the difference of the resolvents
have the same essential spectrum if the difference of the resolvents 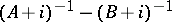 is compact [a3] (cf. also Resolvent). The Weyl theorem is very important in mathematical quantum mechanics, where it serves to prove that
is compact [a3] (cf. also Resolvent). The Weyl theorem is very important in mathematical quantum mechanics, where it serves to prove that 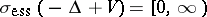 for a large class of two-body potentials. (A generalization to the
for a large class of two-body potentials. (A generalization to the 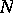 -body problem is the HVZ theorem by W. Hunziker, C. van Winter, and G. Zhislin, see [a3].) The situation is considerably more complicated for non-self-adjoint operators, where there are several possible definitions of the essential spectrum [a1]. In general, one defines the Weyl spectrum as the largest subset of the spectrum that is invariant under compact perturbations.
-body problem is the HVZ theorem by W. Hunziker, C. van Winter, and G. Zhislin, see [a3].) The situation is considerably more complicated for non-self-adjoint operators, where there are several possible definitions of the essential spectrum [a1]. In general, one defines the Weyl spectrum as the largest subset of the spectrum that is invariant under compact perturbations.
References
| [a1] | K. Gustafson, "Necessary and sufficient conditions for Weyl's theorem" Michigan Math. J. , 19 (1972) pp. 71–81 |
| [a2] | T. Kato, "Perturbation theory for linear operators" , Springer (1976) |
| [a3] | M. Reed, B. Simon, "Methods in modern mathematical physics IV. Analysis of operators" , Acad. Press (1978) |
| [a4] | H. Weyl, "Über quadratische Formen, deren Differenz vollstetig ist" Rend. Circ. Mat. Palermo , 27 (1909) pp. 373–392 |
Weyl theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weyl_theorem&oldid=16328