Difference between revisions of "Weyl tensor"
m (AUTOMATIC EDIT (latexlist): Replaced 70 formulas out of 81 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
m (Automatically changed introduction) |
||
| Line 2: | Line 2: | ||
the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
was used. | was used. | ||
| − | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. |
Out of 81 formulas, 70 were replaced by TEX code.--> | Out of 81 formulas, 70 were replaced by TEX code.--> | ||
| − | {{TEX|semi-auto}}{{TEX| | + | {{TEX|semi-auto}}{{TEX|part}} |
In [[Riemannian geometry|Riemannian geometry]] one has a [[Manifold|manifold]] $M$ of dimension $n$ which admits a [[Metric tensor|metric tensor]] $g$ whose signature is arbitrary. Let $\Gamma$ be the unique [[Levi-Civita connection|Levi-Civita connection]] on $M$ arising from $g$ and let $\mathcal{R}$ be the associated [[Curvature tensor|curvature tensor]] with components <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w120/w120120/w1201208.png"/>. Of importance in Riemannian geometry is the idea of a conformal change of metric, that is, the replacement of the metric $g$ by the metric $\phi g$ where $\phi$ is a nowhere-zero real-valued function on $M$. The metrics $g$ and $g ^ { \prime }$ are then said to be conformally related (or $g ^ { \prime }$ is said to be "conformal" to $g$). One now asks for the existence of a tensor on $M$ which is constructed from the original metric on $M$ and which would be unchanged if it were to be replaced with another metric conformally related to it. (It is noted here that the curvature tensor would only be unaffected by such a change, in general, if the function $\phi$ were constant.) The answer was provided mainly by H. Weyl [[#References|[a1]]], but with important contributions from J.A. Schouten [[#References|[a2]]] (see also [[#References|[a3]]]). For $n > 3$, Weyl constructed the tensor $C$ (now called the Weyl tensor) with components given by | In [[Riemannian geometry|Riemannian geometry]] one has a [[Manifold|manifold]] $M$ of dimension $n$ which admits a [[Metric tensor|metric tensor]] $g$ whose signature is arbitrary. Let $\Gamma$ be the unique [[Levi-Civita connection|Levi-Civita connection]] on $M$ arising from $g$ and let $\mathcal{R}$ be the associated [[Curvature tensor|curvature tensor]] with components <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w120/w120120/w1201208.png"/>. Of importance in Riemannian geometry is the idea of a conformal change of metric, that is, the replacement of the metric $g$ by the metric $\phi g$ where $\phi$ is a nowhere-zero real-valued function on $M$. The metrics $g$ and $g ^ { \prime }$ are then said to be conformally related (or $g ^ { \prime }$ is said to be "conformal" to $g$). One now asks for the existence of a tensor on $M$ which is constructed from the original metric on $M$ and which would be unchanged if it were to be replaced with another metric conformally related to it. (It is noted here that the curvature tensor would only be unaffected by such a change, in general, if the function $\phi$ were constant.) The answer was provided mainly by H. Weyl [[#References|[a1]]], but with important contributions from J.A. Schouten [[#References|[a2]]] (see also [[#References|[a3]]]). For $n > 3$, Weyl constructed the tensor $C$ (now called the Weyl tensor) with components given by | ||
Latest revision as of 17:47, 1 July 2020
In Riemannian geometry one has a manifold $M$ of dimension $n$ which admits a metric tensor $g$ whose signature is arbitrary. Let $\Gamma$ be the unique Levi-Civita connection on $M$ arising from $g$ and let $\mathcal{R}$ be the associated curvature tensor with components  . Of importance in Riemannian geometry is the idea of a conformal change of metric, that is, the replacement of the metric $g$ by the metric $\phi g$ where $\phi$ is a nowhere-zero real-valued function on $M$. The metrics $g$ and $g ^ { \prime }$ are then said to be conformally related (or $g ^ { \prime }$ is said to be "conformal" to $g$). One now asks for the existence of a tensor on $M$ which is constructed from the original metric on $M$ and which would be unchanged if it were to be replaced with another metric conformally related to it. (It is noted here that the curvature tensor would only be unaffected by such a change, in general, if the function $\phi$ were constant.) The answer was provided mainly by H. Weyl [a1], but with important contributions from J.A. Schouten [a2] (see also [a3]). For $n > 3$, Weyl constructed the tensor $C$ (now called the Weyl tensor) with components given by
. Of importance in Riemannian geometry is the idea of a conformal change of metric, that is, the replacement of the metric $g$ by the metric $\phi g$ where $\phi$ is a nowhere-zero real-valued function on $M$. The metrics $g$ and $g ^ { \prime }$ are then said to be conformally related (or $g ^ { \prime }$ is said to be "conformal" to $g$). One now asks for the existence of a tensor on $M$ which is constructed from the original metric on $M$ and which would be unchanged if it were to be replaced with another metric conformally related to it. (It is noted here that the curvature tensor would only be unaffected by such a change, in general, if the function $\phi$ were constant.) The answer was provided mainly by H. Weyl [a1], but with important contributions from J.A. Schouten [a2] (see also [a3]). For $n > 3$, Weyl constructed the tensor $C$ (now called the Weyl tensor) with components given by
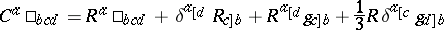 | (a1) |
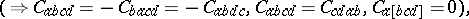 |
where $R _ { ab } \equiv R ^ { c } \square _ { a c b }$ are the Ricci tensor components, 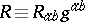 is the Ricci scalar and square brackets denote the usual skew-symmetrization of indices. If this tensor is written out in terms of the metric $g$ and its first- and second-order derivatives, it can then be shown to be unchanged if $g$ is replaced by the metric $g ^ { \prime }$. (It should be noted that this is not true of the tensor with components $C_{abcd}$, which would be scaled by a factor $\phi$ on exchanging $g$ for $g ^ { \prime }$.) If $g$ is a flat metric (so that $\mathcal{R} = 0$), then the Weyl tensor constructed from $g$ (and from $g ^ { \prime }$) is zero on $M$. Conversely, if $g$ gives rise, from (a1), to a zero Weyl tensor on $M$, then for each $p$ in $M$ there are a neighbourhood $U$ of $p$ in $M$, a real-valued function $\psi$ on $U$ and a flat metric $h$ on $U$ such that $g = \psi h$ on $U$ (i.e. $g$ is locally conformal to a flat metric on $M$). When $C = 0$ on $M$, the latter is called conformally flat.
is the Ricci scalar and square brackets denote the usual skew-symmetrization of indices. If this tensor is written out in terms of the metric $g$ and its first- and second-order derivatives, it can then be shown to be unchanged if $g$ is replaced by the metric $g ^ { \prime }$. (It should be noted that this is not true of the tensor with components $C_{abcd}$, which would be scaled by a factor $\phi$ on exchanging $g$ for $g ^ { \prime }$.) If $g$ is a flat metric (so that $\mathcal{R} = 0$), then the Weyl tensor constructed from $g$ (and from $g ^ { \prime }$) is zero on $M$. Conversely, if $g$ gives rise, from (a1), to a zero Weyl tensor on $M$, then for each $p$ in $M$ there are a neighbourhood $U$ of $p$ in $M$, a real-valued function $\psi$ on $U$ and a flat metric $h$ on $U$ such that $g = \psi h$ on $U$ (i.e. $g$ is locally conformal to a flat metric on $M$). When $C = 0$ on $M$, the latter is called conformally flat.
If $n = 3$, it can be shown from (a1) that $C \equiv 0$ on $M$. Since not every metric on such a manifold is locally conformally related to a flat metric, the tensor $C$ is no longer appropriate. The situation was resolved by Schouten [a2] when he found that the tensor given in components by
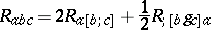 | (a2) |
(using a semi-colon to denote a covariant derivative with respect to the Levi-Civita connection arising from the metric) played exactly the same role in dimension $3$ as did $C$ for $n > 3$. If $n = 2$, every metric on $M$ is locally conformally related to a flat metric [a3].
The tensor $C$ has all the usual algebraic symmetries of the curvature tensor, together with the extra relation 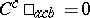 . If the Ricci tensor is zero on $M$, the Weyl tensor and the curvature tensor are equal on $M$. The tensor introduced in (a2) by Schouten possesses the algebraic identities
. If the Ricci tensor is zero on $M$, the Weyl tensor and the curvature tensor are equal on $M$. The tensor introduced in (a2) by Schouten possesses the algebraic identities
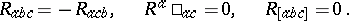 | (a3) |
It is interesting to ask if two metrics on $M$ ($n > 3$) having the same Weyl tensor as in (a1) are necessarily (locally) conformally related. The answer is clearly no if $C = 0$. If $C$ is not zero on $M$, the answer is still no, a counter-example (at least) being available for a space-time manifold (i.e. a $4$-dimensional manifold admitting a metric with Lorentz signature $( + + + - )$).
The Weyl tensor finds many uses in differential geometry and also in Einstein's general relativity theory. In the latter it has important physical interpretations and its algebraic classification is the famous Petrov classification of gravitational fields [a4]
References
| [a1] | H. Weyl, "Reine Infinitesimalgeometrie" Math. Z. , 2 (1918) pp. 384–411 |
| [a2] | J.A. Schouten, "Ueber die konforme Abbildung $n$-dimensionaler Mannigfaltigkeiten mit quadratischer Massbestimmung auf eine Mannigfaltigkeit mit Euklidischer Massbestimmung" Math. Z. , 11 (1921) pp. 58–88 |
| [a3] | L.P. Eisenhart, "Riemannian geometry" , Princeton Univ. Press (1966) |
| [a4] | A.Z. Petrov., "Einstein spaces" , Pergamon (1969) |
Weyl tensor. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weyl_tensor&oldid=50848