Let  be a classical Hamiltonian (cf. also Hamilton operator) defined on
be a classical Hamiltonian (cf. also Hamilton operator) defined on  . The Weyl quantization rule associates to this function the operator
. The Weyl quantization rule associates to this function the operator  defined on functions
defined on functions  as
as
 | (a1) |
For instance,  , with
, with
whereas the classical quantization rule would map the Hamiltonian  to the operator
to the operator  . A nice feature of the Weyl quantization rule, introduced in 1928 by H. Weyl [a12], is the fact that real Hamiltonians get quantized by (formally) self-adjoint operators. Recall that the classical quantization of the Hamiltonian
. A nice feature of the Weyl quantization rule, introduced in 1928 by H. Weyl [a12], is the fact that real Hamiltonians get quantized by (formally) self-adjoint operators. Recall that the classical quantization of the Hamiltonian  is given by the operator
is given by the operator  acting on functions
acting on functions 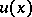 by
by
 | (a2) |
where the Fourier transform 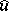 is defined by
is defined by
 | (a3) |
so that  , with
, with 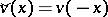 . In fact, introducing the one-parameter group
. In fact, introducing the one-parameter group 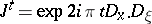 , given by the integral formula
, given by the integral formula
 | (a4) |
one sees that
In particular, one gets  . Moreover, since
. Moreover, since  one obtains
one obtains
yielding formal self-adjointness for real  (cf. also Self-adjoint operator).
(cf. also Self-adjoint operator).
Wigner functions.
Formula (a1) can be written as
 | (a5) |
where the Wigner function  is defined as
is defined as
 | (a6) |
The mapping  is sesquilinear continuous from
is sesquilinear continuous from 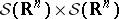 to
to  , so that
, so that 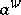 makes sense for
makes sense for  (here,
(here,  and
and  stands for the anti-dual):
stands for the anti-dual):
The Wigner function also satisfies
and the phase symmetries  are unitary and self-adjoint operators on
are unitary and self-adjoint operators on 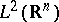 . Also ([a10], [a12]),
. Also ([a10], [a12]),
where 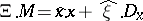 (here
(here 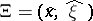 ). These formulas give, in particular,
). These formulas give, in particular,
where 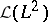 stands for the space of bounded linear mappings from
stands for the space of bounded linear mappings from 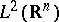 into itself. The operator
into itself. The operator 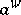 is in the Hilbert–Schmidt class (cf. also Hilbert–Schmidt operator) if and only if
is in the Hilbert–Schmidt class (cf. also Hilbert–Schmidt operator) if and only if  belongs to
belongs to  and
and 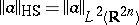 . To get this, it suffices to notice the relationship between the symbol
. To get this, it suffices to notice the relationship between the symbol  of
of 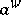 and its distribution kernel
and its distribution kernel  :
:
The Fourier transform of the Wigner function is the so-called ambiguity function
 | (a7) |
For 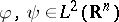 , the Wigner function
, the Wigner function 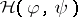 is the Weyl symbol of the operator
is the Weyl symbol of the operator 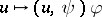 (cf. also Symbol of an operator), where
(cf. also Symbol of an operator), where 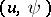 is the
is the  (Hermitian) dot-product, so that from (a5) one finds
(Hermitian) dot-product, so that from (a5) one finds
As is shown below, the symplectic invariance of the Weyl quantization is actually its most important property.
Symplectic invariance.
Consider a finite-dimensional real vector space 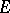 (the configuration space
(the configuration space 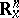 ) and its dual space
) and its dual space 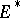 (the momentum space
(the momentum space  ). The phase space is defined as
). The phase space is defined as  ; its running point will be denoted, in general, by a capital letter (
; its running point will be denoted, in general, by a capital letter (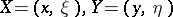 ). The symplectic form (cf. also Symplectic connection) on
). The symplectic form (cf. also Symplectic connection) on 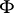 is given by
is given by
 | (a8) |
where  stands for the bracket of duality. The symplectic group is the subgroup of the linear group of
stands for the bracket of duality. The symplectic group is the subgroup of the linear group of  preserving (a8). With
preserving (a8). With
for 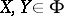 one has
one has
so that the equation of the symplectic group is
One can describe a set of generators for the symplectic group  , identifying
, identifying 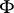 with
with 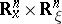 : the mappings
: the mappings
i) 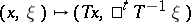 , where
, where 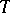 is an automorphism of
is an automorphism of  ;
;
ii) 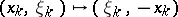 and the other coordinates fixed;
and the other coordinates fixed;
iii) 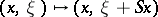 , where
, where 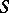 is symmetric from
is symmetric from 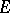 to
to  . One then describes the metaplectic group, introduced by A. Weil [a11]. The metaplectic group
. One then describes the metaplectic group, introduced by A. Weil [a11]. The metaplectic group  is the subgroup of the group of unitary transformations of
is the subgroup of the group of unitary transformations of 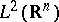 generated by
generated by
j) 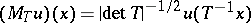 , where
, where 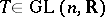 ;
;
jj) partial Fourier transformations;
jjj) multiplication by 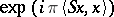 , where
, where  is a symmetric matrix. There exists a two-fold covering (the
is a symmetric matrix. There exists a two-fold covering (the  of both
of both  and
and 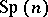 is
is  )
)
such that, if  and
and  ,
,  are in
are in 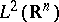 , while
, while 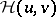 is their Wigner function, then
is their Wigner function, then
This is Segal's formula [a9], which can be rephrased as follows. Let 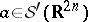 and
and  . There exists an
. There exists an  in the fibre of
in the fibre of  such that
such that
 | (a9) |
In particular, the images by  of the transformations j), jj), jjj) are, respectively, i), ii), iii). Moreover, if
of the transformations j), jj), jjj) are, respectively, i), ii), iii). Moreover, if 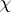 is the phase translation,
is the phase translation, 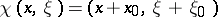 , (a9) is fulfilled with
, (a9) is fulfilled with 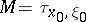 and phase translation given by
and phase translation given by
If 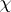 is the symmetry with respect to
is the symmetry with respect to 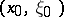 ,
, 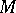 in (a9) is, up to a unit factor, the phase symmetry
in (a9) is, up to a unit factor, the phase symmetry  defined above. This yields the following composition formula:
defined above. This yields the following composition formula: 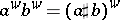 with
with
 | (a10) |
with an integral on 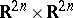 . One can compare this with the classical composition formula,
. One can compare this with the classical composition formula,
(cf. (a2)) with
with an integral on  . It is convenient to give an asymptotic version of these compositions formulas, e.g. in the semi-classical case. Let
. It is convenient to give an asymptotic version of these compositions formulas, e.g. in the semi-classical case. Let 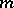 be a real number. A smooth function
be a real number. A smooth function 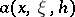 defined on
defined on 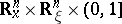 is in the symbol class
is in the symbol class 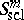 if
if
Then one has for 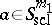 and
and 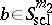 the expansion
the expansion
 | (a11) |
with 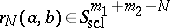 . The beginning of this expansion is thus
. The beginning of this expansion is thus
where 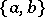 denotes the Poisson brackets and
denotes the Poisson brackets and  . The sums inside (a11) with
. The sums inside (a11) with 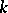 even are symmetric in
even are symmetric in  and skew-symmetric for
and skew-symmetric for 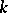 odd. This can be compared to the classical expansion formula
odd. This can be compared to the classical expansion formula
with  . Moreover, for
. Moreover, for  in
in  , the multiple composition formula gives
, the multiple composition formula gives
and if 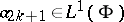 ,
,
Consider the standard sum of homogeneous symbols defined on  , where
, where  is an open subset of
is an open subset of 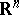 ,
,
with  smooth on
smooth on 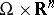 and homogeneous in the following sense:
and homogeneous in the following sense:
and  , i.e. for all compact subsets
, i.e. for all compact subsets  of
of  ,
,
This class of pseudo-differential operators (cf. also Pseudo-differential operator) is invariant under diffeomorphisms, and using the Weyl quantization one gets that the principal symbol  is invariantly defined on the cotangent bundle
is invariantly defined on the cotangent bundle 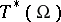 whereas the subprincipal symbol
whereas the subprincipal symbol  is invariantly defined on the double characteristic set
is invariantly defined on the double characteristic set
of the principal symbol. If one writes
one gets 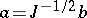 and
and  . Moreover,
. Moreover,
Thus, if one defines the subprincipal symbol as the above analytic expression 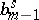 where
where 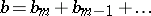 is the classical symbol of
is the classical symbol of 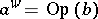 , one finds that this invariant
, one finds that this invariant  is simply the second term
is simply the second term 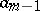 in the expansion of the Weyl symbol
in the expansion of the Weyl symbol  . In the same vein, it is also useful to note that when considering pseudo-differential operators acting on half-densities one gets a refined principal symbol
. In the same vein, it is also useful to note that when considering pseudo-differential operators acting on half-densities one gets a refined principal symbol 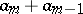 invariant by diffeomorphism.
invariant by diffeomorphism.
Weyl–Hörmander calculus and admissible metrics.
The developments of the analysis of partial differential operators in the 1970s required refined localizations in the phase space. E.g., the Beals–Fefferman local solvability theorem [a2] yields the geometric condition (P) as an if-and-only-if solvability condition for differential operators of principal type (with possibly complex symbols). These authors removed the analyticity assumption used by L. Nirenberg and F. Treves, and a key point in their method is a Calderón–Zygmund decomposition of the symbol, that is, a micro-localization procedure depending on a particular function, yielding a pseudo-differential calculus tailored to the symbol under investigation. Another example is provided by the Fefferman–Phong inequality [a6], establishing that second-order operators with non-negative symbols are bounded from below on 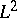 ; a Calderón–Zygmund decomposition is needed in the proof, as well as an induction on the number of variables. These micro-localizations go much beyond the standard homogeneous calculus and also beyond the classes
; a Calderón–Zygmund decomposition is needed in the proof, as well as an induction on the number of variables. These micro-localizations go much beyond the standard homogeneous calculus and also beyond the classes 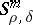 , previously called exotic. In 1979, L.V. Hörmander published [a7], providing simple and general rules for a pseudo-differential calculus to be admissible. Consider a positive-definite quadratic form
, previously called exotic. In 1979, L.V. Hörmander published [a7], providing simple and general rules for a pseudo-differential calculus to be admissible. Consider a positive-definite quadratic form 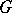 defined on
defined on 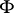 . The dual quadratic form
. The dual quadratic form 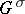 with respect to the symplectic structure is
with respect to the symplectic structure is
 | (a12) |
Define an admissible metric on the phase space as a mapping from 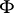 to the set of positive-definite quadratic forms on
to the set of positive-definite quadratic forms on  ,
,  , such that the following three properties are fulfilled:
, such that the following three properties are fulfilled:
(uncertainty principle) For all 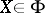 ,
,
 | (a13) |
there exist some positive constants 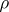 ,
,  , such that, for all
, such that, for all  ,
,
 | (a14) |
there exist some positive constants 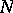 ,
, 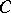 , such that, for all
, such that, for all  ,
,
 | (a15) |
Property (a13) is clearly related to the uncertainty principle, since for each  one can diagonalize the quadratic form
one can diagonalize the quadratic form 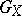 in a symplectic basis so that
in a symplectic basis so that
where  is a set of symplectic coordinates. One then gets
is a set of symplectic coordinates. One then gets
Condition (a13) thus means that  , which can be rephrased in the familiarly vague version as
, which can be rephrased in the familiarly vague version as
in the 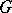 -balls. This condition is relevant to any micro-localization procedure. When
-balls. This condition is relevant to any micro-localization procedure. When  , one says that the quadratic form is symplectic. Property (a14) is called slowness of the metric and is usually easy to verify. Property (a15) is the temperance of the metric and is more of a technical character, although very important in handling non-local terms in the composition formula. In particular, this property is useful to verify the assumptions of Cotlar's lemma. Moreover, one defines a weight
, one says that the quadratic form is symplectic. Property (a14) is called slowness of the metric and is usually easy to verify. Property (a15) is the temperance of the metric and is more of a technical character, although very important in handling non-local terms in the composition formula. In particular, this property is useful to verify the assumptions of Cotlar's lemma. Moreover, one defines a weight 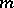 as a positive function on
as a positive function on  such that there exist positive constants
such that there exist positive constants 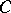 ,
, 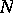 so that for all
so that for all 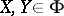 ,
,
 | (a16) |
and
 | (a17) |
Eventually, one defines the class of symbols 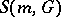 as the
as the 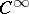 -functions
-functions  on the phase space such that
on the phase space such that
 | (a18) |
It is, for instance, easily checked that
with  and that this metric is an admissible metric when
and that this metric is an admissible metric when 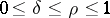 ,
, 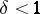 . The metric defining
. The metric defining 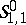 satisfies (a13)–(a14) but fails to satisfy (a15). Indeed, there are counterexamples showing that for the classical and the Weyl quantization [a4] there are symbols in
satisfies (a13)–(a14) but fails to satisfy (a15). Indeed, there are counterexamples showing that for the classical and the Weyl quantization [a4] there are symbols in 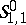 whose quantization is not
whose quantization is not  -bounded. In fact, one of the building block for the calculus of pseudo-differential operators is the
-bounded. In fact, one of the building block for the calculus of pseudo-differential operators is the  -boundedness of the Weyl quantization of symbols in
-boundedness of the Weyl quantization of symbols in 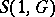 , where
, where 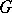 is an admissible metric. One defines the Planck function of the calculus as
is an admissible metric. One defines the Planck function of the calculus as
 | (a19) |
and notes that from (a13),  . One obtains the composition formula (a11) with
. One obtains the composition formula (a11) with  ,
,  and
and  . In particular, one obtains, with obvious notations,
. In particular, one obtains, with obvious notations,
The Fefferman–Phong inequality has also a simple expression in this framework: Let  be a non-negative symbol in
be a non-negative symbol in 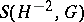 , then the operator
, then the operator 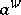 is semi-bounded from below in
is semi-bounded from below in 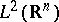 . The proof uses a Calderón–Zygmund decomposition and in fact one shows that
. The proof uses a Calderón–Zygmund decomposition and in fact one shows that 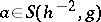 , where
, where  is the Planck function related to the admissible metric
is the Planck function related to the admissible metric 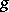 defined by
defined by
On the other hand, if 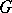 is an admissible metric and
is an admissible metric and 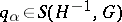 uniformly with respect to a parameter
uniformly with respect to a parameter  , the following metric also satisfies (a13)–(a15):
, the following metric also satisfies (a13)–(a15): 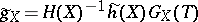 , with
, with
One gets in this case that  uniformly. A key point in the Beals–Fefferman proof of local solvability under condition (P) can be reformulated through the construction of the previous metric. Sobolev spaces related to this type of calculus were studied in [a1] (cf. also Sobolev space). For an admissible metric
uniformly. A key point in the Beals–Fefferman proof of local solvability under condition (P) can be reformulated through the construction of the previous metric. Sobolev spaces related to this type of calculus were studied in [a1] (cf. also Sobolev space). For an admissible metric  and a weight
and a weight 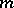 , the space
, the space  is defined as
is defined as
It can be proven that a Hilbertian structure can be set on 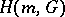 , that
, that 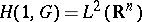 and that for
and that for 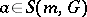 and
and 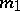 another weight, the mapping
another weight, the mapping
is continuous.
Further developments of the Weyl calculus were explored in [a3], with higher-order micro-localizations. Several metrics
are given on the phase space. All these metrics satisfy (a13)–(a14), but, except for 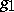 , fail to satisfy globally the temperance condition (a15). Instead, the metric
, fail to satisfy globally the temperance condition (a15). Instead, the metric 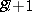 is assumed to be (uniformly) temperate on the
is assumed to be (uniformly) temperate on the  -balls. It is then possible to produce a satisfactory quantization formula for symbols belonging to a class
-balls. It is then possible to produce a satisfactory quantization formula for symbols belonging to a class  . A typical example is given in [a5], with applications to propagation of singularities for non-linear hyperbolic equations:
. A typical example is given in [a5], with applications to propagation of singularities for non-linear hyperbolic equations:
where 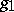 is defined on
is defined on  , and
, and  on
on
It is then possible to quantize functions 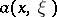 homogeneous of degree
homogeneous of degree  in the variable
in the variable  , and
, and  in the variable
in the variable  , so as to get composition formulas, Sobolev spaces, and the standard pseudo-differential apparatus allowing a commutator argument to work for propagation results.
, so as to get composition formulas, Sobolev spaces, and the standard pseudo-differential apparatus allowing a commutator argument to work for propagation results.
References
| [a1] | J.-M. Bony, J.-Y. Chemin, "Espaces fonctionnels associés au calcul de Weyl–Hörmander" Bull. Soc. Math. France , 122 (1994) pp. 77–118 |
| [a2] | R. Beals, C. Fefferman, "On local solvability of linear partial differential equations" Ann. of Math. , 97 (1973) pp. 482–498 |
| [a3] | J.-M. Bony, N. Lerner, "Quantification asymtotique et microlocalisations d'ordre supérieur" Ann. Sci. Ecole Norm. Sup. , 22 (1989) pp. 377–483 |
| [a4] | A. Boulkhemair, "Remarque sur la quantification de Weyl pour la classe de symboles 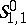 " C.R. Acad. Sci. Paris , 321 : 8 (1995) pp. 1017–1022 " C.R. Acad. Sci. Paris , 321 : 8 (1995) pp. 1017–1022 |
| [a5] | J.-M. Bony, "Second microlocalization and propagation of singularities for semi-linear hyperbolic equations" K. Mizohata (ed.) , Hyperbolic Equations and Related Topics , Kinokuniya (1986) pp. 11–49 |
| [a6] | C. Fefferman, D.H. Phong, "On positivity of pseudo-differential operators" Proc. Nat. Acad. Sci. USA , 75 (1978) pp. 4673–4674 |
| [a7] | L. Hörmander, "The Weyl calculus of pseudo-differential operators" Commun. Pure Appl. Math. , 32 (1979) pp. 359–443 |
| [a8] | L. Hörmander, "The analysis of linear partial differential operators III-IV" , Springer (1985) |
| [a9] | I. Segal, "Transforms for operators and asymptotic automorphisms over a locally compact abelian group" Math. Scand. , 13 (1963) pp. 31–43 |
| [a10] | A. Unterberger, "Oscillateur harmonique et opérateurs pseudo-différentiels" Ann. Inst. Fourier , 29 : 3 (1979) pp. 201–221 |
| [a11] | A. Weil, "Sur certains groupes d'opérateurs unitaires" Acta Math. , 111 (1964) pp. 143–211 |
| [a12] | H. Weyl, "Gruppentheorie und Quantenmechanik" , S. Hirzel (1928) |
 be a classical Hamiltonian (cf. also Hamilton operator) defined on
be a classical Hamiltonian (cf. also Hamilton operator) defined on  . The Weyl quantization rule associates to this function the operator
. The Weyl quantization rule associates to this function the operator  defined on functions
defined on functions  as
as

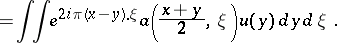
 , with
, with
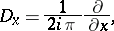
 to the operator
to the operator  . A nice feature of the Weyl quantization rule, introduced in 1928 by H. Weyl [a12], is the fact that real Hamiltonians get quantized by (formally) self-adjoint operators. Recall that the classical quantization of the Hamiltonian
. A nice feature of the Weyl quantization rule, introduced in 1928 by H. Weyl [a12], is the fact that real Hamiltonians get quantized by (formally) self-adjoint operators. Recall that the classical quantization of the Hamiltonian  is given by the operator
is given by the operator  acting on functions
acting on functions 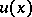 by
by

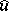 is defined by
is defined by

 , with
, with 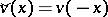 . In fact, introducing the one-parameter group
. In fact, introducing the one-parameter group 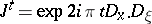 , given by the integral formula
, given by the integral formula

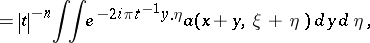
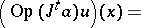
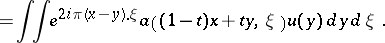
 . Moreover, since
. Moreover, since  one obtains
one obtains
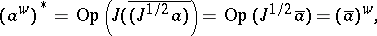
 (cf. also Self-adjoint operator).
(cf. also Self-adjoint operator).

 is defined as
is defined as

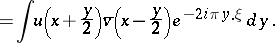
 is sesquilinear continuous from
is sesquilinear continuous from 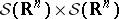 to
to  , so that
, so that 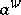 makes sense for
makes sense for  (here,
(here,  and
and  stands for the anti-dual):
stands for the anti-dual):
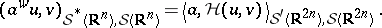
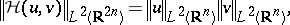

 are unitary and self-adjoint operators on
are unitary and self-adjoint operators on 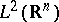 . Also ([a10], [a12]),
. Also ([a10], [a12]),
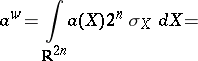
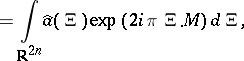
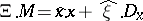 (here
(here 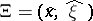 ). These formulas give, in particular,
). These formulas give, in particular,
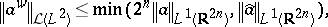
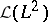 stands for the space of bounded linear mappings from
stands for the space of bounded linear mappings from 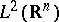 into itself. The operator
into itself. The operator 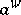 is in the Hilbert–Schmidt class (cf. also Hilbert–Schmidt operator) if and only if
is in the Hilbert–Schmidt class (cf. also Hilbert–Schmidt operator) if and only if  belongs to
belongs to  and
and 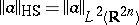 . To get this, it suffices to notice the relationship between the symbol
. To get this, it suffices to notice the relationship between the symbol  of
of 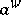 and its distribution kernel
and its distribution kernel  :
:
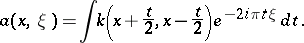

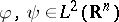 , the Wigner function
, the Wigner function 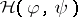 is the Weyl symbol of the operator
is the Weyl symbol of the operator 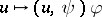 (cf. also Symbol of an operator), where
(cf. also Symbol of an operator), where 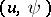 is the
is the  (Hermitian) dot-product, so that from (a5) one finds
(Hermitian) dot-product, so that from (a5) one finds
 (the configuration space
(the configuration space  ) and its dual space
) and its dual space 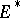 (the momentum space
(the momentum space  ). The phase space is defined as
). The phase space is defined as  ; its running point will be denoted, in general, by a capital letter (
; its running point will be denoted, in general, by a capital letter (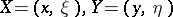 ). The symplectic form (cf. also Symplectic connection) on
). The symplectic form (cf. also Symplectic connection) on 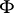 is given by
is given by

 stands for the bracket of duality. The symplectic group is the subgroup of the linear group of
stands for the bracket of duality. The symplectic group is the subgroup of the linear group of  preserving (a8). With
preserving (a8). With

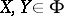 one has
one has
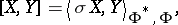
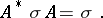
 , identifying
, identifying 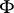 with
with 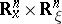 : the mappings
: the mappings
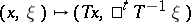 , where
, where 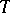 is an automorphism of
is an automorphism of  ;
;
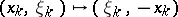 and the other coordinates fixed;
and the other coordinates fixed;
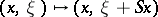 , where
, where 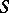 is symmetric from
is symmetric from 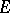 to
to  . One then describes the metaplectic group, introduced by A. Weil [a11]. The metaplectic group
. One then describes the metaplectic group, introduced by A. Weil [a11]. The metaplectic group  is the subgroup of the group of unitary transformations of
is the subgroup of the group of unitary transformations of 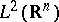 generated by
generated by
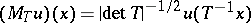 , where
, where 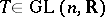 ;
;
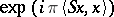 , where
, where  is a symmetric matrix. There exists a two-fold covering (the
is a symmetric matrix. There exists a two-fold covering (the  of both
of both  and
and 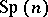 is
is  )
)
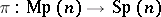
 and
and  ,
,  are in
are in 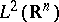 , while
, while 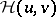 is their Wigner function, then
is their Wigner function, then
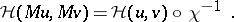
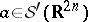 and
and  . There exists an
. There exists an  in the fibre of
in the fibre of  such that
such that

 of the transformations j), jj), jjj) are, respectively, i), ii), iii). Moreover, if
of the transformations j), jj), jjj) are, respectively, i), ii), iii). Moreover, if 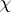 is the phase translation,
is the phase translation, 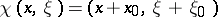 , (a9) is fulfilled with
, (a9) is fulfilled with 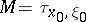 and phase translation given by
and phase translation given by
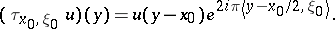
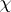 is the symmetry with respect to
is the symmetry with respect to 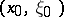 ,
, 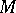 in (a9) is, up to a unit factor, the phase symmetry
in (a9) is, up to a unit factor, the phase symmetry  defined above. This yields the following composition formula:
defined above. This yields the following composition formula: 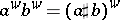 with
with

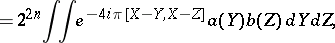
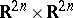 . One can compare this with the classical composition formula,
. One can compare this with the classical composition formula,
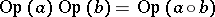
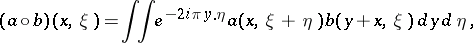
 . It is convenient to give an asymptotic version of these compositions formulas, e.g. in the semi-classical case. Let
. It is convenient to give an asymptotic version of these compositions formulas, e.g. in the semi-classical case. Let 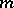 be a real number. A smooth function
be a real number. A smooth function 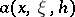 defined on
defined on 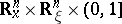 is in the symbol class
is in the symbol class 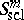 if
if
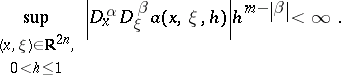
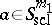 and
and 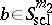 the expansion
the expansion

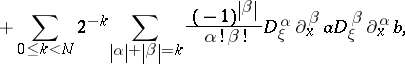
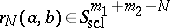 . The beginning of this expansion is thus
. The beginning of this expansion is thus
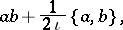
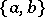 denotes the Poisson brackets and
denotes the Poisson brackets and  . The sums inside (a11) with
. The sums inside (a11) with 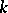 even are symmetric in
even are symmetric in  and skew-symmetric for
and skew-symmetric for 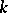 odd. This can be compared to the classical expansion formula
odd. This can be compared to the classical expansion formula

 . Moreover, for
. Moreover, for  in
in  , the multiple composition formula gives
, the multiple composition formula gives
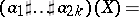
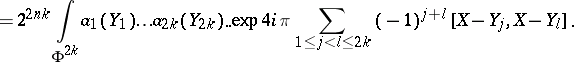
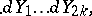
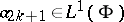 ,
,
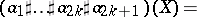
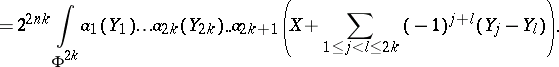
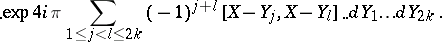
 , where
, where  is an open subset of
is an open subset of 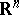 ,
,
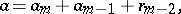
 smooth on
smooth on 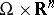 and homogeneous in the following sense:
and homogeneous in the following sense:
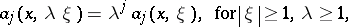
 , i.e. for all compact subsets
, i.e. for all compact subsets  of
of  ,
,
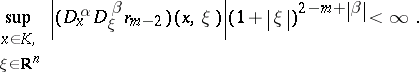
 is invariantly defined on the cotangent bundle
is invariantly defined on the cotangent bundle 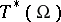 whereas the subprincipal symbol
whereas the subprincipal symbol  is invariantly defined on the double characteristic set
is invariantly defined on the double characteristic set

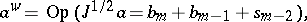
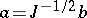 and
and  . Moreover,
. Moreover,
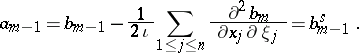
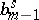 where
where 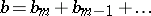 is the classical symbol of
is the classical symbol of 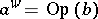 , one finds that this invariant
, one finds that this invariant  is simply the second term
is simply the second term 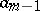 in the expansion of the Weyl symbol
in the expansion of the Weyl symbol  . In the same vein, it is also useful to note that when considering pseudo-differential operators acting on half-densities one gets a refined principal symbol
. In the same vein, it is also useful to note that when considering pseudo-differential operators acting on half-densities one gets a refined principal symbol 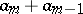 invariant by diffeomorphism.
invariant by diffeomorphism.
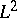 ; a Calderón–Zygmund decomposition is needed in the proof, as well as an induction on the number of variables. These micro-localizations go much beyond the standard homogeneous calculus and also beyond the classes
; a Calderón–Zygmund decomposition is needed in the proof, as well as an induction on the number of variables. These micro-localizations go much beyond the standard homogeneous calculus and also beyond the classes 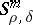 , previously called exotic. In 1979, L.V. Hörmander published [a7], providing simple and general rules for a pseudo-differential calculus to be admissible. Consider a positive-definite quadratic form
, previously called exotic. In 1979, L.V. Hörmander published [a7], providing simple and general rules for a pseudo-differential calculus to be admissible. Consider a positive-definite quadratic form 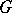 defined on
defined on 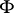 . The dual quadratic form
. The dual quadratic form 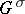 with respect to the symplectic structure is
with respect to the symplectic structure is

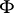 to the set of positive-definite quadratic forms on
to the set of positive-definite quadratic forms on  ,
,  , such that the following three properties are fulfilled:
, such that the following three properties are fulfilled:
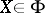 ,
,

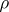 ,
,  , such that, for all
, such that, for all  ,
,

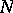 ,
, 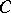 , such that, for all
, such that, for all  ,
,

 one can diagonalize the quadratic form
one can diagonalize the quadratic form 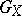 in a symplectic basis so that
in a symplectic basis so that
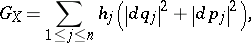
 is a set of symplectic coordinates. One then gets
is a set of symplectic coordinates. One then gets

 , which can be rephrased in the familiarly vague version as
, which can be rephrased in the familiarly vague version as
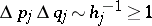
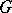 -balls. This condition is relevant to any micro-localization procedure. When
-balls. This condition is relevant to any micro-localization procedure. When  , one says that the quadratic form is symplectic. Property (a14) is called slowness of the metric and is usually easy to verify. Property (a15) is the temperance of the metric and is more of a technical character, although very important in handling non-local terms in the composition formula. In particular, this property is useful to verify the assumptions of Cotlar's lemma. Moreover, one defines a weight
, one says that the quadratic form is symplectic. Property (a14) is called slowness of the metric and is usually easy to verify. Property (a15) is the temperance of the metric and is more of a technical character, although very important in handling non-local terms in the composition formula. In particular, this property is useful to verify the assumptions of Cotlar's lemma. Moreover, one defines a weight 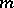 as a positive function on
as a positive function on  such that there exist positive constants
such that there exist positive constants 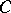 ,
, 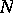 so that for all
so that for all 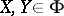 ,
,


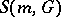 as the
as the 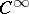 -functions
-functions  on the phase space such that
on the phase space such that

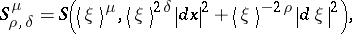
 and that this metric is an admissible metric when
and that this metric is an admissible metric when 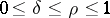 ,
, 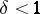 . The metric defining
. The metric defining 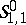 satisfies (a13)–(a14) but fails to satisfy (a15). Indeed, there are counterexamples showing that for the classical and the Weyl quantization [a4] there are symbols in
satisfies (a13)–(a14) but fails to satisfy (a15). Indeed, there are counterexamples showing that for the classical and the Weyl quantization [a4] there are symbols in 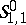 whose quantization is not
whose quantization is not  -bounded. In fact, one of the building block for the calculus of pseudo-differential operators is the
-bounded. In fact, one of the building block for the calculus of pseudo-differential operators is the  -boundedness of the Weyl quantization of symbols in
-boundedness of the Weyl quantization of symbols in 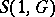 , where
, where 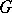 is an admissible metric. One defines the Planck function of the calculus as
is an admissible metric. One defines the Planck function of the calculus as

 . One obtains the composition formula (a11) with
. One obtains the composition formula (a11) with  ,
,  and
and  . In particular, one obtains, with obvious notations,
. In particular, one obtains, with obvious notations,
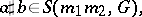
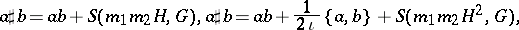
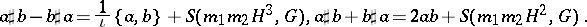
 be a non-negative symbol in
be a non-negative symbol in 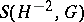 , then the operator
, then the operator 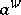 is semi-bounded from below in
is semi-bounded from below in 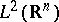 . The proof uses a Calderón–Zygmund decomposition and in fact one shows that
. The proof uses a Calderón–Zygmund decomposition and in fact one shows that 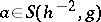 , where
, where  is the Planck function related to the admissible metric
is the Planck function related to the admissible metric 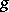 defined by
defined by

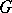 is an admissible metric and
is an admissible metric and 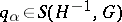 uniformly with respect to a parameter
uniformly with respect to a parameter  , the following metric also satisfies (a13)–(a15):
, the following metric also satisfies (a13)–(a15): 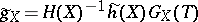 , with
, with
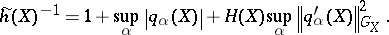
 uniformly. A key point in the Beals–Fefferman proof of local solvability under condition (P) can be reformulated through the construction of the previous metric. Sobolev spaces related to this type of calculus were studied in [a1] (cf. also Sobolev space). For an admissible metric
uniformly. A key point in the Beals–Fefferman proof of local solvability under condition (P) can be reformulated through the construction of the previous metric. Sobolev spaces related to this type of calculus were studied in [a1] (cf. also Sobolev space). For an admissible metric  and a weight
and a weight 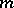 , the space
, the space  is defined as
is defined as
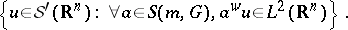
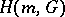 , that
, that 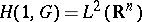 and that for
and that for 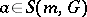 and
and 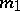 another weight, the mapping
another weight, the mapping
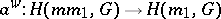
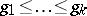
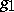 , fail to satisfy globally the temperance condition (a15). Instead, the metric
, fail to satisfy globally the temperance condition (a15). Instead, the metric 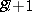 is assumed to be (uniformly) temperate on the
is assumed to be (uniformly) temperate on the  -balls. It is then possible to produce a satisfactory quantization formula for symbols belonging to a class
-balls. It is then possible to produce a satisfactory quantization formula for symbols belonging to a class  . A typical example is given in [a5], with applications to propagation of singularities for non-linear hyperbolic equations:
. A typical example is given in [a5], with applications to propagation of singularities for non-linear hyperbolic equations:
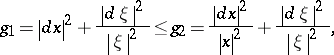
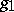 is defined on
is defined on  , and
, and  on
on
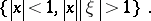
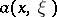 homogeneous of degree
homogeneous of degree  in the variable
in the variable  , and
, and  in the variable
in the variable  , so as to get composition formulas, Sobolev spaces, and the standard pseudo-differential apparatus allowing a commutator argument to work for propagation results.
, so as to get composition formulas, Sobolev spaces, and the standard pseudo-differential apparatus allowing a commutator argument to work for propagation results.
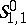 " C.R. Acad. Sci. Paris , 321 : 8 (1995) pp. 1017–1022
" C.R. Acad. Sci. Paris , 321 : 8 (1995) pp. 1017–1022