Weyl criterion
From Encyclopedia of Mathematics
A fundamental criterion used to solve the problem of the uniform distribution of an infinite sequence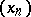 
of arbitrary real numbers 
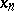modulo 
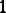, i.e. to establish the existence of the limit
 |
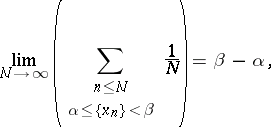where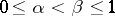 
and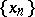 
is the fractional part of 
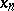(cf. Fractional part of a number). According to Weyl's criterion, the sequence 
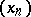is uniformly distributed modulo 
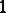if and only if
 |
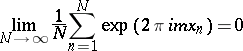for all integers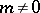 
. Demonstrated in 1916 by H. Weyl. See Weyl method.
References
| [1] | J.W.S. Cassels, "An introduction to diophantine approximation" , Cambridge Univ. Press (1957) |
How to Cite This Entry:
Weyl criterion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weyl_criterion&oldid=11271
Weyl criterion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weyl_criterion&oldid=11271
This article was adapted from an original article by B.M. Bredikhin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article