Weyl calculus
Weyl–Hörmander calculus
In Hamiltonian mechanics over a phase space 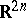 , the Poisson bracket
, the Poisson bracket 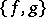 of two smooth observables
of two smooth observables 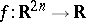 and
and 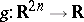 (cf. also Poisson brackets) is the new observable defined by
(cf. also Poisson brackets) is the new observable defined by
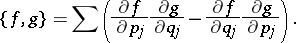 |
For a state 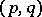 of the phase space
of the phase space 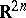 , the momentum vector is given by
, the momentum vector is given by 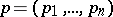 , while
, while 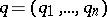 is the position vector. The Poisson brackets of the coordinate functions
is the position vector. The Poisson brackets of the coordinate functions 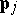 ,
,  are given by
are given by
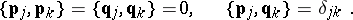 |
By comparison, in quantum mechanics over 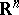 , the position operators
, the position operators 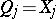 of multiplication by
of multiplication by 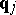 correspond to the classical momentum observables
correspond to the classical momentum observables 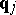 and the momentum operators
and the momentum operators 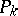 corresponding to the coordinate observables
corresponding to the coordinate observables 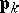 are given by
are given by
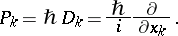 |
The canonical commutation relations
 |
hold for the commutator 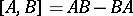 (cf. also Commutation and anti-commutation relationships, representation of).
(cf. also Commutation and anti-commutation relationships, representation of).
In both classical and quantum mechanics, the position, momentum and constant observables span the Heisenberg Lie algebra  over
over 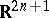 . The Heisenberg group
. The Heisenberg group 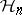 corresponding to the Lie algebra
corresponding to the Lie algebra 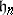 is given on
is given on 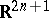 by the group law
by the group law
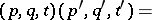 |
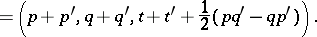 |
Here, one writes 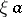 for the dot product
for the dot product 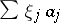 of
of 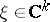 with the
with the 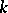 -tuple
-tuple 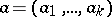 of numbers or operators. Set
of numbers or operators. Set  and
and 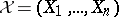 .
.
The mapping 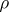 from
from 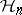 to the group of unitary operators on
to the group of unitary operators on 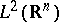 formally defined by
formally defined by 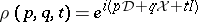 is a unitary representation of the Heisenberg group
is a unitary representation of the Heisenberg group 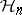 . The operator
. The operator 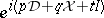 maps
maps 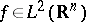 to the function
to the function 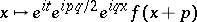 .
.
If 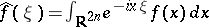 denotes the Fourier transform of a function
denotes the Fourier transform of a function 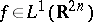 , the Fourier inversion formula
, the Fourier inversion formula
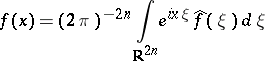 |
retrieves  from
from 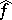 in the case that
in the case that 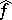 is also integrable.
is also integrable.
Now suppose that 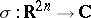 is a function whose Fourier transform
is a function whose Fourier transform 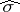 belongs to
belongs to  . Then the bounded linear operator
. Then the bounded linear operator 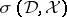 is defined by
is defined by
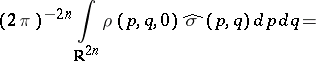 |
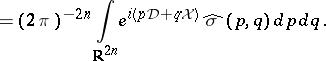 |
The Weyl functional calculus 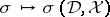 was proposed by H. Weyl [a27], Section IV.14, as a means of associating a quantum observable
was proposed by H. Weyl [a27], Section IV.14, as a means of associating a quantum observable 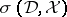 with a classical observable
with a classical observable 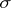 . Weyl's ideas were later developed by H.J. Groenewold [a11], J.E. Moyal [a18] and J.C.T. Pool [a22].
. Weyl's ideas were later developed by H.J. Groenewold [a11], J.E. Moyal [a18] and J.C.T. Pool [a22].
The mapping  extends uniquely to a bijection from the Schwartz space
extends uniquely to a bijection from the Schwartz space 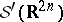 of tempered distributions (cf. also Generalized functions, space of) to the space of continuous linear mappings from
of tempered distributions (cf. also Generalized functions, space of) to the space of continuous linear mappings from 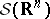 to
to 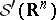 . Moreover, the application
. Moreover, the application 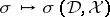 defines a unitary mapping (cf. also Unitary operator) from
defines a unitary mapping (cf. also Unitary operator) from 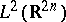 onto the space of Hilbert–Schmidt operators on
onto the space of Hilbert–Schmidt operators on 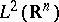 (cf. also Hilbert–Schmidt operator) and from
(cf. also Hilbert–Schmidt operator) and from 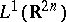 into the space of compact operators on
into the space of compact operators on 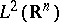 . For
. For 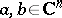 , the function
, the function  is mapped by the Weyl calculus to the operator
is mapped by the Weyl calculus to the operator 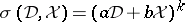 . The monomial terms in any polynomial
. The monomial terms in any polynomial 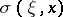 are replaced by symmetric operator products in the expression
are replaced by symmetric operator products in the expression 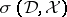 . Harmonic analysis in phase space is a succinct description of this circle of ideas, which is exposed in [a9].
. Harmonic analysis in phase space is a succinct description of this circle of ideas, which is exposed in [a9].
Under the Weyl calculus, the Poisson bracket is mapped to a constant times the commutator only for polynomials 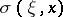 of degree less than or equal to two. Results of Groenewold and L. van Hove [a9], pp. 197–199, show that a quantization over a space of observables defined on a phase space
of degree less than or equal to two. Results of Groenewold and L. van Hove [a9], pp. 197–199, show that a quantization over a space of observables defined on a phase space 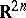 and reasonably larger than the Heisenberg algebra
and reasonably larger than the Heisenberg algebra 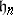 is not possible. A general discussion of obstructions to quantization may be found in [a12].
is not possible. A general discussion of obstructions to quantization may be found in [a12].
In the theory of pseudo-differential operators, initiated by J.J. Kohn and L. Nirenberg [a16], one associates the symbol  with the operator
with the operator  given by
given by
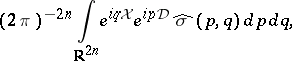 |
so that if 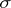 is a polynomial, differentiation always acts first (cf. also Pseudo-differential operator; Symbol of an operator). For singular integral operators (cf. also Singular integral), the product of symbols corresponds to the composition operators modulo regular integral operators. The symbolic calculus for pseudo-differential operators is studied in [a25], [a24], [a14]. The Weyl calculus has been developed as a theory of pseudo-differential operators by L.V. Hörmander [a13], [a14].
is a polynomial, differentiation always acts first (cf. also Pseudo-differential operator; Symbol of an operator). For singular integral operators (cf. also Singular integral), the product of symbols corresponds to the composition operators modulo regular integral operators. The symbolic calculus for pseudo-differential operators is studied in [a25], [a24], [a14]. The Weyl calculus has been developed as a theory of pseudo-differential operators by L.V. Hörmander [a13], [a14].
The Weyl functional calculus can also be formulated in an abstract setting. Suppose that  is a
is a 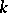 -tuple of operators acting in a Banach space
-tuple of operators acting in a Banach space  , with the property that for each
, with the property that for each 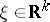 , the operator
, the operator 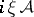 is the generator of a
is the generator of a 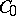 -group of operators such that for some
-group of operators such that for some 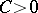 and
and 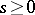 , the bound
, the bound 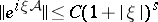 holds for every
holds for every 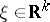 . Then the bounded operator
. Then the bounded operator
 |
is defined for every 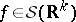 .
.
The operators  do not necessarily commute with one another. Examples are
do not necessarily commute with one another. Examples are 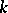 -tuples of bounded self-adjoint operators (cf. also Self-adjoint operator) or, with
-tuples of bounded self-adjoint operators (cf. also Self-adjoint operator) or, with  , the system of unbounded position operators
, the system of unbounded position operators 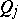 and momentum operators
and momentum operators 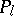 considered above (more accurately, one should use the closure
considered above (more accurately, one should use the closure 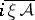 of
of 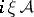 here).
here).
By the Paley–Wiener–Schwartz theorem, the Weyl functional calculus 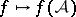 is an operator-valued distribution with compact support if and only if there exists numbers
is an operator-valued distribution with compact support if and only if there exists numbers 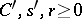 such that
such that
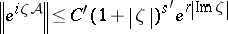 |
for all  . For a
. For a 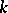 -tuple
-tuple 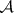 of bounded self-adjoint operators, M. Taylor [a23] has shown that the choice
of bounded self-adjoint operators, M. Taylor [a23] has shown that the choice 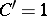 ,
,  and
and 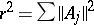 is possible.
is possible.
The Weyl calculus in this setting has been developed by R.F.V. Anderson [a1], [a2], [a3], E. Nelson [a20], and E. Albrecht [a6]. The last two authors provide the connection with the heuristic time-ordered operational calculus of R.P. Feynman [a10] developed in his study of quantum electrodynamics.
A combination of the Weyl and ordered functional calculi is studied in [a17] and [a19].
If the operators 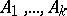 do not commute with each other, then the mapping
do not commute with each other, then the mapping 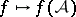 need not be an algebra homomorphism and there may be no spectral mapping property, so the commonly used expression "functional calculus" is somewhat optimistic.
need not be an algebra homomorphism and there may be no spectral mapping property, so the commonly used expression "functional calculus" is somewhat optimistic.
For the case of bounded operators, the Weyl functional calculus 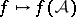 for analytic functions
for analytic functions 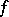 of
of 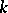 real variables can also be constructed via a Riesz–Dunford calculus by replacing the techniques of complex analysis in one variable with Clifford analysis in
real variables can also be constructed via a Riesz–Dunford calculus by replacing the techniques of complex analysis in one variable with Clifford analysis in 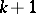 real variables [a15].
real variables [a15].
Given a 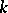 -tuple
-tuple 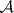 of matrices for which the matrix
of matrices for which the matrix 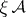 has real eigenvalues for each
has real eigenvalues for each 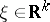 , the distribution
, the distribution 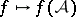 is actually the matrix-valued fundamental solution
is actually the matrix-valued fundamental solution  of the symmetric hyperbolic system
of the symmetric hyperbolic system
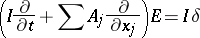 |
at time 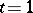 . The study of the support of the Weyl calculus for matrices is intimately related to the theory of lacunas of hyperbolic differential operators and techniques of algebraic geometry [a21], [a7], [a8], [a4], [a5], [a26].
. The study of the support of the Weyl calculus for matrices is intimately related to the theory of lacunas of hyperbolic differential operators and techniques of algebraic geometry [a21], [a7], [a8], [a4], [a5], [a26].
References
| [a1] | R.F.V. Anderson, "The Weyl functional calculus" J. Funct. Anal. , 4 (1969) pp. 240–267 |
| [a2] | R.F.V. Anderson, "On the Weyl functional calculus" J. Funct. Anal. , 6 (1970) pp. 110–115 |
| [a3] | R.F.V. Anderson, "The multiplicative Weyl functional calculus" J. Funct. Anal. , 9 (1972) pp. 423–440 |
| [a4] | M. Atiyah, R. Bott, L. Gårding, "Lacunas for hyperbolic differential operators with constant coefficients I" Acta Math. , 124 (1970) pp. 109–189 |
| [a5] | M. Atiyah, R. Bott, L. Gårding, "Lacunas for hyperbolic differential operators with constant coefficients II" Acta Math. , 131 (1973) pp. 145–206 |
| [a6] | E. Albrecht, "Several variable spectral theory in the non-commutative case" , Spectral Theory , Banach Centre Publ. , 8 , PWN (1982) pp. 9–30 |
| [a7] | J. Bazer, D.H.Y. Yen, "The Riemann matrix of 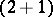 -dimensional symmetric hyperbolic systems" Commun. Pure Appl. Math. , 20 (1967) pp. 329–363 -dimensional symmetric hyperbolic systems" Commun. Pure Appl. Math. , 20 (1967) pp. 329–363 |
| [a8] | J. Bazer, D.H.Y. Yen, "Lacunas of the Riemann matrix of symmetric-hyperbolic systems in two space variables" Commun. Pure Appl. Math. , 22 (1969) pp. 279–333 |
| [a9] | G.B. Folland, "Harmonic analysis in phase space" , Princeton Univ. Press (1989) |
| [a10] | R.P. Feynman, "An operator calculus having applications in quantum electrodynamics" Phys. Rev. , 84 (1951) pp. 108–128 |
| [a11] | H.J. Groenewold, "On the principles of elementary quantum mechanics" Physica , 12 (1946) pp. 405–460 |
| [a12] | M.J. Gotay, H.B. Grundling, G.M. Tuynman, "Obstruction results in quantization theory" J. Nonlinear Sci. , 6 (1996) pp. 469–498 |
| [a13] | L. Hörmander, "The Weyl calculus of pseudodifferential operators" Commun. Pure Appl. Math. , 32 (1979) pp. 359–443 |
| [a14] | L. Hörmander, "The analysis of linear partial differential operators" , III , Springer (1985) |
| [a15] | B. Jefferies, A. McIntosh, "The Weyl calculus and Clifford analysis" Bull. Austral. Math. Soc. , 57 (1998) pp. 329–341 |
| [a16] | J.J. Kohn, L. Nirenberg, "An algebra of pseudodifferential operators" Commun. Pure Appl. Math. , 18 (1965) pp. 269–305 |
| [a17] | V.P. Maslov, "Operational methods" , Mir (1976) |
| [a18] | J.E. Moyal, "Quantum mechanics as a statistical theory" Proc. Cambridge Philos. Soc. , 45 (1949) pp. 99–124 |
| [a19] | V.E. Nazaikinskii, V.E. Shatalov, B.Yu. Sternin, "Methods of noncommutative analysis" , Studies Math. , 22 , W. de Gruyter (1996) |
| [a20] | E. Nelson, "A functional calculus for non-commuting operators" F.E. Browder (ed.) , Functional Analysis and Related Fields: Proc. Conf. in Honor of Professor Marshal Stone (Univ. Chicago, May (1968) , Springer (1970) pp. 172–187 |
| [a21] | I. Petrovsky, "On the diffusion of waves and lacunas for hyperbolic equations" Mat. Sb. , 17 (1945) pp. 289–368 (In Russian) |
| [a22] | J.C.T. Pool, "Mathematical aspects of the Weyl correspondence" J. Math. Phys. , 7 (1966) pp. 66–76 |
| [a23] | M.E. Taylor, "Functions of several self-adjoint operators" Proc. Amer. Math. Soc. , 19 (1968) pp. 91–98 |
| [a24] | M.E. Taylor, "Pseudodifferential operators" , Princeton Univ. Press (1981) |
| [a25] | F. Treves, "Introduction to pseudodifferential and Fourier integral operators" , I , Plenum (1980) |
| [a26] | V.A. Vassiliev, "Ramified integrals, singularities and lacunas" , Kluwer Acad. Publ. (1995) |
| [a27] | H. Weyl, "The theory of groups and quantum mechanics" , Methuen (1931) (Reprint: Dover, 1950) |
Weyl calculus. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weyl_calculus&oldid=13545