Well-ordered set
A set 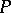 equipped with a binary relation
equipped with a binary relation  that satisfies the following conditions:
that satisfies the following conditions:
1) for any 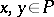 either
either 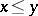 or
or 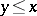 ;
;
2) if 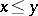 and
and  , then
, then 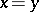 ;
;
3) if  and
and 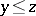 , then
, then 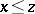 ;
;
4) in any non-empty subset 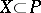 there exists an element
there exists an element  such that
such that 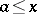 for all
for all 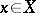 .
.
Thus, a well-ordered set is a totally ordered set satisfying the minimum condition.
The concept of a well-ordered set was introduced by G. Cantor [1]. An example of a well-ordered set is the naturally ordered set of natural numbers. On the other hand, the interval of real numbers 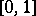 with the natural order is not well-ordered. Any subset of a well-ordered set is itself well-ordered. The Cartesian product of a finite number of well-ordered sets is well-ordered by the relation of lexicographic order. A totally ordered set is well-ordered if and only if it contains no subset which is anti-isomorphic to the set of natural numbers (cf. Anti-isomorphism of partially ordered sets).
with the natural order is not well-ordered. Any subset of a well-ordered set is itself well-ordered. The Cartesian product of a finite number of well-ordered sets is well-ordered by the relation of lexicographic order. A totally ordered set is well-ordered if and only if it contains no subset which is anti-isomorphic to the set of natural numbers (cf. Anti-isomorphism of partially ordered sets).
The smallest element of a well-ordered set 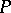 is denoted by zero (the symbol 0). For any element
is denoted by zero (the symbol 0). For any element 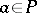 , the set
, the set
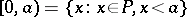 |
is called an initial segment of  . For any element
. For any element  which is not the largest element in
which is not the largest element in 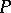 there exists an element immediately following it; it is usually denoted by
there exists an element immediately following it; it is usually denoted by 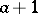 . An element of a well-ordered set which has no element immediately preceding it is called a limit element.
. An element of a well-ordered set which has no element immediately preceding it is called a limit element.
The comparison theorem. For any two well-ordered sets 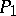 and
and 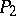 one and only one of the following situations occurs: a)
one and only one of the following situations occurs: a) 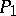 is isomorphic to
is isomorphic to  ; b)
; b) 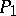 is isomorphic to an initial segment of
is isomorphic to an initial segment of 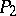 ; or c)
; or c) 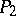 is isomorphic to an initial segment of
is isomorphic to an initial segment of 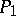 .
.
If the axiom of choice is included in the axioms of set theory, it may be shown that it is possible to impose on any non-empty set an order relation which converts it into a well-ordered set (i.e. any non-empty set can be well-ordered). This theorem, known as the Zermelo theorem, is in fact equivalent to the axiom of choice. Zermelo's theorem and the comparison theorem form the basis for the comparison between cardinalities of sets. Order types of well-ordered sets are called ordinal numbers (cf. Order type; Ordinal number).
References
| [1] | G. Cantor, "Über unendliche, lineaire Punktmannigfaltigkeiten" Math. Ann. , 21 (1883) pp. 51–58 |
| [2] | P.S. Aleksandrov, "Einführung in die Mengenlehre und die Theorie der reellen Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian) |
| [3] | F. Hausdorff, "Grundzüge der Mengenlehre" , Leipzig (1914) (Reprinted (incomplete) English translation: Set theory, Chelsea (1978)) |
| [4] | N. Bourbaki, "Elements of mathematics. Theory of sets" , Addison-Wesley (1968) (Translated from French) |
| [5] | K. Kuratowski, A. Mostowski, "Set theory" , North-Holland (1968) |
Comments
In the definition above, condition 3) (the transitivity of the order relation) is in fact redundant: it follows from the existence of a least element in the subset 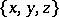 .
.
Sometimes a well-ordered set is called a totally well-ordered set, reflecting the fact that the ordering is a total ordering or linear ordering. Cf. Totally ordered set.
References
| [a1] | A. Levy, "Basic set theory" , Springer (1979) |
Well-ordered set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Well-ordered_set&oldid=12987