Weight of a representation of a Lie algebra
in a vector space 
A linear mapping 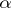 from the Lie algebra
from the Lie algebra 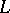 into its field of definition
into its field of definition 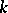 for which there exists a non-zero vector
for which there exists a non-zero vector  of
of 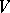 such that for the representation
such that for the representation 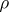 one has
one has
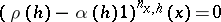 |
for all  and some integer
and some integer 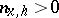 (which in general depends on
(which in general depends on  and
and  ). Here 1 denotes the identity transformation of
). Here 1 denotes the identity transformation of 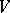 . One also says in such a case that
. One also says in such a case that 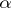 is a weight of the
is a weight of the  -module
-module 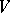 defined by the representation
defined by the representation 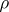 . The set of all vectors
. The set of all vectors 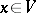 which satisfy this condition, together with zero, forms a subspace
which satisfy this condition, together with zero, forms a subspace 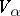 , which is known as the weight subspace of the weight
, which is known as the weight subspace of the weight 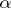 (or corresponding to
(or corresponding to 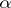 ). If
). If  , then
, then 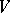 is said to be a weight space or weight module over
is said to be a weight space or weight module over 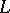 of weight
of weight 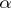 .
.
If 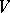 is a finite-dimensional module over
is a finite-dimensional module over 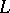 of weight
of weight 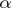 , its contragredient module (cf. Contragredient representation)
, its contragredient module (cf. Contragredient representation) 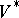 is a weight module of weight
is a weight module of weight 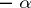 ; if
; if 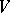 and
and 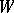 are weight modules over
are weight modules over 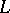 of weights
of weights 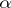 and
and 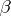 , respectively, then their tensor product
, respectively, then their tensor product 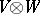 is a weight module of weight
is a weight module of weight 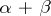 . If
. If 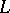 is a nilpotent Lie algebra, a weight subspace
is a nilpotent Lie algebra, a weight subspace 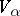 of weight
of weight 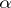 in
in 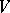 is an
is an 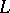 -submodule of the
-submodule of the 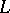 -module
-module 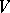 . If, in addition,
. If, in addition,
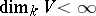 |
and 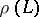 is a splitting Lie algebra of linear transformations of the module
is a splitting Lie algebra of linear transformations of the module 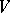 , then
, then 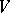 can be decomposed into a direct sum of a finite number of weight subspaces of different weights:
can be decomposed into a direct sum of a finite number of weight subspaces of different weights:
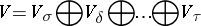 |
(the weight decomposition of 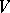 with respect to
with respect to 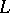 ). If
). If 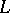 is a nilpotent subalgebra of a finite-dimensional Lie algebra
is a nilpotent subalgebra of a finite-dimensional Lie algebra 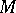 , considered as an
, considered as an 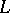 -module with respect to the adjoint representation
-module with respect to the adjoint representation 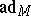 of
of 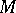 (cf. Adjoint representation of a Lie group), and
(cf. Adjoint representation of a Lie group), and  is a splitting Lie algebra of linear transformations of
is a splitting Lie algebra of linear transformations of 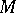 , then the corresponding weight decomposition of
, then the corresponding weight decomposition of 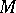 with respect to
with respect to  ,
,
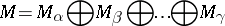 |
is called the Fitting decomposition of 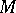 with respect to
with respect to  , the weights
, the weights 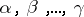 are called the roots, while the spaces
are called the roots, while the spaces 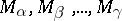 are called the root subspaces of
are called the root subspaces of 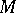 with respect to
with respect to 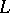 . If, in addition, one specifies the representation
. If, in addition, one specifies the representation  of the algebra
of the algebra 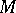 in a finite-dimensional vector space
in a finite-dimensional vector space 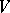 for which
for which 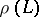 is a splitting Lie algebra of linear transformations of
is a splitting Lie algebra of linear transformations of 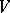 , and
, and
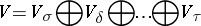 |
is the corresponding weight decomposition of 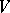 with respect to
with respect to 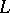 , then
, then 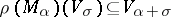 if
if 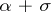 is a weight of
is a weight of 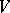 with respect to
with respect to 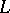 , and
, and 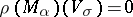 otherwise. In particular, if
otherwise. In particular, if 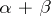 is a root, then
is a root, then 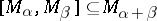 , and
, and 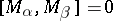 otherwise. If
otherwise. If 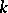 is a field of characteristic zero, the weights
is a field of characteristic zero, the weights  and the roots
and the roots 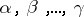 are linear functions on
are linear functions on 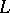 which vanish on the commutator subalgebra of
which vanish on the commutator subalgebra of 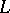 .
.
References
| [1] | N. Jacobson, "Lie algebras" , Interscience (1962) ((also: Dover, reprint, 1979)) |
| [2] | D.P. Zhelobenko, "Compact Lie groups and their representations" , Amer. Math. Soc. (1973) (Translated from Russian) |
Comments
A set (algebra, Lie algebra, etc.) 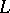 of linear transformations of a vector space over a field
of linear transformations of a vector space over a field 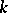 is called split or splitting if the characteristic polynomial of each of the transformations has all its roots in
is called split or splitting if the characteristic polynomial of each of the transformations has all its roots in 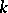 , i.e. if
, i.e. if 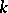 contains a splitting field (cf. Splitting field of a polynomial) of the characteristic polynomial of each
contains a splitting field (cf. Splitting field of a polynomial) of the characteristic polynomial of each 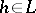 .
.
A representation  of Lie algebras is split if
of Lie algebras is split if 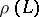 is a split Lie algebra of linear transformations.
is a split Lie algebra of linear transformations.
References
| [a1] | N. Bourbaki, "Groupes et algèbres de Lie" , Hermann (1975) pp. Chapts. VII-VIII |
Weight of a representation of a Lie algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weight_of_a_representation_of_a_Lie_algebra&oldid=17874