Weierstrass criterion (for uniform convergence)
A theorem which gives sufficient conditions for the uniform convergence of a series or sequence of functions by comparing them with appropriate series and sequences of numbers; established by K. Weierstrass . If, for the series
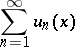 |
of real- or complex-valued functions defined on some set 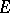 there exists a convergent series of non-negative numbers
there exists a convergent series of non-negative numbers
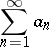 |
such that
 |
then the initial series converges uniformly and absolutely on the set  (cf. Absolutely convergent series). For instance, the series
(cf. Absolutely convergent series). For instance, the series
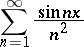 |
converges uniformly and absolutely on the entire real axis, since
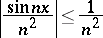 |
and the series
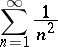 |
is convergent.
If, for a sequence of real- or complex-valued functions 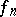 ,
, 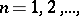 which converges to a function
which converges to a function  on a set
on a set 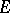 there exists a sequence of numbers
there exists a sequence of numbers 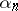 ,
,  and
and 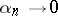 as
as 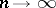 , such that
, such that  ,
, 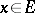 ,
, 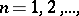 then the sequence converges uniformly on
then the sequence converges uniformly on 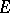 . For instance, the sequence
. For instance, the sequence
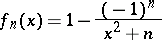 |
converges uniformly to the function 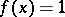 on the entire real axis, since
on the entire real axis, since
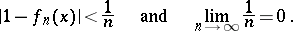 |
The Weierstrass criterion for uniform convergence may also be applied to functions with values in normed linear spaces.
References
| [1a] | K. Weierstrass, "Abhandlungen aus der Funktionenlehre" , Springer (1866) |
| [1b] | K. Weierstrass, "Math. Werke" , 1–7 , G. Olms & Johnson, reprint (1927) |
Comments
References
| [a1] | T.M. Apostol, "Mathematical analysis" , Addison-Wesley (1974) |
| [a2] | K. Knopp, "Theorie und Anwendung der unendlichen Reihen" , Springer (1964) (English translation: Blackie, 1951 & Dover, reprint, 1990) |
| [a3] | W. Rudin, "Real and complex analysis" , McGraw-Hill (1974) pp. 24 |
Weierstrass criterion (for uniform convergence). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weierstrass_criterion_(for_uniform_convergence)&oldid=19294