Wedderburn-Artin theorem
From Encyclopedia of Mathematics
A theorem which fully describes the structure of associative Artinian rings (cf. Artinian ring) without nilpotent ideals. An associative ring 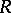 (cf. Associative rings and algebras) has the minimum condition for right ideals and has no nilpotent ideals if and only if
(cf. Associative rings and algebras) has the minimum condition for right ideals and has no nilpotent ideals if and only if 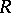 is the direct sum of a finite number of ideals, each of which is isomorphic to a complete ring of matrices of finite order over a suitable skew-field; this decomposition into a direct sum is unique apart from the ordering of its terms. This theorem was first obtained by J. Wedderburn for finite-dimensional algebras over a field, and was proved by E. Artin [1] in its final formulation.
is the direct sum of a finite number of ideals, each of which is isomorphic to a complete ring of matrices of finite order over a suitable skew-field; this decomposition into a direct sum is unique apart from the ordering of its terms. This theorem was first obtained by J. Wedderburn for finite-dimensional algebras over a field, and was proved by E. Artin [1] in its final formulation.
References
| [1] | E. Artin, "The influence of J.H.M. Wedderburn on the development of modern algebra" Bull. Amer. Math. Soc. , 56 (1950) pp. 65–72 |
Comments
References
| [a1] | J.H.M. Wedderburn, "Lectures on matrices" , Dover, reprint (1964) |
| [a2] | C. Faith, "Algebra: rings, modules, and categories" , 1 , Springer (1973) pp. 380, 369 |
| [a3] | P.M. Cohn, "Algebra" , 2 , Wiley (1989) pp. 174ff |
How to Cite This Entry:
Wedderburn-Artin theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Wedderburn-Artin_theorem&oldid=18489
Wedderburn-Artin theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Wedderburn-Artin_theorem&oldid=18489
This article was adapted from an original article by K.A. Zhevlakov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article