Weber problem
A problem formulated in [a7] as a model for the optimum location of a facility in the plane intended to serve several users; for example, a central source of electric power. One is seeking the minimum of a function
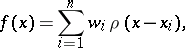 |
where the  are positive scalars, the
are positive scalars, the  are given vectors in
are given vectors in  ,
,  is in
is in  and
and  is the Euclidean norm of
is the Euclidean norm of  . The case when all
. The case when all  and
and 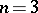 had been considered by P. Fermat in 1629, by E. Torricelli in 1644 and by J. Steiner in 1837. (For the early history of the problem, see [a4].)
had been considered by P. Fermat in 1629, by E. Torricelli in 1644 and by J. Steiner in 1837. (For the early history of the problem, see [a4].)
The function 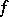 is convex (cf. Convex function (of a real variable)) and one shows that, with some exceptions, it has a unique minimizer. These assertions remain valid when
is convex (cf. Convex function (of a real variable)) and one shows that, with some exceptions, it has a unique minimizer. These assertions remain valid when 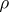 is allowed to be an arbitrary norm and
is allowed to be an arbitrary norm and 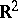 is replaced by
is replaced by  .
.
For applications, of which there are many (see [a1]), one seeks good computational methods for finding a minimizer of  , either with the Euclidean norm or with other norms. For the Euclidean case, E. Weiszfeld [a8] provided a much used method; see [a6] for a discussion of this and other cases. If
, either with the Euclidean norm or with other norms. For the Euclidean case, E. Weiszfeld [a8] provided a much used method; see [a6] for a discussion of this and other cases. If  is the
is the  -norm, explicit solution is possible (see [a2], Chap. 4).
-norm, explicit solution is possible (see [a2], Chap. 4).
Minimizing the function 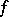 is a problem in optimization and it is natural to seek a dual problem (cf. Duality in extremal problems and convex analysis): to maximize a function
is a problem in optimization and it is natural to seek a dual problem (cf. Duality in extremal problems and convex analysis): to maximize a function 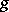 such that
such that 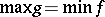 . A dual was found for special cases by H.W. Kuhn and others [a4]. A major result in this direction was provided by C. Witzgall in [a9], who provided a dual for a more general minimum problem, in which the function to be minimized has the form
. A dual was found for special cases by H.W. Kuhn and others [a4]. A major result in this direction was provided by C. Witzgall in [a9], who provided a dual for a more general minimum problem, in which the function to be minimized has the form
 |
where 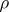 is now allowed to be an asymmetric norm in
is now allowed to be an asymmetric norm in 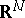 (that is,
(that is, 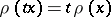 is required to be valid only for non-negative
is required to be valid only for non-negative 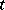 ) and
) and  . Witzgall's result and others are subsumed under a duality theorem of W. Kaplan and W.H. Yang [a3]. In this theorem, the function
. Witzgall's result and others are subsumed under a duality theorem of W. Kaplan and W.H. Yang [a3]. In this theorem, the function 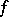 has the form
has the form
 |
in  , where
, where 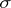 is a norm, allowed to be asymmetric, in
is a norm, allowed to be asymmetric, in  ,
, 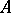 is a constant
is a constant 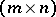 -matrix,
-matrix,  in
in  and
and  in
in  are constant vectors. The dual function
are constant vectors. The dual function 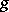 is the linear function
is the linear function 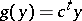 in
in  , subject to the constraints
, subject to the constraints  and
and 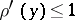 , where
, where 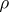 and
and  are dual norms in
are dual norms in  :
: 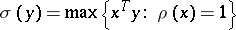 . It is assumed that the equation
. It is assumed that the equation  has a solution with
has a solution with 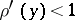 . In [a3] it is shown how, when the norms are differentiable (except at the origin), a minimizer of
. In [a3] it is shown how, when the norms are differentiable (except at the origin), a minimizer of  can be obtained from or determines a maximizer of
can be obtained from or determines a maximizer of  . It is also shown that the theorem provides a dual for the multi-facility location problem, for which the function
. It is also shown that the theorem provides a dual for the multi-facility location problem, for which the function 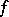 to be minimized is the sum of the weighted distances from
to be minimized is the sum of the weighted distances from 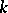 new facilities to
new facilities to  given facilities as well as the weighted distances between the new facilities; the function
given facilities as well as the weighted distances between the new facilities; the function  is a convex function of
is a convex function of  , where the
, where the  th new facility is placed at
th new facility is placed at 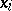 .
.
The Weber problem has been generalized in many ways to fit the great variety of problems arising in the location of facilities. See [a1] for an overview.
References
| [a1] | Z. Drezner, "Facility location, a survey of applications and methods" , Springer (1995) |
| [a2] | R.L. Francis, J.A. White, "Facility layout and location: an analytical approach" , Prentice-Hall (1974) |
| [a3] | W. Kaplan, W.H. Yang, "Duality theorem for a generalized Fermat–Weber problem" Math. Progr. , 7 : 6 (1997) pp. 285–297 |
| [a4] | H.W. Kuhn, "On a pair of dual nonlinear programs" J. Abadie (ed.) , Nonlinear programming , Wiley (1967) pp. 39–54 |
| [a5] | R.F. Love, J.G. Morris, G.O. Wesolovsky, "Facilities location, models and methods" , North-Holland (1988) |
| [a6] | F. Plastria, "Continuous location problems" Z. Drezner (ed.) , Facility location, a survey of applications and methods , Springer (1995) pp. 225–262 |
| [a7] | A. Weber, "Theory of the location of industries" , Univ. Chicago Press (1957) (Translated from German) |
| [a8] | E. Weiszfeld, "Sur le point lequel la somme des distances de  points donnés est minimum" Tôhoku Math. J. , 43 (1937) pp. 355–386 points donnés est minimum" Tôhoku Math. J. , 43 (1937) pp. 355–386 |
| [a9] | C. Witzgall, "Optimal location of a central facility: mathematical models and concepts" Nat. Bureau Standards Report , 8388 (1964) |
Weber problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weber_problem&oldid=16979