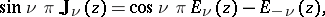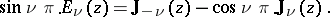The function
where  is a complex number and
is a complex number and  is a real number. It satisfies the inhomogeneous Bessel equation
is a real number. It satisfies the inhomogeneous Bessel equation
For non-integral  the following expansion is valid:
the following expansion is valid:
If 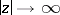 and
and  , the following asymptotic expansion is valid:
, the following asymptotic expansion is valid:
where 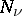 is the Neumann function. If
is the Neumann function. If  is not an integer, the Weber function is related to the Anger function
is not an integer, the Weber function is related to the Anger function 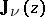 by the following equations:
by the following equations:
The Weber functions were first studied by H. Weber [1].
References
| [1] | H.F. Weber, Zurich Vierteljahresschrift , 24 (1879) pp. 33–76 |
| [2] | G.N. Watson, "A treatise on the theory of Bessel functions" , 1 , Cambridge Univ. Press (1952) |
How to Cite This Entry:
Weber function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weber_function&oldid=13892
This article was adapted from an original article by A.P. Prudnikov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article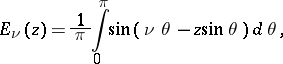
 is a complex number and
is a complex number and  is a real number. It satisfies the inhomogeneous Bessel equation
is a real number. It satisfies the inhomogeneous Bessel equation
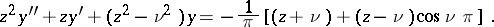
 the following expansion is valid:
the following expansion is valid:

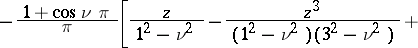
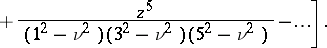
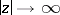 and
and  , the following asymptotic expansion is valid:
, the following asymptotic expansion is valid:
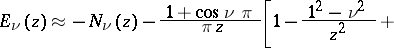
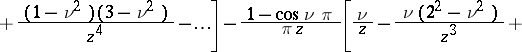
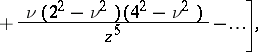
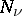 is the Neumann function. If
is the Neumann function. If  is not an integer, the Weber function is related to the Anger function
is not an integer, the Weber function is related to the Anger function 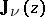 by the following equations:
by the following equations: