Weak solution

of a differential equation

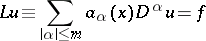in a domain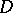

A locally integrable function satisfying the equation

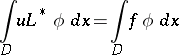for all smooth functions 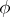(say, of class ) with compact support in . Here, the coefficients in

are assumed to be sufficiently smooth and 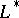stands for the formal Lagrange adjoint of :

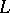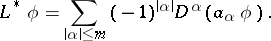For example, the generalized derivative 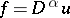can be defined as the locally integrable function 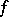such that is a weak solution of the equation .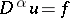

In considering weak solutions of , the following problem arises: under what conditions are they strong solutions (cf. Strong solution)? For example, in the case of elliptic equations, every weak solution is strong.

References

[1]	A.V. Bitsadze, "Some classes of partial differential equations" , Gordon & Breach (1988) (Translated from Russian)

References

[a1]	S. Agmon, "Lectures on elliptic boundary value problems" , v. Nostrand (1965)
[a3]	D. Gilbarg, N.S. Trudinger, "Elliptic partial differential equations of second order" , Springer (1983)